Hey all!
We would like to invite you all to an online replay contest for UWCOI 2020. UWCOI 2020 is an OI-style contest hosted by UWCSEA Dover which was used to select members for the UWCSEA Dover team for the Singapore National Olympiad in Informatics for this year. The online replay contest will be held as a round rated for both Divisions on CodeChef.
Here are some details:
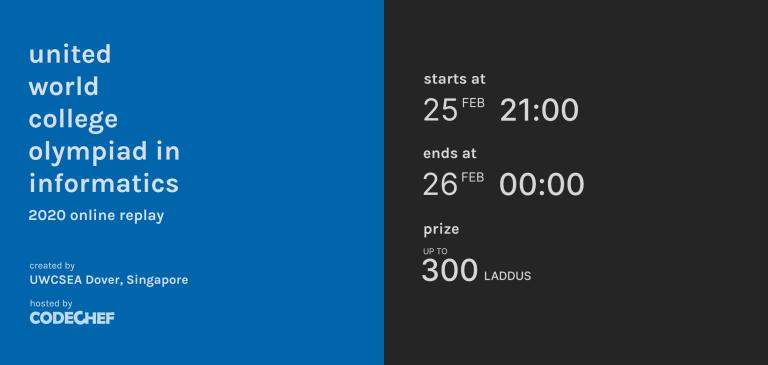
- Time: Tuesday, February 25, 2020, 21:00 hrs IST (Indian Standard Time). Please check your local timezone here.
- Contest Format: 7 OI-style tasks (all tasks have subtasks) in 3 hours
- There is no time penalty for non-accepted verdicts; however, time will be used as the tiebreak.
- The contest is rated for both divisions (all ratings).
- The writers are astoria, kimbj0709 and socho.
- The technical committee also includes smjleo.
- The contest is hosted on CodeChef, at this link.
- For all questions, please email us at [email protected]
We hope you enjoy the contest!
Update: Just a gentle reminder that the contest begins in about 3 hours from now! We hope to see you there!
Update 2:
Thank you all for participating! We hope you enjoyed the contest. Here are the problems and editorials:
- A: Peak Finding by astoria — Problem Link — Editorial Link.
- B: Button Pairs by socho — Problem Link — Editorial Link.
- C: Mercury Poisoning by astoria — Problem Link — Editorial Link.
- D: Base Plans by socho — Problem Link — Editorial Link.
- E: Escape by kimbj0709 — Problem Link — Editorial Link.
- F: Blocks by socho — Problem Link — Editorial Link.
- G: Optimal Memory Address by astoria — Problem Link — Editorial Link
Please let us know if you have any comments / feedback!
Update 3: All editorials are now available!
Thanks,
The UWCOI Committee











7 questions with subtasks in 3 hours :o
errorgorn orz
shenxy13 orz
bensonlzl orz
Nice problemset.
problemset was good but most unbalanced contest i have ever given.
most unbalanced, what? Haven't you ever participated in Codechef Cook-offs and Lunchtime.
Yes i gave codechef short contest after very long time
Can't agree. Very well balanced contest with cool problems wisely divided on subtasks.
How to solve Mercury Poisoning?
Process queries offline. Then you can count number of reachable cells using ufds.
I thought about this, To sort the queries in the ascending order of powers and solve them in order. When we reach a cell which is already visited due to a previous query, add the size of that set to the answer and combine the present set of cells to that set using ufds.
But, there could be some cells(A[i][j] > Power(previous query) but A[i][j] < Power(current query)) which are reachable from already visited(from previous queries) cells but are not directly reachable just through unvisited cells from the current starting cell, right? How did you take care of that? I hope my question is clear...
Maintain another vector of cells and sort them by power. When you process a new query you process cells that are newly reachable.
Idk if theres a faster method... my code got 1.9s
I did exactly this. I also converted the grid into linear n*m array and carried out the union find operations. But it is not passing the TL on last subtask. Can you catch the bug here
Just use vector pair and sort them instead of using map. It will work smoothly. Bcz simply inserting random 1e6 elements into the map takes almost a second, more precisely 0.91 as measured on ideone by me. You are doing it for 2 test cases + dsu + map with vector is also a bit slow (arrays are faster than vector).
You need to sort both the queries and the matrix(in a temporary array) and process them using two pointers and join matrix elements using DSU while checking appropriate conditions.
What is udfs?
Union-disjoint find set
I read it udfs in place of ufds which is why I got confused. But you then also changed the abbreviation to make it Union-disjoint find set? haha xD
Is there a more elegant method for Escape than running O(K) dijkstra to compress the graph?
Not that I know of.
sadly the following method didn't work (and don't know why):
do a multi-source dijkstra from all important nodes, and save for every node in the graph the closest important node to it, and then build the new graph from the edges that have ends closest to different important nodes.
for more details about this method please see F. Cheap Robot Editorial.
I think because cheap robot you only care about the nearest imporant node. But here we cannot just ignore that. Suppose A,B and C are all keys.
You have edge from AB and BC.
Suppose A-D and D-C is very long, you will only have edge from A-B and B-C in your new graph, so now when you find the weight of A-C, it will be the length of (A-C) + (D-B)*2.
But not entirely sure as maybe your implementation may be different. maybe i can look at your code?
yes you're right, sometimes in the compressed graph we can't reach some key nodes which we actually can reach in the original graph, so the solution is wrong.
here is a simple counter-test:
5 4 1
1 2 1000
2 3 1000
2 4 1
4 5 1
3 4
answer: 3002
my output: -1
node $$$4$$$ is locked and the key is in node $$$3$$$.
after running the multi-source dijkstra and labeling the graph nodes by the nearest important node, the graph will look like this:
1 4 1000
4 3 1000
4 4 1
4 5 1
(node $$$4$$$ is the nearest to node $$$2$$$, so we replace the $$$2$$$ by $$$4$$$)
and the compressed graph:
1 4 1001
4 3 1001
4 5 1
so now we can't get the key from node $$$3$$$ before visiting node $$$4$$$.
thanks for debugging the idea, and here is my code.
Can you please elaborate on the approach you had
How to solve Blocks?
240 = maximum number of divisors of number less than million. Iterate over divisors, how to check whether some number $$$k$$$ can be answer? It is easy to see that answer for query $$$n / k$$$ should be $$$n$$$ — $$$n/k$$$. Then to solve a problem fully you need to iterate over prime divisors of $$$n$$$, and use the fact that if some number $$$k$$$ can't be an answer, than no number divisible by $$$k$$$ can't be an answer too.
For $$$Q \le 240$$$, simply brute-force all the factors of $$$N$$$.
For $$$Q \le 20$$$, factorize $$$N$$$ as $$${p_1}^{k_1}{p_2}^{k_2}\dots {p_n}^{k_n}$$$. Since $$$2^{20} > 10^6$$$, it is enough to make queries for each $$$\frac{N}{{p_i}^{k_i}}$$$.
For $$$Q \le 9$$$, use binary search to the power of each prime factor.
1st two problems was very easy but after those two difficulty gap was huge! Problems difficulty should be balanced for a good contest :/
There were subtasks, didn't you see?
Please provide some tutorial ,question link of counting problems