Hello everyone! I invented function F(x):{2,3,...}->N: if x is simple, F(x) is equal to its number in the sequence of prime numbers, if x is composite, F(x) is equal to its number in sequence of composite numbers. It is obvious that for any positive integer after a few uses of this function we will get 1. For example: F(22)=13, F(13)=6, F(6)=2, F(2)=1.
Now let's build an infinite binary tree: in the root is the number 1, for each vertex, which contains number N left son is N-th prime number and right son is N-th composite number. We'll get something like this: 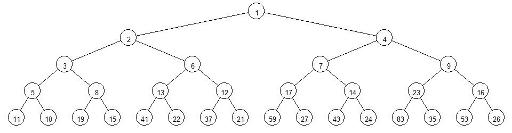 This tree has the following properties:
This tree has the following properties:
- It contains all positive integers;
- Parent of vertex with number N is F(N);
- For each vertex the path from it to the root is a sequence of numbers generated by repeated calculation of the function F(x).
I don't know whether it might have some use, but it seems to me that it is not without a certain beauty. Besides, this, the same tree can be constructed in any two disjoint sets that their union is the set of natural numbers except 1 (if one of sets contains the number 1, almost nothing will change, just there will be loop from the root in himself, but it will not be a tree).











Oh man, why on earth would you use two negatives (..not without..) and hinder me understanding things XD.
Soo, I got to use my algorithm to change that sentence into a one I can understand.
So, removing both of negatives from there. Hm...
"...but it seems to me that it is with a certain beauty.." !!!!
I am awesome : D
OK. to the point, you too are awesome xD