So I was looking through my WA verdict on today's Educational Round Problem C. It failed on the following case, 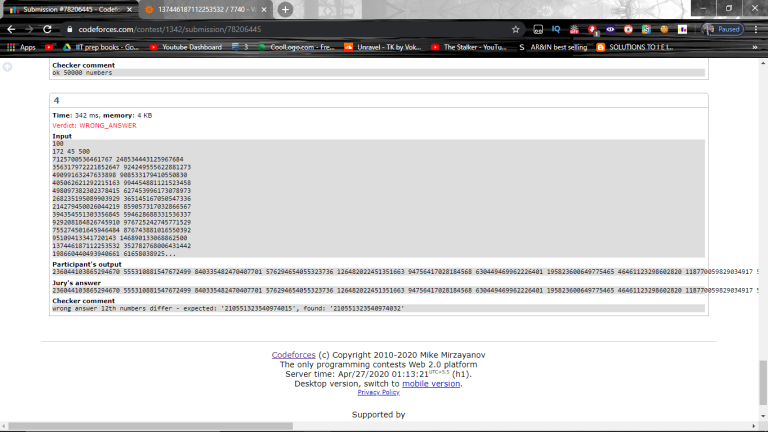
But when I run the test locally for the first 12 queries (couldnt access the full test case), It gives the expected output.
Submission : https://codeforces.com/contest/1342/submission/78206445
What is the problem here? I don't quite get it. Thanks for the help :)










run your code with "Clang++17 Diagnostics". this compiler will found a bug
Same code on submitting with C++17 gets accepted. Funnily enough, I use C++14 locally.
CLANG C++ DIAGNOSTICS! it is not simple c++17 compiler. clang can found some mistakes such as RE (division by 0, out of bounds array etc). I try to run your code with it and it found a mistake. you can find this compiler on codeforces (problemset->custom test, then choose this compiler and run with a sample) it will found a mistake and give you a report
I understand that but how can just changing language version change WA to AC? Try to submit my code with C++17 (GNU)
On the 12th query, the
floor((db)r/(db)lcm) == (db)r/(db)lcmstatement evaluates to true in C++14 and false in C++17. I assume that some change in C++17 changed floating point arithmetic.In general, just avoid using floating point if possible. They're painful to debug and not consistent on different compilers. This problem can be solved without floating point, so if you want you can try rewriting your solution again with that strategy. I personally would rather not have the correctness of my code depend on the compiler I'm using.
But it gives expected output even with C++14 when testing locally.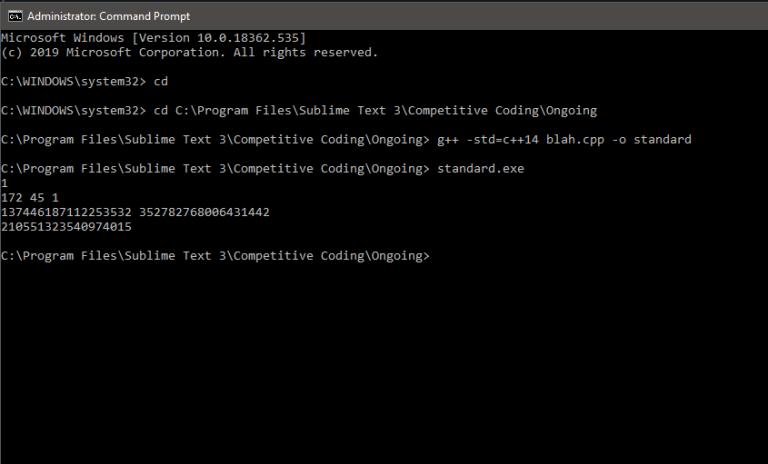
Also can you share your approach for the problem? I tried to look at your code but I don't get it.
My solution splits the query into x blocks of size a*b, with one (potentially empty) block left over.
The answer for each block is the same, and can be calculated in O(A*B) time by iterating through from 0 to a*b and checking if (i % a) % b == (i % b) % a. I don't know how to rigorously prove this, but it's probably in the editorial.
Then for the last partial block, the answer can be calculated with a prefix sum that was calculated beforehand. Many solutions got hacked with TLE because they didn't calculate the prefix sum for the partial block.
So we have
sum[i]which holds the count of numbers that meet the condition in the problem from 0 to i. For each full block we addsum[a*b - 1], and then for the last block addsum[M % (a*b)]whereMis the size of the query you're trying to solve.Also, for simplicity, each query with
L, Ris converted intoans(R) - ans(L-1)to ensure that the blocks line up.Some solutions used
lcd(a, b)instead ofa*b, and they're faster than mine. But both should pass.You should probably read the actual editorial as well. It will almost certainly make more sense than what I just wrote.
No, it does make perfect sense. I actually wrote a brute force solution and noticed a pattern that (i % a) % b == (i % b) % a only when i lies in the range [ n*LCM , n*LCM + max(a,b) ) where n is any integer and I am counting such blocks in my answer.
I submitted a solution 78241725 that failed on the 48405th query of test case 2. Instead of precalculating all numbers from 0 to a*b, and then using the periodic property of that, I used this idea.
(i%a)%b will be equal to (i%b)%a for all i from l to b (l included, b excluded)
For every b numbers after i (i included), where i%lcm==0, the value of (i%a)%b will be equal to (i%b)%a.
I computed this count, taking care of left and right limits, but funnily enough my testcase 2 failed at 48405th query, seems some corner case is missing.Any help will be appreciated. PS. I managed to solve the way you did later after the contest, and it worked.