My roommates and me are planning a house party. Because of covid, the Dutch rules says that we can have a party as long as social distancing is maintained — each individual has to be at least 1.5m away from each other. This brings me to a cool real life problem — what is the minimum area required to fit N people such that each one maintains social distancing with everyone else. N > 2, since we are already 3 roommates :)
My guessed solution is to make everyone stand on the vertices of equilateral triangle, and then join these triangles to form hexagonal lattice (just like a cellular network). Hence the answer would be (N — 2) * area of equilateral triangle of side 1.5m. Is this correct?
If yes, a follow up question would be : What if I wanted to minimise the distance between the farthest people as well? Would I try to fit these triangles inside a square?
Will be nice to hear out solutions to both these problems, for any number of people (N).
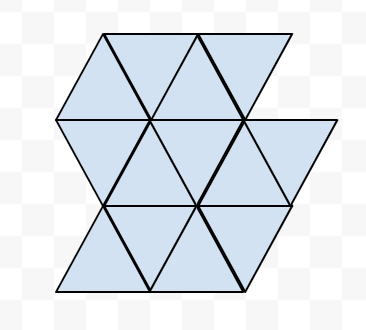











Your problem is equivalent to arranging disjoint circles of radius $$$X/2$$$ (where $$$X$$$ is the distance requirement). Your solution corresponds to "hexagonal packing" and is indeed optimal for big areas. Read more about circle packing: https://mathworld.wolfram.com/CirclePacking.html
Thanks. Would it also work in case I want to minmize the distance between the farthest two people? What would be the area in that case?
Hey can you provide me the solution for this question?