1428A - Box is Pull
Setter: bensonlzl
Prepared by: errorgorn
Consider when $$$x_1=x_2$$$
Consider when $$$x_1 \ne x_2$$$
We consider 2 cases.
The first is that the starting and ending point lie on an axis-aligned line. In this case, we simply pull the box in 1 direction, and the time needed is the distance between the 2 points as we need 1 second to decrease the distance by 1.
The second is that they do not lie on any axis-aligned line. Wabbit can pull the box horizontally (left or right depends on the relative values of $$$x_1$$$ and $$$x_2$$$) for $$$|x_1-x_2|$$$ seconds, take 2 seconds to move either above or below the box, then take another $$$|y_1-y_2|$$$ seconds to move the box to $$$(x_2,y_2)$$$.
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
int t, x1, y1, x2, y2;
cin >> t;
for (int i = 1; i <= t; ++i){
cin >> x1 >> y1 >> x2 >> y2;
if (x1 == x2 || y1 == y2){
cout << abs(x1-x2) + abs(y1-y2) << '\n';
}
else cout << abs(x1-x2) + abs(y1-y2) + 2 << '\n';
}
}
tc=int(input())
for i in range(tc):
a,b,c,d=map(int,input().split(" "))
ans=abs(a-c)+abs(b-d)
if (a!=c and b!=d): ans+=2
print(ans)
1428B - Belted Rooms
Setter: oolimry
Prepared by: oolimry
There are 2 cases to consider for a room to be returnable.
For a room to be returnable, either go one big round around all the rooms or move to an adjacent room and move back.
Let's consider two ways to return to the start point. The first is to go one big round around the circle. The second is to move 1 step to the side, and return back immediately.
Going one big round is only possible if and only if:
- There are no clockwise belts OR
- There are no anticlockwise belts
If we can go one big round, all rooms are returnable.
If there are both clockwise and anticlockwise belts, then we can't go one big round. For any room to be returnable, it must have an off belt to the left or to the right.
In summary, check if clockwise belts are absent or if anticlockwise belts are absent. If either is absent, the answer is $$$n$$$. Otherwise, we have to count the number of rooms with an off belt to the left or to the right.
Sorry for the unclear statement for B, we should've explained each sample testcase more clearly with better diagrams. Additionally, we're also sorry for the weak pretests. We should've added more testcases of smaller length, and thanks to hackers for adding stronger tests.
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
int TC; cin >> TC;
while(TC--){
int n; cin >> n;
string s; cin >> s;
bool hasCW = false;
bool hasCCW = false;
for(int i = 0;i < n;i++){
if(s[i] == '<') hasCW = true;
if(s[i] == '>') hasCCW = true;
}
if(hasCW && hasCCW){
int ans = 0;
s += s[0];
for(int i = 0;i < n;i++){
if(s[i] == '-' || s[i+1] == '-') ans++;
}
cout << ans << "\n";
}
else{
cout << n << "\n";
}
}
}
TC = int(input())
for tc in range(TC):
n = int(input())
s = input()
hasCW = False
hasCCW = False
for c in s:
if c == '>':
hasCW = True
if c == '<':
hasCCW = True
if hasCW and hasCCW:
s += s[0]
ans = 0;
for i in range(n):
if s[i] == '-' or s[i+1] == '-':
ans += 1
print(ans)
else:
print(n)
1428C - ABBB
Setter: errorgorn and shenxy13
Prepared by: errorgorn and oolimry
AB and BB means that ?B can be removed.
The final string is BAAA... or AAA....
This game is equivalent to processing left to right and maintaining a stack. If the current processed character is A, we add it to the stack, if the current processed character is B, we can either add it to the stack or pop the top of the stack.
In the optimal solution, we will always pop from the stack whenever possible. To prove this, we will use the stay ahead argument.
Firstly, we notice that the contents of the stack do not actually matter. We actually only need to maintain the length of this stack. Decrementing the size of the stack whenever possible is optimal as it is the best we can do. And in the case where we must push `B' to the stack, this is optimal as the parity of the length of the stack must be the same as the parity of the processed string, so obtaining a stack of length 0 is impossble.
Bonus: what is the length of the longest string that Zookeeper can make such that there are no moves left?
We're also sorry for the weak pretests in this problem. About 1 hour before the contest, we found out that c++ $$$O(N^2)$$$ solution using find and erase would pass. Then we added testcases to kill the c++ solutions, but we didn't test the $$$O(N^2)$$$ solution for python using replace.
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
string s;
cin>>s;
int stk=0;
rep(x,0,sz(s)){
if (stk && s[x]=='B') stk--;
else stk++;
}
cout<<stk<<endl;
}
}
TC = int(input())
for tc in range(TC):
s = input()
ans=0
for i in s:
if (i=='B' and ans!=0): ans-=1
else: ans+=1
print(ans)
1428D - Bouncing Boomerangs
Setter: bensonlzl
Prepared by: bensonlzl
Consider $$$a_i \in \{0,1,2\}$$$.
Consider $$$a_i=\{3,3,3, \ldots , 3,1\}$$$.
Clearly, columns with $$$a_j=0$$$ are completely empty and we can ignore them.
Let's first consider just columns with $$$1$$$ s and $$$2$$$ s. When a boomerang strikes its first target, it will change directions from upwards to rightwards. If $$$a_j=1$$$, the boomerang in column $$$j$$$ exits the grid on the right.
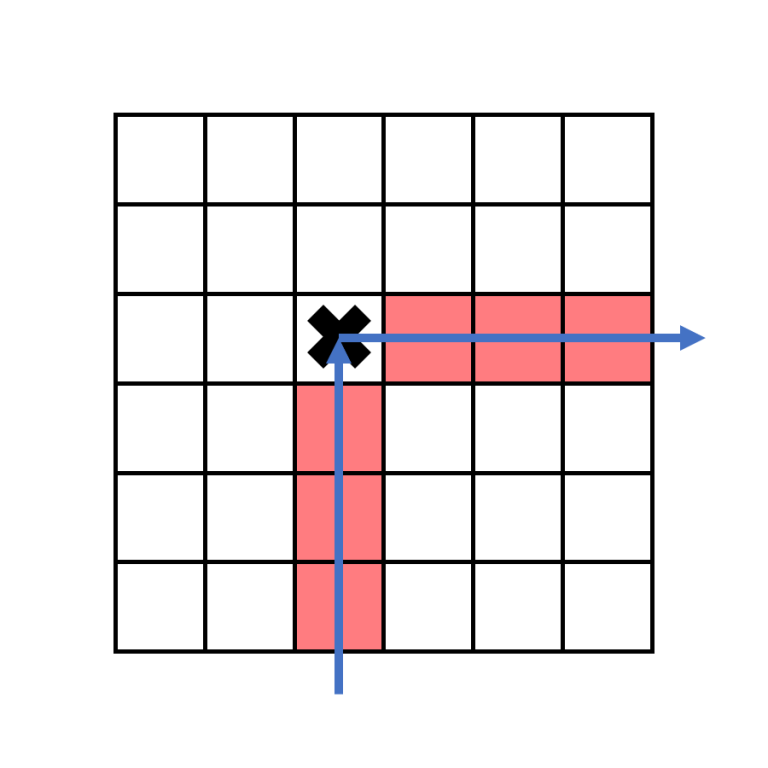
This means that if the target that it hits in on row $$$r$$$, there is no other target to its right on row $$$r$$$.
For columns with $$$a_j=2$$$, the boomerang in column $$$j$$$ has to hit second target in some column $$$k$$$ before moving downwards.
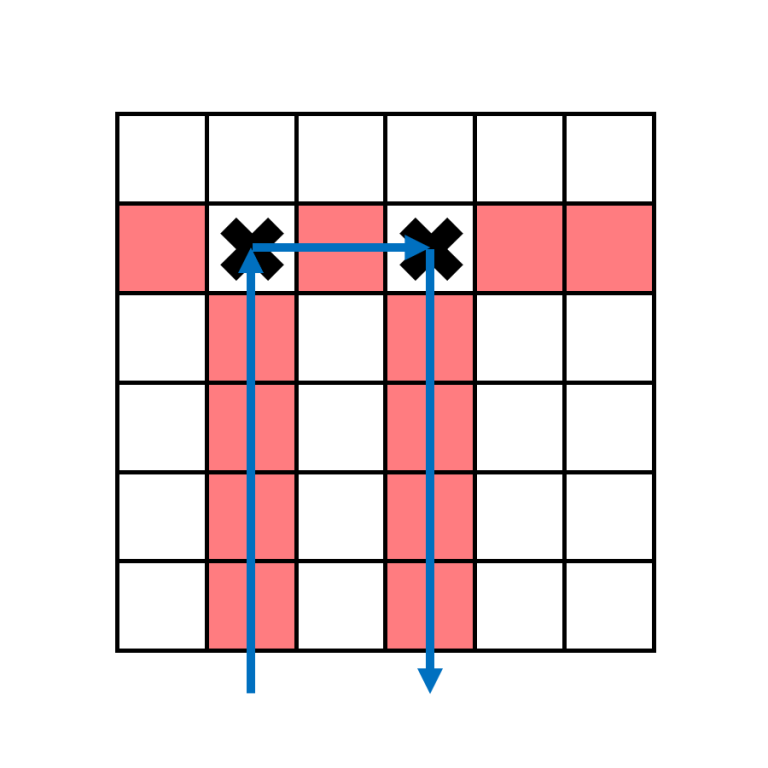
The $$$2$$$ targets that this boomerang hits must be in the same row, and since no row contains more than $$$2$$$ targets, these are the only $$$2$$$ targets in the row. Additionally, there isn't any target below the second target. This means $$$a_k=1$$$.
This tells us that columns $$$j$$$ with $$$a_j=2$$$ must be matched with columns $$$k$$$ with $$$a_k=1$$$ to its right with $$$j < k$$$. If we only had $$$a_j=1$$$ and $$$a_j=2$$$, we can simply greedily match $$$2$$$ s to $$$1$$$ s that are available.
$$$3$$$ s initially seem difficult to handle. The key observation is that $$$3$$$ s can "link" to $$$3$$$ s to its right. The way to do this for the have the first target for one boomerang be the third target for another boomerang.
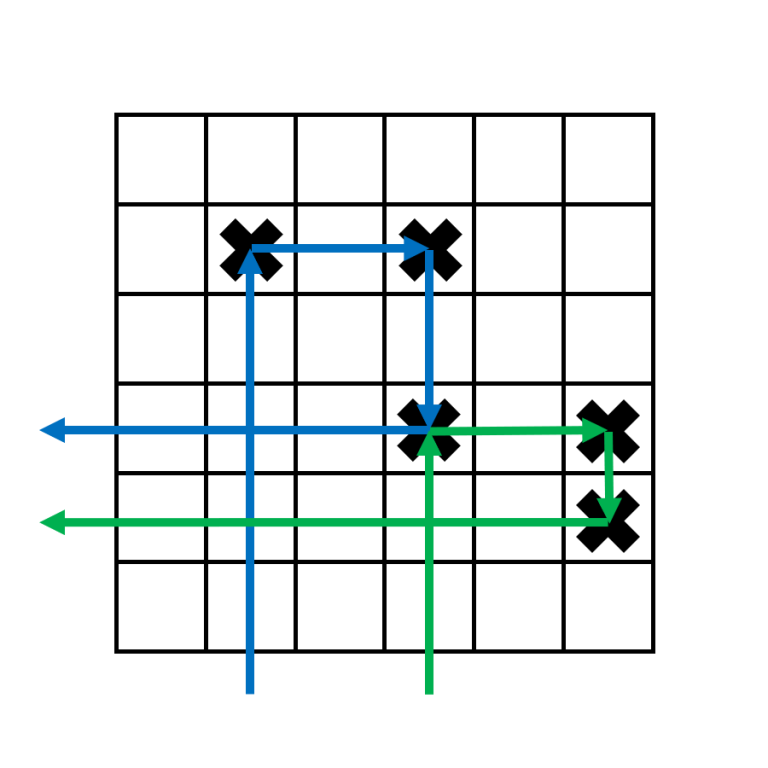
This allows us to "chain" the $$$3$$$ s together in one long chain.
Thus, we only care about the first $$$3$$$, which has to use either a $$$2$$$ or a $$$1$$$ (if it uses a $$$1$$$, that $$$1$$$ cannot be matched with a $$$2$$$). We should always use a $$$2$$$ if possible since it will never be used by anything else, and the exact $$$1$$$ that we use also doesn't matter.
Thus the solution is as follows: Process from right to left. If the current value is a $$$1$$$, add it to a list of available ones. If the current value is a $$$2$$$, match it with an available $$$1$$$ and remove the $$$1$$$ from the list. If the current value is a $$$3$$$, match it with $$$3$$$,$$$2$$$ or $$$1$$$ in that order of preference.
Once we have found the chains and matches, we can go from left to right and give each chain / match some number of rows to use so that they do not overlap. The final time complexity is $$$O(n)$$$.
Bonus $$$1$$$: Show that the directly simulating the path of each boomerang is overall $$$O(n)$$$.
Bonus $$$2$$$ (unsolved): Solve for $$$0 \leq a_j \leq 4$$$.
#include <bits/stdc++.h>
using namespace std;
int N, A[100005], T;
vector<pair<int,int> > targets;
vector<int> ones, twos, threes;
int currow = 1, col[100005], twomatch[100005], threematch[100005];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> N;
for (int i = 1; i <= N; ++i){
cin >> A[i];
}
for (int i = N; i >= 1; --i){
if (A[i] == 1){
ones.push_back(i);
}
else if (A[i] == 2){
if (ones.size() == 0){
cout << -1 << '\n';
return 0;
}
else{
twomatch[i] = ones.back();
ones.pop_back();
}
twos.push_back(i);
}
else if (A[i] == 3){
if (threes.size() > 0){
threematch[i] = threes.back();
}
else if (twos.size() > 0){
threematch[i] = twos.back();
}
else if (ones.size() > 0){
threematch[i] = ones.back();
ones.pop_back();
}
else{
cout << -1 << '\n';
return 0;
}
threes.push_back(i);
}
}
for (int i = 1; i <= N; ++i){
if (col[i] == 1 || A[i] == 0) continue;
int curcol = i;
while (curcol != 0){
col[curcol] = 1;
if (A[curcol] == 1){
targets.emplace_back(currow,curcol);
curcol = 0;
currow++;
}
else if (A[curcol] == 2){
targets.emplace_back(currow,curcol);
curcol = twomatch[curcol];
}
else if (A[curcol] == 3){
targets.emplace_back(currow,curcol);
curcol = threematch[curcol];
targets.emplace_back(currow,curcol);
currow++;
}
}
}
cout << targets.size() << '\n';
for (auto it : targets){
cout << it.first << ' ' << it.second << '\n';
}
}
def die():
print(-1)
exit(0)
ones = []
ans = []
H = 1
lastThree = (-1,-1)
n = int(input())
arr = list(map(int,input().split(" ")))
for i in range(n-1, -1, -1):
if arr[i] == 0:
continue
elif arr[i] == 1:
ones.append((i,H))
ans.append((i,H))
H += 1
elif arr[i] == 2:
if len(ones) == 0:
die()
T = ones[-1]
ones.pop()
ans.append((i, T[1]))
lastThree = (i,T[1])
elif arr[i] == 3:
if lastThree[0] == -1:
if len(ones) == 0:
die()
else:
lastThree = ones[-1]
ones.pop()
ans.append((i, H))
ans.append((lastThree[0], H))
lastThree = (i,H)
H += 1
print(len(ans))
for ii in ans:
print(n-ii[1] + 1, end = ' ')
print(ii[0] + 1)
1428E - Carrots for Rabbits
Setter: errorgorn
Prepared by: errorgorn
Orz proof by: oolimry
Greedy.
Let us define $$$f(l,p)$$$ as the sum of time needed when we have a single carrot of length $$$l$$$ and it is split into $$$p$$$ pieces.
We can show that $$$f(l,p−1)−f(l,p)≥f(l,p)−f(l,p+1)$$$.
Let us define $$$f(l,p)$$$ as the sum of time needed when we have a single carrot of length $$$l$$$ and it is split into $$$p$$$ pieces.
In an optimal cutting for a single carrot, we will only cut it into pieces of length $$$w$$$ and $$$w+1$$$, for some $$$w$$$.
Such cutting is optimal as suppose we have $$$2$$$ pieces of length $$$\alpha$$$ and $$$\beta$$$, and $$$\alpha+2 \leq \beta$$$. Then, it is better to replace those $$$2$$$ pieces of carrots with length $$$\alpha+1$$$ and $$$\beta-1$$$, since $$$(\alpha+1)^2+(\beta-1)^2 \leq \alpha^2+\beta^2$$$.
To calculate $$$f(l,p)$$$, we need to find $$$p_1,p_2$$$ such that $$$p_1 (w) + p_2 (w+1)=l$$$ and $$$p_1+p_2=p$$$, minimizing $$$p_1(w)^2+p_2(w+1)^2$$$.
Clearly, $$$w=\lfloor \frac{l}{p} \rfloor$$$ and $$$p_2=l\mod p$$$. Thus, calculating $$$f(l,p)$$$ can be done in $$$O(1)$$$.
We can use the following greedy algorithm. We consider making zero cuts at first. We will make $$$k$$$ cuts one by one. When deciding where to make each cut, consider for all the carrots, which carrot gives us the largest decrease in cost when we add an extra cut. If a carrot of length $$$l$$$ currently is in $$$p$$$ pieces, then the decrease in cost by making one extra cut is $$$f(l,p) - f(l,p+1)$$$.
The important observation here is that $$$f(l,p-1)-f(l,p) \geq f(l,p)-f(l,p+1)$$$.
Consider $$$f(2l,2p)$$$.
Since the length is even and we have an even number of pieces, we know that the will be one cut down the middle and each half will have $$$p$$$ pieces. As such, $$$f(2l,2p) = 2f(l,p)$$$ This is because there even number of $$$w$$$ length pieces and an even number of $$$w+1$$$ length pieces, hence the left half and the right half are the same.
Also, $$$f(l,p-1) + f(l,p+1) \geq f(2l,2p)$$$, since $$$f(l,p-1) + f(l,p+1)$$$ is describing cutting a carrot of length $$$2l$$$ first into $$$2$$$ carrots of length $$$l$$$ and cutting it into $$$p-1$$$ and $$$p+1$$$ pieces respectively. The inequality must hold because this is a way to cut a carrot of length $$$2l$$$ into $$$2p$$$ pieces.
Since we have $$$f(l,p-1) + f(l,p+1) \geq f(2l,2p)$$$ and $$$f(2l,2p) = 2f(l,p)$$$.
We have $$$f(l,p-1) + f(l,p+1) \geq f(l,p) + f(l,p)$$$.
Rearranging terms gives $$$f(l,p-1)-f(l,p) \geq f(l,p)-f(l,p+1)$$$
In other words, the more cuts we make to a carrot, there is a diminishing returns in the decrease in cost per cut. As such, For any carrot, we don't need to think about making the $$$(p+1)$$$-th cut before making the $$$p$$$-th cut.
Hence, all we need to do is choose carrot with the largest decrease in cost, and add one extra cut for that. Which carrot has the largest decrease in cost can be maintained with a priority queue. Hence, we get a time complexity of $$$O(klog(n))$$$.
Bonus: solve this problem for $$$k \leq 10^{18}$$$.
When preparing this problem, I started with putting $$$n,k\leq 5000$$$ because i thought if I put larger values it would be guessforces. However, several testers made $$$O(nk \log n)$$$ and $$$O(nk)$$$ dp solutions. Which version of the problem do you think is better?
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ll,ii>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl;
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n,k;
ll cost=0;
priority_queue<iii> pq;
ll sq(ll i){
return i*i;
}
ll val(ll len,ll nums){
ll unit=len/nums;
ll extra=len-unit*nums;
return (nums-extra)*sq(unit)+extra*sq(unit+1);
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
rep(x,0,n){
ll t;
cin>>t;
cost+=sq(t);
pq.push(iii(val(t,1)-val(t,2),ii(t,2)));
}
rep(x,0,k-n){
cost-=pq.top().fi;
int a=pq.top().se.fi,b=pq.top().se.se;
pq.pop();
pq.push(iii(val(a,b)-val(a,b+1),ii(a,b+1)));
}
cout<<cost<<endl;
}
from heapq import *
n,k=map(int,input().split(" "))
def val(l,nums):
unit=l//nums
extra=l-unit*nums
return (nums-extra)*unit*unit+extra*(unit+1)*(unit+1)
pq=[]
arr=list(map(int,input().split(" ")))
total=0
for x in range(n):
total+=arr[x]*arr[x]
heappush(pq,(-val(arr[x],1)+val(arr[x],2),arr[x],2))
for x in range(k-n):
temp=heappop(pq)
total+=temp[0]
a,b=temp[1],temp[2]
heappush(pq,(-val(a,b)+val(a,b+1),a,b+1))
print(total)
1428F - Fruit Sequences
Setter: bensonlzl
Prepared by: dvdg6566
Line sweep.
How does $$$f(l,r)$$$ change when we increase r?
For a fixed $$$r$$$, let us graph $$$f(l,r)$$$ in a histogram with $$$l$$$ as the $$$x$$$-axis. We notice that this histogram is non-increasing from left to right. Shown below is the histogram for the string $$$11101011$$$ with $$$r = 6$$$, where $$$1$$$ box represents $$$1$$$ unit.
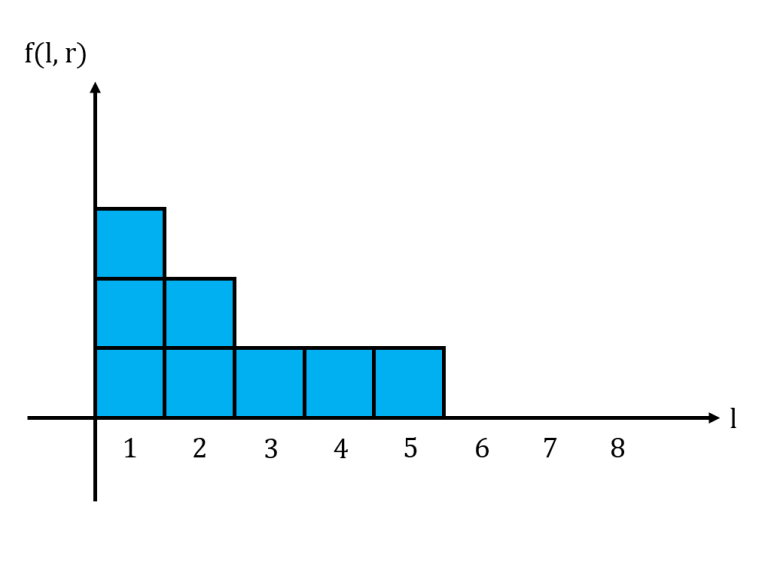
The area under this histogram is the sum of all $$$f(l,r)$$$ for a fixed $$$r$$$. Consider what happens to the histogram when we move from $$$r$$$ to $$$r+1$$$. If $$$s_{r+1} = 0$$$, then the histogram does not change at all. If $$$s_{r+1} = 1$$$, then we may need to update the histogram accordingly.
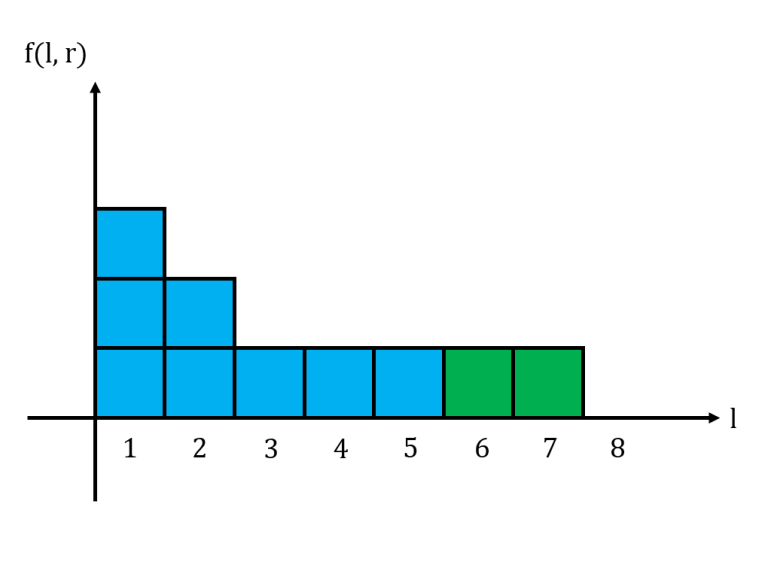
Above is the histogram for $$$11101011$$$ when $$$r=7$$$.
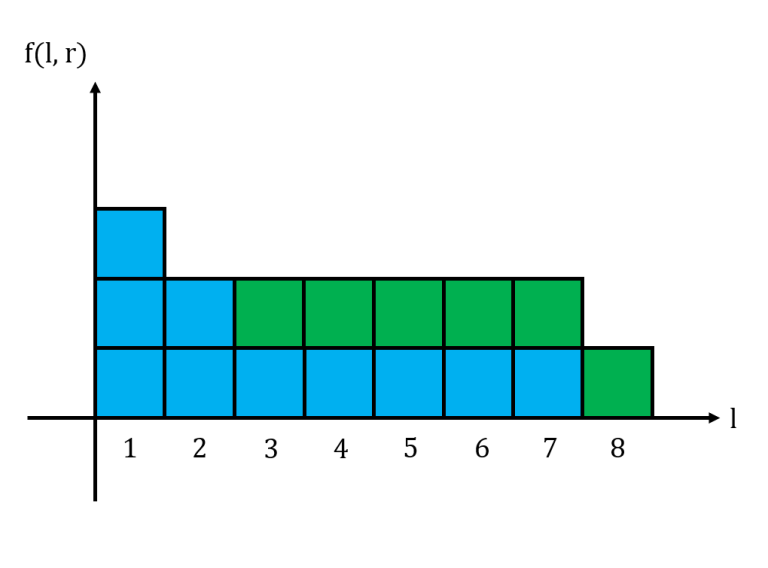
And this is the histogram for $$$11101011$$$ when $$$r=8$$$.
When adding a new segment of $$$k$$$ $$$1$$$s, we essentially fill up the bottom $$$k$$$ rows of the histogram. Thus, we let $$$L_x$$$ be the largest $$$l$$$ such that $$$f(l,r) = x$$$. We maintain these $$$L_x$$$ values in an array. When we process a group of $$$k$$$ 1s, we update the values for $$$L_1, L_2, \cdots, L_k$$$, change the area of the histogram and update the cumulative sum accordingly.
With proper processing of the segments of 1s, this can be done in $$$O(n)$$$ time.
Interestingly, many testers found F not much harder than E, as such we gave them the same score. However, it seems that F was signficicantly harder than E based on the number of solves. Another thing was that FST for this problem were caused by testdata that involved sequences of '1's of increasing length.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll hist[2000005], tot = 0, cur = 0;
int N, S[2000005];
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
cin >> N;
for (int i = 1; i <= N; ++i){
char x;
cin >> x;
S[i] = (x - '0');
}
for (int i = 1; i <= N; ++i){
if (S[i] == 0) tot += cur;
else{
int l = i, r = i;
while (r < N && S[r+1] == 1) r++;
for (int x = 1; x <= (r-l+1); ++x){
cur += (l-1+x) - hist[x];
tot += cur;
hist[x] = r-x+1;
}
i = r;
}
}
cout << tot << '\n';
}
import sys
range = xrange
input = raw_input
inp=sys.stdin.read().split()
n = int(inp[0])
s=inp[1]
tot=0
cur=0
hist=[0]*1000005
i=0
while (i<n):
if (s[i]=='0'):
tot+=cur
else:
l=i
r=i
while (r+1<n and s[r+1]=='1'): r+=1
for x in range(r-l+1):
cur+=(l+x+1)-hist[x]
tot+=cur
hist[x]=r-x+1
i=r
i+=1
print(tot)
1428G1 - Lucky Numbers (Easy Version), 1428G2 - Lucky Numbers (Hard Version)
Setter: oolimry
Prepared by: oolimry
0 is a lucky number as well.
There is at most one number whose digits is not entirely 0, 3, 6, 9.
Knapsack.
Group same items.
Suppose in our final solution, there is a certain position (ones, tens...) that has two digits which are not $$$0$$$, $$$3$$$, $$$6$$$, or $$$9$$$. Let these two digits are $$$a$$$ and $$$b$$$. If $$$a+b \leq 9$$$, we can replace these two digits with $$$0$$$, and $$$a+b$$$. Otherwise, we can replace these two digits with $$$9$$$ and $$$a+b-9$$$. By doing this, our solution is still valid as the sum remains the same, and the total fortune will not decrease since $$$a$$$ and $$$b$$$ are not $$$3$$$, $$$6$$$ or $$$9$$$.
As such, in the optimal solution, there should be at most one number that consists of digits that are not $$$0$$$, $$$3$$$, $$$6$$$ or $$$9$$$. Let's call this number that has other digits $$$x$$$.
Easy Version
Since there's only one query, we can try all possibilities of $$$x$$$. The question reduces to finding the maximum sum of fortune among $$$k-1$$$ numbers containing the digits $$$0$$$, $$$3$$$, $$$6$$$ and $$$9$$$ that sum up to exactly $$$n-r$$$. We can model this as a 0-1 knapsack problem, where the knapsack capacity is $$$n-r$$$.
For the ones position, the value (fortune) can be increased by $$$F_0$$$ for a weight of $$$3$$$ a total of $$$3(k-1)$$$ times, so we can create $$$3(k - 1)$$$ objects of weight $$$3$$$ and value $$$F_0$$$. For tens it's $$$F_1$$$ for a weight of $$$30$$$, and so on. Since there are many duplicate objects, we can group these duplicate objects in powers of $$$2$$$. For example, $$$25$$$ objects can be grouped into groups of $$$1$$$, $$$2$$$, $$$4$$$, $$$8$$$, $$$10$$$.
This runs in $$$O(ndlogk)$$$ where $$$d$$$ is the number of digits (6 in this case)
Hard Version
In the hard version, we are not able to search all $$$n$$$ possibilities for the last number $$$x$$$ as there are many queries.
Using the 0-1 knapsack with duplicates, we have computed the dp table for the first $$$k-1$$$ numbers. The rest is incorporating the last number into the dp table. We can do this by considering each digit separately. Then, we can update the dp table by considering all possible transitions for all digits from $$$0$$$ to $$$9$$$.
#include <bits/stdc++.h>
using namespace std;
static long long inf = (1LL << 58LL);
static long long F[6];
static long long ten[6] = {1, 10, 100, 1000, 10000, 100000};
static long long dp[1000005];
int N, K;
int main(){
cin >> K;
for(int i = 0;i <= 5;i++) cin >> F[i];
int Q; cin >> Q;
assert(Q == 1);
int N; cin >> N;
///0-1 knapsack with duplicate elements
fill(dp,dp+N+1,-inf); dp[0] = 0;
for(int d = 0;d <= 5;d++){
long long left = 3 * (K - 1);
long long group = 1;
///grouping 3*(K-1) elements into groups of powers of 2
while(left > 0){
group = min(group, left);
long long value = group * F[d];
long long weight = group * ten[d] * 3;
for(int i = N;i >= weight;i--) dp[i] = max(dp[i], dp[i-weight] + value); ///knapsack DP
left -= group;
group *= 2;
}
}
long long ans = 0;
for(int X = 0;X <= N;X++){
///calculating the fortune of X
long long fortune = 0;
int x = X;
for(int d = 0;d <= 5;d++){
int rem = x % 10;
if(rem == 3 || rem == 6 || rem == 9) fortune += (rem / 3) * F[d];
x /= 10;
}
ans = max(ans, fortune + dp[N-X]);
}
cout << ans;
}
#include <bits/stdc++.h>
using namespace std;
const long long inf = (1LL << 58LL);
long long F[6];
long long fortune[10] = {0, 0, 0, 1, 0, 0, 2, 0, 0, 3};
long long ten[6] = {1, 10, 100, 1000, 10000, 100000};
long long dp[1000005];
int main(){
ios_base::sync_with_stdio(false); cin.tie(0);
int K; int N = 999999;
cin >> K;
for(int i = 0;i <= 5;i++) cin >> F[i];
fill(dp,dp+N+1,-inf); dp[0] = 0;
for(int d = 0;d <= 5;d++){
long long left = 3 * (K - 1);
long long group = 1;
///grouping 3*(K-1) elements into groups of powers of 2
while(left > 0){
group = min(group, left);
long long value = group * F[d];
long long weight = group * ten[d] * 3;
for(int i = N;i >= weight;i--) dp[i] = max(dp[i], dp[i-weight] + value); ///knapsack DP
left -= group;
group *= 2;
}
}
for(int d = 0;d <= 5;d++){
for(int i = N;i >= 0;i--){
for(int b = 1;b <= 9;b++){
int pre = i - ten[d] * b;
if(pre < 0) break;
dp[i] = max(dp[i], dp[pre] + fortune[b] * F[d]);
}
}
}
int Q; cin >> Q;
while(Q--){
int n; cin >> n;
cout << dp[n] << "\n";
}
}
1428H - Rotary Laser Lock
Setter: bensonlzl and oolimry
Prepared by: bensonlzl
Using only arc $$$0$$$, find at least $$$1$$$ position where arc $$$0$$$ exactly matches another arc.
Binary Search.
Algorithm Analysis
Flatten the circle such that it becomes $$$n$$$ rows of length $$$nm$$$ with vertical sections numbered from $$$0$$$ to $$$nm-1$$$ that loops on the end. We say that the position of an arc is $$$x$$$ if the left endpoint of the arc is at section $$$x$$$. Indices are taken modulo $$$nm$$$ at all times. Moving arcs right is equivalent to rotating them clockwise, and moving arcs left is equivalent to rotating them counter-clockwise.
Notice that if we shift arc 0 right and the display increases, then the leftmost section of arc 0 had no other arcs in the same section. Thus, if we shift arc 0 right again and the display does not increase, we are certain that there was another arc at that position, so we shift arc 0 left. We now enter the detection stage to find any arc that coincides with arc 0 (of which there exists at least 1) at this position. Let's note down this positions as $$$x$$$.
Let $$$S$$$ be the set of arcs that we do not know the positions of yet (this set initially contains all arcs from 1 to $$$N-1$$$) and $$$T$$$ and $$$F$$$ be an empty sets. $$$T$$$ will be the set of all candidate arcs (those that may coincide here) and $$$F$$$ will contain all arcs that we have shifted leftwards. Take all elements in $$$S$$$ and put them in $$$T$$$, and pick half of the elements in $$$S$$$ and add them to the set $$$F$$$. We now shift all elements in $$$F$$$ left.
We move arc 0 left to check if any arc is at position $$$x-1$$$.
If there is, then we know that an arc that initially coincided at $$$x$$$ lies in $$$F$$$. In this case, we set $$$T$$$ to $$$T \cap F$$$ (elements of $$$T$$$ that are in $$$F$$$), pick half of the elements in $$$T$$$ to move right and remove those from $$$F$$$.
If no arc is at position $$$x-1$$$, then the arc we are looking for lies in $$$T \ \backslash \ F$$$ (elements in $$$T$$$ that are not in $$$F$$$). We set $$$T$$$ to be $$$T \ \backslash \ F$$$ and pick half of $$$T$$$ to move left and add those to $$$F$$$. We then shift arc 0 right and recurse.
When we have narrowed $$$T$$$ to exactly 1 arc, we know where exactly that arc is now. We shift that arc left such that its right endpoint is at $$$x-2$$$ so that it does not cover position $$$x-1$$$, which we may still need for future tests. Now we remove the arc found from $$$S$$$ and leave the detection stage and continue searching for the other arcs.
Once we have found all $$$n-1$$$ other arcs, we find the relative position to arc 0 and print them as the final output.
Query Analysis
Whenever we shift arc 0 right and are not in the detection stage, we use 1 shift. This occurs at most $$$2nm-m$$$ times because it takes up to $$$nm-m$$$ shifts right to find the first position where arc 0 coincides, and another $$$nm$$$ to traverse the entire circle again to find all of the arcs.
Whenever we enter the detection stage, we find one arc and use $$$2$$$ shifts initially when we move arc 0 right then left, yielding a total of $$$2n-2$$$ such shifts. Each binary search requires $$$2 \log |T|$$$ shifts of arc 0 (left and right), so across the $$$n-1$$$ detection stages this is at most $$$2n\log n$$$ when summed across all stages.
The way we perform the binary search is quite important here. Performing it in a naive manner (e.g. shifting half left, test and shifting them back) can use up to $$$n^2$$$ queries.
Instead, we set the number of elements that move in / out of $$$F$$$ at each iteration of the binary search to be the smaller half. This way we can guarantee that the number of shifts done by the candidate arcs is at most the total number of candidate arcs in the first place. This becomes $$$\frac{n(n-1)}{2}$$$ since we start with $$$n-1$$$ candidate arcs and reduce that number by 1 after each detection stage.
When we shift each of the arcs left by $$$m$$$ or $$$m+1$$$ (depending on whether they were in $$$F$$$ when we narrowed it down to 1 arc), we use at most $$$(n-1)(m+1) = nm+n-m-1$$$ shifts.
Thus in total, we use at most $$$2nm-m+2n-2+2n\log n + \frac{n(n-1)}{2} + nm+n-m-1$$$ shifts. For $$$n=100,m=20$$$, this is less than $$$13000$$$, which is much lower than the query limit of $$$15000$$$.
Other Comments
The limit was set higher than the provable bound to allow for other possible solutions. At least $$$1$$$ tester found a different solution that used around $$$13500$$$ queries.
Some other optimizations that empirically improve the number of queries:
Instead of using arc $$$0$$$ as the detector, we can randomly pick one of the $$$n$$$ arcs as the detector arcs.
At the very beginning, we perform some constant number of random shifts of the arcs (e.g. $$$300$$$ to $$$400$$$ random shifts). This helps to break up long groups of arcs that overlap, which speeds up the initial $$$nm$$$ search.
The official solution, augmented with these optimizations uses well below $$$11500$$$ queries and is very consistent for non-handcrafted test cases.
#include <bits/stdc++.h>
using namespace std;
int queryRotation(int r, int d){ // Auxiliary function to print query and receive answer
int res;
cout << "? " << r << ' ' << d << endl << flush; // Print query
cout.flush();
cin >> res; // Get response
if (res == -1) exit(1); // Error occured, exit immediately
else return res; // Return result
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0);
int N, M; // Number of rings and number of sections per ring
int totalPositions; // totalPositions = N*M
int newNum;
int currentNum; // track the current number on the display (responses from interactor)
int state = 0; // 0 means searching for rings, 1 means finding the ring at this position
int relpos[105] = {}; // Array to store the final relative positions
cin >> N >> M;
totalPositions = N*M;
// While this statement doesn't do anything,
// it serves as a reminder that we are taking
// the initial starting position of ring 0
// to be position 0
relpos[0] = 0;
currentNum = queryRotation(0,1);
relpos[0] = (relpos[0] + 1) % totalPositions;
// Now we prepare the set of unknown rings S
vector<int> S;
for (int i = 1; i < N; ++i){
S.push_back(i);
}
// We now perform a preliminary rotation of ring 0 around until
// we are certain that ring 0 coincides with another ring
// at its leftmost point and the section to its left is empty
// This occurs when the difference changes from increasing when
// ring 0 moves right to non-increasing when ring 0
// moves right
int hasIncreased = 0;
while (1){
// Rotate once, get the new number
newNum = queryRotation(0,1);
relpos[0] = (relpos[0] + 1) % totalPositions;
// Check if the number has increased
if (newNum > currentNum){
hasIncreased = 1;
currentNum = newNum;
}
else{ // Otherwise the number hasn't increased
currentNum = newNum;
// Check if we have increased before
if (hasIncreased){
// If we have, it means that our previous position
// coincided with the left endpoint of another arc
// Time to begin the detection stage
state = 1;
currentNum = queryRotation(0,-1);
relpos[0] = (relpos[0] - 1 + totalPositions) % totalPositions;
break;
}
}
}
while (!S.empty()){ // While we haven't found all of the rings yet
if (state == 1){ // If we are searching for an arc here
int curArc = 0; // to store the new arc
vector<int> T = S; // set of candiate arcs
vector<int> F; // set of arcs that have been moved left
for (int i = 0; i < T.size()/2; ++i){ // take the smaller half
F.push_back(T[i]);
currentNum = queryRotation(T[i],-1);
}
while (T.size() > 1){ // while the number of candidate arcs is > 1, we binary search on the remaining arcs
int newNum = queryRotation(0,-1);
relpos[0] = (relpos[0] - 1 + totalPositions) % totalPositions;
if (newNum >= currentNum){ // the arc that we are looking for lies in F
// Set T to F
T.clear();
for (auto it : F){
T.push_back(it);
}
// Half the size of F by moving the smaller half to the right
int sz = F.size()/2;
for (int i = 0; i < sz; ++i){
int revRing = F.back();
currentNum = queryRotation(revRing,1);
F.pop_back();
}
}
else{ // the arc we are looking for does not lie in F
vector<int> temp;
for (auto it1 : T){
int check = 0;
for (auto it2 : F){
if (it1 == it2) check = 1;
}
if (!check) temp.push_back(it1);
}
T = temp;
F.clear();
for (int i = 0; i < T.size()/2; ++i){ // take the smaller half once again
currentNum = queryRotation(T[i],-1);
F.push_back(T[i]);
}
}
currentNum = queryRotation(0,1); // bring arc 0 back
relpos[0] = (relpos[0] + 1) % totalPositions;
}
curArc = T[0]; // we have found the arc
// we want this arc to be M+1 sections away from the current position
// of arc 0 so that it does not interfere with later searches
if (!F.empty()){ // the arc we found still lies in F
for (int i = 0; i < M; ++i){ // move the arc back by M sections
currentNum = queryRotation(curArc,-1);
}
relpos[curArc] = relpos[0] - M - 1;
}
else{ // the arc we found does not lie in F
for (int i = 0; i <= M; ++i){ // move the arc back by M+1 sections
currentNum = queryRotation(curArc,-1);
}
relpos[curArc] = relpos[0] - M - 1;
}
// We now remove curArc from S
vector<int> temp;
for (auto it : S){
if (it != curArc) temp.push_back(it);
}
S.clear();
for (auto it : temp) S.push_back(it);
state = 0;
currentNum = queryRotation(0,-1);
relpos[0] = (relpos[0] - 1 + totalPositions) % totalPositions;
hasIncreased = 0;
}
else{ // keep moving right
newNum = queryRotation(0,1);
relpos[0] = (relpos[0] + 1) % totalPositions;
if (newNum <= currentNum && hasIncreased == 1){ // start searching
newNum = queryRotation(0,-1);
relpos[0] = (relpos[0] - 1 + totalPositions) % totalPositions;
state = 1;
}
else if (newNum > currentNum) hasIncreased = 1;
currentNum = newNum;
}
}
cout << "! ";
for (int i = 1; i < N; ++i){
cout << (((relpos[i] - relpos[0] + 5 * totalPositions)%totalPositions) + totalPositions) % totalPositions << ' ';
}
cout << endl << flush;
}










Auto comment: topic has been updated by oolimry (previous revision, new revision, compare).
Is this posted before 5 hours, or is there a way to post only for private?
of course
It was drafted 5 hours ago, but most likely posted a few minutes ago.
it's something like a draft. the draft was created about 5 hours ago, but never got posted until just now
Fast editorial.
I love the approach of adding hints in editorial.It really helps a lot by solving problem without seeing exact solution. Nice editorial!
Giving some hints before showing the exact solution is very helpful(as it helps to think better). How nice it would be if everyone wrote the editorials like this!
It would be very helpful if this style of adding hints is made mandatory.
fast editorial
So Fast!!!
Loved the problem statements!!!
having lots of templates in the editorial codes makes the code harder to undrastand. if the codes were with less template(or the template which almost every one have like ll) it would be better.
Any ideas for solving E for k<=1e18?
monge, aka Lagrange speedup or aliens trick
It seems it's too slow unless you can get rid of second bsearch: link. (Not to mention overflow for higher values)
Edit: Using cuom1999's optimization below, I also ended up getting AC: link.
I was able to get AC with some very similar code (95816754), but one second does seem to be a somewhat tight time limit, at least for these approaches.
May i ask a question? why i submit your AC code, but it show TLE on Test6
oh, i change the lang to G++17(64), it ac now, do you konw the reason?
We can estimate the second binary search like this.
Let's denote $$$cost(a, b)$$$ cost of dividing $$$a$$$ carrots to $$$b$$$ rabbits. We want to find $$$b$$$ such that $$$cost(a, b) + C * b$$$ is minimized, where $$$C$$$ is the parameter in Alien Trick.
We can estimate $$$cost(a, b)=b*(\dfrac{a}{b})^2=a^2/b$$$. So $$$cost(a, b) + C * b = \dfrac{a^2}{b} + Cb$$$.
This is minimized when $$$b$$$ is around $$$\dfrac{a}{\sqrt{C}}$$$. We can binary search only $$$50-100$$$ values around this number. Link 95819034
P/S: This analysis gives us the hint that $$$C$$$ should be around $$$O(max(a_i)^2)$$$ in the worst case, which means we should binary search $$$C$$$ from $$$0$$$ to $$$~10^{12}$$$. I got WA due to ignoring this :(.
Maybe WQS
that's called "Alien trick" in other countries (WQS binary search in China)
the word Alien is referring to IOI2016 D2T3
I think that it's more often called "parametric search" or "lambda optimization".
More often called Lagrange multipliers.
Hey, where can I learn this trick/search technique? Is there a particular resource that helped you? I have tried out a few resources (hard to follow sometimes because of language differences), the intuition is clear but the proofs of convexity are generally missing. Any links that have a rigorous explanation of this trick?
Suppose $$$n < k$$$ and consider the priority queue solution described in the editorial. The last cut added will have some value $$$V$$$. The idea is that there will be at least $$$k - n$$$ cuts possible to make with value at least $$$V$$$, but fewer than $$$k - n$$$ cuts possible to make with value greater than $$$V$$$, and this number of cuts can be calculated in $$$O(n \log(\max a_i))$$$, also using binary search. After finding $$$V$$$ the answer is easy enough to calculate: Make every possible cut with value at least $$$V$$$. Calculate the total eating time for this many cuts, then account for any extra cuts made by adding $$$V \cdot ((\text{cuts actually made}) - (k - n))$$$, since every extra cut has value exactly $$$V$$$.
The overall time complexity of this is $$$O(n (\log (\max a_i))^2)$$$.
How come everybody suddenly started hacking 'B'?
It is addressed in "other comments"
I solved A, B, C and then I tried D and then I tried D and then I tried D.. and then contest was over. ;-;
I'm pretty stuck too :/
I forgot about linking-3-with-3 case in problem D
big F
I hate problem D.
I really like these hints in editorials. Sometimes I feel its better to see hints and work through them instead of seeing full editorial. Thank you so much.
.
The answer will not be worse if there is at most one number whose digits is not entirely 0, 3, 6, 9. ans = [ 96, 94 ]
yup got it few second after I commented
Thanks ^^
G: 0/K knapsack can be solved in same time complexity with 0/1 knaspack using deque, improving time complexity of the knapsack part to $$$O(nd)$$$.
I actually did not know that, thanks for sharing! I was confused at first by the large number of solutions which used deque.
What is wrong with normal Priority queue implementation in E?
priority_queue<int,vector> pp; for(int i = 0; i<n; i++){ pp.push(a); }
while(pp.size() < k){ int x = pp.top(); pp.pop(); pp.push(x/2); pp.push((x+1)/2); } int sum = 0; while(!pp.empty()){ sum += pp.top()*pp.top(); pp.pop(); } cout << sum ;
10, 3 is split into 3,3,4. Your implementation changes to 2,3,5
Fast Editorial and the Editorial is really nice. Thanks to the setters and testers.
Am i the only one that overkilled B with SCC?
overkilling is an understatement.
Almost everyone in rank $$$1 \sim 20$$$: HACK PROBLEM B!!!
Me: see that? GO HACK PROBLEM B!!!
checked every code in my room...
my room:
This time I am unluck either :( When can I arrive LGM again QwQ
Congratulations on achieving LGM!!!
Today! :)
Congratulations! LGM Dreamoon!
Can anyone please tell me what is that why that green red color appears when I open any solution in my room? One more question- If I open a solution and don't hack it, will I get any penalty for that?
As a new comer, i really enjoyed this contest and found the contest interesting .Thanks a lot !!
Why is there a preference of choice for matching 3 in D??? Update: Got it!!!
I think this is to save maximum 1's for the columns having 2's in the left. Because 2's can only be matched to the unmatched 1's in the right.
Thanks for adding hints, fast editorial and nice problems.D was beautiful
I really appreciate the hints in this editorial, they give a different perspective to problem upsolving. I hope to go up in rating after a long time!
your contribution is a positive .... for now ....
[Deleted]
For this case, you would split the carrot into 2, 3, 5 but the optimal solution is 3, 3, 4.
[Deleted]
[Deleted]
For problem C:
Bonus: what is the length of the longest string that Zookeeper can make such that there are no moves left?
Would running the same algorithm on the reversed string be a correct approach?
reason for that might be if we iterate from right to left if we encounter 'A' and we push it on top of stack and now if we move left further now on matter if we encounter a 'A' or a 'B' that would result in a string 'AA' or 'BA' (?A) and we can't delete either of them
BUT
if we go from left to right and we encounter 'A' we push it on top of stack than if their exist at least 1 'B' on going right we pop from stack that 'A'
An alternative solution for F: This problem can be solved by using Segment Tree Beats, specifically one of type 2. If we consider a sweep from left to right, storing the maximum segment from 1 to i in a subarray, we can clearly see that the maximum in the current run increases by one, otherwise you can take the maximum of the previous value and the current run. Complexity O(n log^2 n), which actually ACs with a lot of time to spare. I don't really know why. Code: 95789626.
P.S. The main advantage of this solution is that it uses zero brainpower and that you can copy STB templates online.
yes. i actually solved F in about 5 minutes because of this. we tried to kill segment tree beats but other setters wanted nlogn segment tree to pass comfortably. i think that some segment tree beats solutions got killed by our anti segment tree beats testcases tho.
For E, why is it not possible to consider all the carrots in 1 large carrot? Thank you https://codeforces.com/contest/1428/submission/95799505
You cannot glue carrot pieces together, so for example if you had a length 10 and a length 2 the optimal cut is 5, 5, 2.
Idk why some people hating D, but I found it pretty nice. Here is my solution:
Let's process columns from left to right, consider column $$$i$$$ with value $$$2$$$, as explained in editorial we need to connect it with some column $$$j$$$ on the right of it with value $$$1$$$. In order to do that we can just put target to cells $$$(i, i)$$$ and $$$(i, j)$$$. Also, we should skip column $$$j$$$ in later iterations.
For columns with value $$$3$$$ we can connect them with any column with non-zero value and in the same way we add targets to cells $$$(i, i)$$$ and $$$(i, j)$$$. (Note that 3rd part of chain will be added automatically to the cell $$$(j, j)$$$ when we process column $$$j$$$).
And finally for columns with value $$$1$$$, we can just put target to cell $$$(i,i)$$$. It's always safe because there are enough rows for each column
lol as a setter, D gives me trauma from super trees (IOI)
F can also be solved with divide and conquer in O(nlogn).
Let g(l,r) be the answer for a segment. Obviously g(l,r) = g(l,m) + g(m+1,r) + "the rest". If you guarantee s[m]!=s[m+1], then "the rest" can be calculated easily with some prefix/suffix max dp and two pointers.
Here's a solution video (for A-F) that ends up being more about anxiously waiting to see if I got IGM
the way this editorial is formatted and things have been explained ! Kudos for it , I loved the proof in Problem E part
Why has the picture in the 1428B - Belted Rooms changed?
.
My solution for D fails in 11th case. The initial part of the case seems to contain 3 3 3 3 ...
I had tested my code for 3 3 3 ... 1 and 3 3 3 ... 2 1 I think 3 3 3 ... 3 3 should return -1 and so is my code returning.
Where am I going wrong? Thanks. My soln.: https://codeforces.com/contest/1428/submission/95817367
You don't see the whole test, there might be some random numbers, or maybe some 3's at the beginning, then 2's, then 1's. I'll try to find the mistake, but not sure if I can.
Still can't get why greedy solution works for E
how to solve problem D if a[i] >= 4 ?
We will iterate the array from right to left and will maintain two vectors:
One storing the co-ordinates(x,y) with only one target in the xth row
and another storing the co-ordinates(x,y) with two targets in the xth row.
Lets name the vector of first type as "ones" and of second type as "twos" .
We will also keep track of the rows which are empty (will be explained later ) .
We don't have to do anything here
We will have to keep the target in (x1,y1) with x1 being an empty row and y1 = i (Don't fuss about 0-indexing)
For a[i] = 2: we will keep the target in (x,y) where x will be a row with a single element in it (we will get this element from vector "ones") and y = i . we will add this point in vector "twos".
We can choose an element from vector "twos" or vector "ones" but "twos" is to be preferred (work this out yourself or see the editorial) . We have to add two points: one (x1,y1) with x1 being an empty row and y1 = i and another (x1,y2) with y2 equal to the y co-ordinate of the chosen element. We will add (x1,y1) to vector "twos".
Ans : We need an empty row when a[i]= 1 or a[i]=3 .We will use the rows from bottom to top.
In other words : initialize a variable last_empty = n and whenever an empty row is used do last_empty-- .
This concludes it for a[i]<=3.
If you observe the vector "twos" carefully you would see it was storing the point(a,b) with the condition that there is also a point with x coordinate as a and with y co-ordinate as y2>b . For a[i] <= 4 we need to store this second point.
Ans : In a[i] == 2
a[i]=2 : Add the element which was chosen from vector "ones" .
When a[i] = 4 : We will have to add two points : one (x1,y1) with x1 being an empty row and y1 = i and another point(x1,y2) with y2 equal to the y co-ordinate of the chosen element(choose it from the new set of points). we will also add (x1,y1) to vector twos.
I solved it for a[i]<=4.bensonlzl does the solution seem right to you ?
If I'm understanding your solution correctly, your idea is to match a 4 with a 2-1 pair by storing the column of the 1 that the 2 was matched to. This brings up 3 problems (which I also encountered while solving).
The first problem is that it is not obvious what the order of processing should be, because the 2-column can lie between the 4-column and the 1-column or it can be to the left of both the 4-column and the 1-column Consider the 2 testcases :
The second problem is that it is not necessary for the 4 to always match to a 2-1. Consider the following test case:
This is solvable using the following configuration (_ for blank and X for target)
This means that if we process from right to left, we can actually create incomplete 4-1 pairs that are matched to the upper target of columns to their left which do not affect the lower target.
In fact, while working on the $$$a[i] \leq 4$$$ case, I stumbled upon a way to chain 4-columns:
The above configuration gives the sequence $$$1,4,1,4,1,4,1$$$. What I discovered was that chaining $$$4$$$-columns can be very messy because a 4 matched to a 1 at column $$$i$$$ can chain to any other 4 to the left of column $$$i$$$, and thus the 4 chains can end up all over the place.
The third problem is that row configurations come into play here. In the $$$a[i] \leq 3$$$ case, it was relatively easy to deal with the up and down movement of the boomerang. But it gets harder for $$$a[i] \leq 4$$$. An example is the following test case:
This has no solution, because the 4-column needs a 4th target from the 3-column, but that would make it impossible for the boomerang in the 3-column to go down and find any other target.
The point is, if someone can find a solution to $$$a[i] \leq 4$$$, I would be very happy. However, $$$a[i] \leq 4$$$ is when row configurations start to matter and where chains and matchings become very messy, so I gave up on solving this and use $$$a[i] \leq 3$$$.
Problem E with k <= 10^18 i think bynary search value MIN and after i check how many value such as f(ai,p) — f(ai,p + 1) >= MIN for each Ai. If the number of value >= MIN no more than K then save it and increase MIN. O(Nlog(Ai)logK)
Is Bouncing Boomerangs' code solution in C++ correct? Because after running it I discovered a different answer. Following is the output that I encountered after executing it: 5 1 1 1 6 2 3 2 5 3 5 And the output expected is as follows: 5 2 1 2 5 3 3 3 6 5 6 Correct me if I am wrong.
Both outputs produce the array 2 0 3 0 1 1. They are both correct outputs and will both be accepted by the checker.
In 1428D, why is it preferred to chain-up the first 3 from the right, with a 2 and not 1? I mean, suppose 3 is paired with a 1, then why can't that 1 be used with some 2? Please explain.
UPD: I got it!
Your solution will pass even if you chain it with the nearest of 1 or 2 which is unchained , I did the same in my AC solution.
E is a nice problem, if you made $$$n, k \le 5000$$$, then $$$O(nk)$$$ trivial dp would pass. Thus, with $$$n, k \le 10^5$$$ it is actually a much nicer problem in my opinion.
can describe your O(nk) dp? I actually dont know how O(nk) dp would work here
I might be wrong but this is my thought process during the contest: there are $$$k - n$$$ "chances" to cut the carrots. Let $$$dp[i][j]$$$ be the best solution to use exactly $$$j$$$ chances on the first $$$i$$$ carrots. I think you should be able to find some recurrences over there. The final answer is going to be $$$dp[n][k - n].$$$
That ia trivial. But im not able to find O(1) transition.
O(logN) transition has many ways to do but not simple. One way is dnc. Another way is notice that sorting carrots in descending order, number of cuts is non decreasing, which gives us a (n)*(k-n)*(1/1+1/2+1/3+1/4+...) transition bound.
If you can figure out O(1) transition i would be happy to hear it :)
Oh my bad, I just realized my solution was actually $$$O(nk^2)$$$ lol.
My solution for F requires little thinking. (and little coding time since I wrote a similar code before and copied it...)
Just move $$$r$$$ from $$$1$$$ to $$$n$$$. Let $$$f_i$$$ be the answer for segment $$$[i,r]$$$.
If $$$a_r=0$$$, we don't do anything. (just add the sum of all $$$f$$$ to $$$ans$$$) Otherwise, let $$$lst$$$ be the minimum number that $$$a_{lst}\sim a_r$$$ are all $$$1$$$. Add $$$f_lst \sim f_r$$$ by $$$1$$$, and make $$$f_{1} \sim f_{lst-1}$$$ be the maximum one of themselves and $$$r-lst+1$$$.
Use a segment tree with lazy tags to handle range add and range chkmax. There's a well-known trick on maintaining the sum: maintain the number of minimums in the segment, the minimum in the segment and the second minimum in the segment. If the segment's minimum is greater than $$$k$$$ ($$$k$$$ is $$$r-lst+1$$$) then quit. If the minimum $$$x$$$ and the second minimum $$$y$$$ satisfy $$$x<k\le y$$$ then change the minimum and the count. Else brute force into its left and right sons. The upper bound of complexity is proved to be $$$O(n\log^2 n)$$$. (I don't know the exact complexity though)
Sorry for asking, but how does a O(TC*N) solution pass B as max test cases are 1000 and N is 300,000? Wouldn't that be 3*10^8 when 10^8 runs in 1 second?
Same goes for C.
Look at the bottom of Input section. Problem setter declared that It is guaranteed that the sum of n among all test cases does not exceed 300000. This means TC*N will be at most 300000.
How could we solve D with a[i] >= 4?
For 1428E, my approach was 1. Insert all elements into a max heap 2. Select the max element every time, and pop this out. Split this to two halves and insert back these halves into the heap. 3. Continue this till the size of the heap becomes k. But this approach turns out to be wrong. Can anyone tell me what is the issue ? Thanks in advance !!
The problem is if you are splitting an element into some parts it should be as even as possible. Suppose initially your heap contains 10 and k = 3. So you will split 10 into 5,5 and then to 2,3,5 whereas splitting into 3,3,4 will give you a better answer.
C++ Implementation of D is clever
Nice contest, i have learned a lot of things =)
People come to see tutorial if they couldn't managed to get the idea or solve the problem for any other reason. You guys should write the solution code as clean as possible. Using #define is useful for the contestants to minimize the code and time but not suitable for you as it makes the code much difficult to understand. Hope we will see #define less tutorial in the future:)
you can open other people's code. Setters focus on making sure the explanation in the editorial is clear.
Can anyone elaborate
Firstly, we notice that the contents of the stack do not actually matter. We actually only need to maintain the length of this stack. Decrementing the size of the stack whenever possible is optimal as it is the best we can do. And in the case where we must push B to the stack, this is optimal as the parity of the length of the stack must be the same as the parity of the processed string, so obtaining a stack of length 0 is impossble.for probem C?The (also acceptable) solution I did was maintain a stack of characters of 'A's and 'B's. Then I push each character and check the top two if it can be removed. Finally, I output the length of the stack.
The reason that the contents of the stack are unimportant is that if it is an 'A', you will always push it to the stack and if it's a 'B' you will always pop an element (as you can pop "AB and "BB") unless there are no elements on the stack.
PROBLEM E CARROTS FOR RABBITS COMMENTED CODE https://ide.geeksforgeeks.org/zsZx6svH3N
For problem F, can someone please explain the line that updates the cur in inner loop? "cur += (l-1+x) — hist[x]" What is it exactly doing & how is it correctly updating the tot?
Can you please explain bensonlzl dvdg6566?
The variable $$$cur$$$ stores the current area under the histogram and needs to be added to $$$tot$$$, which is the total sum of areas (aka the answer at the end).
Here we are considering the segment of 1s from $$$l$$$ to $$$r$$$ inclusive. Now we consider the $$$x$$$-th one in this segment of 1s. The total area this 1 adds is the distance from itself to the last index $$$i$$$ where the height of the histogram is $$$x$$$. You can look at the diagrams in the tutorial to convince yourself that this is true.
Thus, we need to add $$$l-1+x - hist[x]$$$ to the current area.
Now if we look what the histogram looks like after we added the entire segment of ones, the $$$x$$$-th 1 from the back is at index $$$r-x+1$$$, which means that the height of the histogram at this index $$$(r-x+1)$$$ after we have updated the entire segment of 1s is $$$x$$$, so we update $$$hist[x]$$$ accordingly.
I laughed out when I saw the code with language C++ for "1428E — Carrots for Rabbits". The Chinese characters in the beginning reminded me how popular the Chinese song was in the world some time ago.
Another(probably incorrect) solution for G.
Let $$$dp[mask][sum]$$$ be the answer for the problem when we are allowed to use only positions from $$$mask$$$ (e.g., if $$$mask = 100101_2$$$, our numbers can contain non-zero digits on positions $$$1, 100, 100000$$$).
Transition for this $$$dp$$$: $$$dp[mask][sum] ← dp[{mask} \oplus {2^{pos}}][sum - l \cdot 10^{pos}]$$$, where $$$l$$$ is the sum of digits, we put at position $$$pos$$$. $$$l_{max} = min ( 9k, \lfloor {{sum} \over {10^{pos}}}\rfloor)$$$ is the maximum possible value of $$$l$$$. Let's iterate $$$l$$$ from $$$l_{max} - MAGIC$$$ to $$$l_{max}$$$.
This $$$dp$$$ takes $$$O(2^6 \cdot 6 \cdot n \cdot MAGIC)$$$ to calculate, so let's do meet-in-the-middle: calculate $$$dp_1$$$ for the lowest $$$3$$$ positions and $$$dp_2$$$ for the highest $$$3$$$ positions. Now it takes $$$O(2^3 \cdot 3 \cdot n \cdot MAGIC)$$$ to calculate.
Answer for $$$n$$$ is maximum of $$$dp_2[allPositions][i] + dp_1[allPositions][n - 10^3 \cdot i]$$$.
Total complexity is $$$O(2^3 \cdot 3 \cdot n \cdot MAGIC + q \cdot 10^3)$$$.
For some reason it passes for $$$MAGIC = 30$$$.
Someone please explain why simple binary search doesnt work for E? I ran Binary Search on the biggest size of carrot, and for each carrot, computed how many carrots it needs to be split so that largest piece cannot be larger than mid, and then split this carrot as evenly as possible. But this is not working.
The code is below:
Got it, its just wrong. We may also consider example case $$$n = 2, k = 5$$$, $$$a = [20, 60]$$$ then there is no way to get all sizes less than a value x and number of pieces exactly 5.
+1 for the input.
My solution for problem F is very different and am proud of myself to proved it, coded it up, and got it accepted! I became surprise when I saw the solution of the author.
Here is my code: https://codeforces.com/contest/1428/submission/115365132.
Just a short explanation of my solution: Draw a table (on a paper), where rows are the index of strings, and each column (from 0 to n) shows the number of continuous ones if we end at index r (at row r). If you fill out the table on the paper, you'll see when we have a '0' or '1' in the string, how the values for each row changes, which highly depends on the values in the previous row.
The solution runs in O(n log n) and uses segment tree + lazy propagation technique.
How to solve Problem E Carrot for rabbits with k<=1e18 . Original version is very good but curious to know the solution for larger contraints.