If d = 0, the there is the only number with 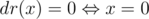 , so, if k = 1, the answer is 0, otherwise — No solution.
, so, if k = 1, the answer is 0, otherwise — No solution.
If d > 0, then one of correct numbers is d × 10k - 1.
Time complexity: O(1) + O(k) for the output.
355B - Vasya and Public Transport
If we buy a ticket of the fourth type, we don't have to buy anything else, so, the answer is min(c4, answer using tickets of first three types).
Now, when we don't have ticket of the fourth type, we can solve the task separately for buses and trolleys.
Solving the problem only for buses: if we buy a ticket of the third type, we don't have to buy anything else, so, the answer is min(c3, answer using tickets of first two types).
Without tickets of type three, we can solve the problem separately for each bus. If we buy a ticket of the second type, we will spend c2 burles and if we buy ai tickets of the first type, we will spend (ai × c1) burles. So, the answer for bus i is min(c2, ai × c1).
Now it is not difficult to obtain the following solution:
function f(x, k) {
res = 0;
for i = 1 .. k
res = res + min(c2, x[i] * c1);
return min(c3, res);
}
ans = min(c4, f(a, n) + f(b, m));
Time complexity: O(n + m).
Brute force how many times we will use operation from the left. So, if we use it k times, then it's clear, that we will take first k items by the left operations and last (n - k) items by the right operations. So, robot will spend sumLeft[k]·l + sumRight[n - k]·r energy plus some penalty for the same operations. To minimize this penalty we should perform the operations in the following order LRLRL ... RLRLLLLL ..., starting from the bigger set. For example, if k = 7, n - k = 4, we should perform operations in this order: LRLRLRLRL LL. So, we will have to pay the penalty two times (7 - 4 - 1).
sumLeft[i] — sum of first i weights, sumRight[i] — sum of last i weights.
Solution in pseudocode:
ans = inf;
for i = 0 .. n {
curr = firstSum[i] * l + lastSum[n-i] * r;
if ( i > n - i ) curr = curr + (2i - n - 1) * Ql;
if ( i < n - i ) curr = curr + (n - 2i - 1) * Qr;
ans = min(ans, curr);
}
Time complexity: O(n).
We will say that cell (r, c) corresponds to a string s, if there exist correct path, which ends in the cell (r, c) and this path corresponds to a string s.
Let call a set of cells which corresponds to some string s a state. One state can correspond to different strings. We can't brute force all possible strings, because their count — 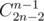 is too big, but we can brute force all possible states. It's not hard to observe that all cells that corresponds to some string s lies on same diagonal, so the total count of states is 21 + 22 + ... + 2n - 1 + 2n + 2n - 1 + ... + 22 + 21 = O(2n). In implementation we can denote state with diagonal number (from 1 to 2n - 1) and bitmask of cells corresponding to this state (2n).
is too big, but we can brute force all possible states. It's not hard to observe that all cells that corresponds to some string s lies on same diagonal, so the total count of states is 21 + 22 + ... + 2n - 1 + 2n + 2n - 1 + ... + 22 + 21 = O(2n). In implementation we can denote state with diagonal number (from 1 to 2n - 1) and bitmask of cells corresponding to this state (2n).
From each state we can move to 26 different states (actually less) and all possible moves depends on the state, not on the string. On the image you can see an example of move: from state, which is highlighted in blue by letter a we will move to the state, which is highlighted in yellow.

Now, for each state we can calculate a value of (count of letters A - count of letters B) in the string, starting from this state. If at the moment is first players turn (an even diagonal), we have to maximize this value, otherwise — minimize. It can be implemented as recursion with memoization.
The winner can be determined by the value of state, which corresponds to the single cell (1, 1).
Complexity: O(2n × (n + alpha)), where alpha is the size of alphabet.
354C - Vasya and Beautiful Arrays
The problem was to find greatest d, such that ai ≥ d, ai mod d ≤ k holds for each i.
Let m = min(ai), then d ≤ m. Let consider two cases:
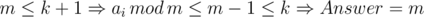
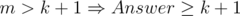 . In this case we will brute force answer from k + 1 to m. We can check, if number d is a correct answer in the following way:
. In this case we will brute force answer from k + 1 to m. We can check, if number d is a correct answer in the following way:
We have to check that ai mod d ≤ k for some fixed d, which is equals to 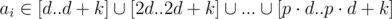 , where
, where 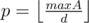 . Since all these intervals [x·d..x·d + k] doesn't intersects each with other, we can just check that
. Since all these intervals [x·d..x·d + k] doesn't intersects each with other, we can just check that 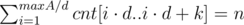 , where cnt[l..r] — count of numbers ai in the interval [l..r].
, where cnt[l..r] — count of numbers ai in the interval [l..r].
Time complexity: O(maxA log maxA), proof is based on the sum of harmonic series.
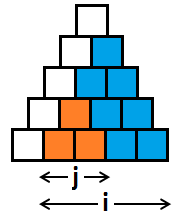
This tasks is solvable with dynamic programming. First of all let consider solution with complexity O(n3).
Let dp[i][j] be the answer for the highlighted in blue part (minimal cost of transferring all special cells that lies inside this area). Then dp[n][0] will be the answer for our original problem.
How to recalculate such DP? It's clear that in the leftmost column (inside the blue area) we will choose at most one cell as the top of some subpyramid. If we choose two, then the smallest one will lie fully inside the biggest one (as the orange subpyramid lies inside the blue one). Now, let brute force the cell, which will be the top of subpyramid in this column in time O(n) and we will obtain the following transition:
To simplify the formulas, let assume that 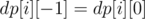 .
.
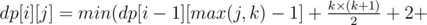
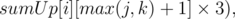 0 ≤ k ≤ i, where k is the height on which we will choose our top cell, or 0, if we don't choose any subpyramid in this column. sumUp[i][p] — count of special cells in the i-th column at height starting from p, this cells we will have to transfer one by one, using the first type operations.
0 ≤ k ≤ i, where k is the height on which we will choose our top cell, or 0, if we don't choose any subpyramid in this column. sumUp[i][p] — count of special cells in the i-th column at height starting from p, this cells we will have to transfer one by one, using the first type operations.
We can reduce the complexity by one n, if we will recalculate out DP in the following way:
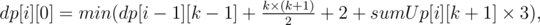 0 ≤ k ≤ i;
0 ≤ k ≤ i;
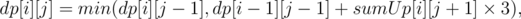 for all j > 0.
for all j > 0.
The proof that this is correct is quite simple and is left to the reader. :)
Also, we can observe that it is not profitably to take some subpyramid with height greater than 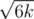 , because for such subpyramid we will pay > 3k, but if we transfer all cells using the first type operations we will pay only 3k. So, the second dimension (j) in out DP can be reduced to
, because for such subpyramid we will pay > 3k, but if we transfer all cells using the first type operations we will pay only 3k. So, the second dimension (j) in out DP can be reduced to 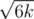 .
.
Also, to receive AC, you should store only last 2 layers of the DP, otherwise there will be not enough memory.
Time complexity: 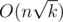 .
.
354E - Lucky Number Representation
Author's solution, much more complicated than suggested by many participants during the competition, easy solution will be described below.
First of all, let write a DP with complexity O(N * lucky_count(N)), where lucky_count(N) is the count of lucky numbers ≤ N, lucky_count(10n) = 3n. As we can see, for all sufficiently large N solution exists. Really — for every N > 523.
Now, we can say that for N ≤ 10000 we have a solution, which is found using DP. Let's solve the task for larger values of N.
Next and key idea is to separate the task into two parts: N = N1 + N2. Let's choose N1 and N2 in such way that for them it was easy to find a solution and then merge these two solutions into one. Let N1 = N mod 4000, N2 = N - N1. Here we can have a problem that there is no solution for number N1, in this case we can do N1 = N1 + 4000, N2 = N2 - 4000.
Now it is guaranteed that solutions exists for both N1 and N2, moreover, the solution for number N1 will contain only numbers of not more than 3 digits ( < 1000). The proof is quite easy: if N1 < 4000 — it is obvious; else — if the solution uses some number of the form (4000 + some_lucky_number), we can replace it with just some_lucky_number and receive a correct solution for number (N1 - 4000), but is doesn't exist!
So, the solution for number N1 we have found using DP, now let's find the solution for N2. If it will contains only of numbers of the form (some_lucky_number × 1000), then we will be able to easily merge this solution with solution for N1, so, let's find such a solution. Here we will use the fact that N2 is divisible by 4. For simplicity, let's divide N2 by 1000 and in the end multiply all Ans2(i) by the same 1000. Let P = N2 / 4. Now, let's construct the solution. Consider, for example, P = 95: we will walk through digits of this number, last digit — 5, means that we want to put digit 4 at the last decimal position of five answer numbers — ok, put it and in the last, sixth, number leave there digit 0. Go forward, digit 9 — we don't have nine numbers, but we can replace seven fours with four sevens, then to the second position we have to put (9 - 7) fours and 4 sevens, in total — 6 numbers, exactly as much as we have.
Thus, if next digit d ≤ 6, we just put to the first d answer numbers digit 4 to the next position; if d > 6, then we put 4 sevens and (d - 7) fours. In all other numbers we just leave digit 0 at this position.
If Ans1(i) — answer for N1, Ans2(i) — for N2, the the answer for N will be just Ans(i) = Ans1(i) + Ans2(i).
Time complexity for one number: O(logN).
During the competition many participants have wrote the following solution:
dp[i][j] — can we put the digit to the last i decimal positions of the answer number in such way that we will get correct last i digits in the sum and with carry to the next position equals to j. Then the solution exist iff dp[19][0] = true. To restore the answer we just have to remember for each state the previous state. Base — dp[0][0] = true. Transition — brute force how many fours and sevens we will put to the i-th position.











GOOD!
You can use Google to translate it into English.
I will try to translate it today.
Not able to understand anything related to "354B — Game with Strings". Can anyone provide a simpler explanation and a reference solution?
Can someone please explain the question Vasya and Beautiful Arrays ????
Can someone please explain Problem C : Vasya and Beautiful Arrays again?
My thoughts is like this:
Let m be the minimum numeber in A, which is the maximum possible ans
so if m <= k+1, m is the answer
for m > k+1, we have to brute force answer from k+1 to m,
for easy understanding actually we can brute force from 1 to m
Let d be the current testing answer, 1<=d<=m
For a specific d, we have to check if where
where 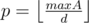 It can be achieve by something like partial sum, using O(p) = O(maxA / d)
It can be achieve by something like partial sum, using O(p) = O(maxA / d)
so in total it's O(maxA/1 + maxA/2 + ... + maxA/m)
= O(maxA * (1+1/2+...+1/maxA)) //m can be as large as maxA
= O(maxA * ln(MaxA)) //from wiki, partial sum of harmonic series
Hi. Would you please help me to clarify why k+1 is chosen?
Why k+1 is the boundary compared to m?
Thanks
I think we can think this way:
1. m = min (A) is the maximum possible answer we can get
2. x is a possible solution iff a_i % x <= k for all i
3. For any positive number c, c% (k+1) <= k
if m <= k+1, for any positive number c, c%m <= k (by 3)
a_i % m <= k for all i (by 2)
m is a possible solution, also the maximum one (by 1)
How do we implement summation(i=K+1,i=max A/d)cnt(i*d,i*d+k)=n in 354C??
We can precalculate partial sums:
cnt[i] = count of numbers ≤ i we have in array a.Now, this summation can be implemented just like this:
I think, this solution 4770602 is quite clear to understand it.
For "Game with strings": Can someone explain to me why "5 cbbbb bcbbb aacbb aaacb aaaac " gives the first player as the winner? He has to start on 'c' and then is dragged by the second player on the right side of the main diagonal. The best player 1 can obtain is "cbcbcbcbc" which is a clear defeat for him.
After first 2 moves the string will be "cb" (the only good string of length 2). Then the first player can extend it to "cba". "cba" is a good string, because of path [(1, 1), (2, 1), (3, 1)]. Now, first player can always write letter "a" and obtain string "cbaaaaaac" in the end. So, the answer is FIRST.
One move in this game is just writing one letter to the end of string, but not moving to some cell. These two games are not equivalent!
i have a question about d problem.
5 cbbbb bcbbb aacbb aaacb aaaac
in this input. the jury's answer is "first". but i think the answer should be "second". i will explain it;
note that the player are playing optimally.
1.step — the first player chooses (1,1) cell that is only option. (a = 0, b = 0) 2.step — the second player chooses (1,2) because if he goes down he will lose.(a = 0, b = 1) 3.step — the first player chooses (2,2) because if he goes right it is obvious that he will already lose.(a = 0, b = 1) 4.step — the second player chooses (2,3).(a = 0, b = 2) 5.step — the first player chooses (3,3).(a = 0, b = 2) 6.step — the second player chooses (3,4).(a = 0, b = 3) 7.step — the first player chooses (4,4).(a = 0, b = 3) 8.step — the second player chooses (4,5).(a = 0, b = 4) 9.step — the first player chooses (5,5).(a = 0, b = 4)
so the second player wins.
can any one explain that why answer is "first" ?
can anyone explain please ?
The comment just above yours asks exactly the same question and has an answer.
In A, if we have been asked to find the number of solutions which has digits k and sum d. Then can we find the solution or not? If yes, then what are the solutions and their time complexity? Please someone help on this.