Disclaimer: I will not promise that this blog will make you code lca better. binary lifting is generally better than the following algorithm and i am only sharing it since i find it very interesting.
===================================================================================
intro (skip this if you know what lca is)
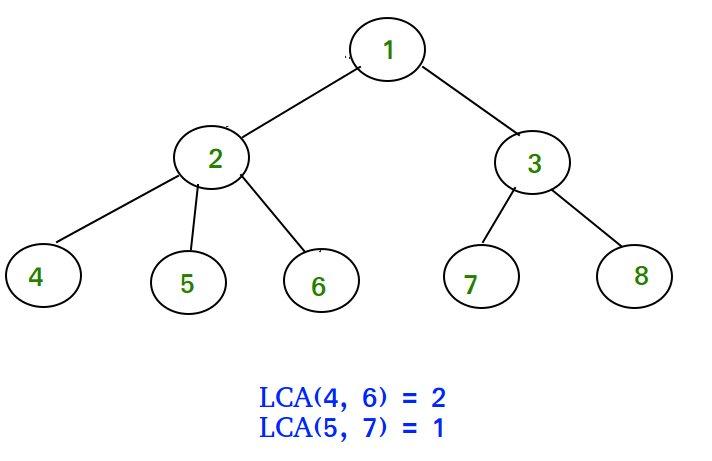
if you didnt know, lca stands for least common ancestor (and implies a rooted tree). so any ancestor of a node u. is any node on u's path to the root node (including the root itself). in the diagram below nodes 1 and 2 are both ancestors of node 4. so common ancestors of nodes u and v are the nodes that are both ancestors of u and ancestors of v. the least common ancestor of nodes u and v is first node that u and v share as an ancestor (first meaning the ancestor with the largest depth). and you can see in the picture below the lca of 4 and 6 is 2, since that's the node with the furthest depth from the root that is both an ancestor of u and an ancestor of v. 1 does not count as the lca since 2 is further down and 5 does not count since it is not an ancestor of 4 (or 6 for that matter). for any pair of nodes on a rooted tree there is only one lca (hopefully this is intuitive), and this blog post describes ways to find that lca.
here is an image (from google search) of a tree. remember lca only works on a rooted tree since you have a sense of "up" and "down" only if there is a root
Sqrt LCA
imagine if we had a function k_up where k_up(u, k) returns the k'th node up from u. so from the diagram above k_up(2, 1) is 1 and k_up(8, 2) is also 1. this will be very helpful to do lca as we will see later. the array par[] stores for each u the direct parent of u (the parent of the root node is an imaginary node, 0 or -1 depending upon your implementation). in the diagram above par[2] = 1, par[5] = 2, and par[8] = 3.
so in all of the following code assume the par array is already calcutated, as for how to calculate it.... go google it.
int k_up(int u, int k){
for(int i = 0; i<k; i++){
u = par[u];
}
return u;
}
so what is the complexity of the above code? its O(k) since you loop over k to find par[u] k times. darn that's slow. i really wish we could do that faster. well that's the point of this blog.
so now lets pick a define a constant R, all we have to know abt R is that it's a constant <= the number of nodes on the tree. now for each u we define super[u] as the parent of u R times up (super for superparent, i love that word "superparent"). in the case that going k times from u takes us higher than the tree allows supor[u] = -1. so how does this help? so now in k_up(u, k) we can first loop over floor(k/R) times the superparent then we loop over k%R times on the parent array. so in total we move up floor(k/R)*R + k%R times (or k times :OOO). now the complexity is reduced to O(k/R + R) since the first half can only take k/R turns at most and the second half can take R steps at most. below is some code of the idea
int k_up(int u, int k){
while(k >= R) k = k-R, u = super[u];
for(int i = 0; i<k; i++) u = par[u];
return u;
}
now there are a few problems, namely how to find super[] and what is R, If we set R to be sqrt(n), O(k/R + R) is minimized. (hopefully the intuition makes sense), in fact picking R like this is so common its even got a name: "SQRT decomp". and to find super, you can for each u, loop up R times to find the parent R steps up. you can do this even faster, but im too lazy to cover that.
be sure you understand all of this since the concept of a k_up function will come up a lot later in this blog.
now onto the actual lca part. so consider a rooted tree and any two nodes u and v that are on the same level or have the same distance from the root. if we just marched from each node taking 1 step from each at the same time, the first node where they are the same is their lca. (note this only works if u and v start on the same level). so below is an implementation of the idea
int lca(int u, int v){ //remember that they have the same depth
while(u != v){
u = par[u], v = par[v];
}
return u;
}
so whats the complexity of this code? its O(d) where d is the difference of depth from the lca to node u (or v). this at worst case can be O(n) where n is the number of nodes in the tree (imagine a chain). so what can we do to speed it up? let us refer to the super array again. so if super[u] == super[v] then we know that the lca of u and v has to be super[u] or further down the tree. since if it was further up, we'd just take super[u] instead since super[u] is an ancestor of u and super[v] is an ancestor of v (and they are the same :O). so now (remember nodes u and v have the same depth) we can just loop over the super[u] and super[v] while they are different, and when they are the same, we'll loop over the parent array. below is the code for this idea.
int lca(int u, int v){ //remember that they have the same depth
while(super[u] != super[v]){
u = super[u], v = super[v];
}
while(u != v){
u = par[u], v = par[v];
}
return u;
}
what is the complexity of the above code? its O(n/R + n%R) worst case. which is also O(sqrt(n)) since R is sqrt(n). sadly this only find the lca when the two nodes have the same depth from the root. luckily this is where our k_up function comes in handy. so if we define dep[u] as the depth of node u from the root and dep[root] = 1, then we can just set u to be the further down node out of u and v and then make u = k_up(u, dep[u] — depv]). and now it becomes lca on the same depth. below is the implementation of the idea.
int k_up(int u, int k){
while(k >= R) k = k/R, u = super[u];
for(int i = 0; i<k; i++) u = par[u];
return u;
}
int lca(int u, int v){
if(dep[u] < dep[v]) swap(u, v); //setting u to be the node with greater depth
u = k_up(u, dep[u] - dep[v]); //moving u up to the same level at v
while(super[u] != super[v]){ //iterating over super
u = super[u], v = super[v];
}
while(u != v){ //ieterating over par
u = par[u], v = par[v];
}
return u; //u and v will be the same, so returnv works too
}
since k_up is also O(root(n)) worst case, the. overall query is still O(root(n)) in time complexity.
and our lca implemention is complete! its O(n sqrt(n)) precomp (or O(n) if you are smart abt it, try figuring out how later :D) and its O(sqrt(n)) per query. a more complete implementaion can be found here (along with calculating the par, super, and dep arrays).
Conclusion
the overall time complexity is O((n+q)sqrt(n)) and the memory is O(n) since we just have to store par, super, and dep arrays. but if you squish the code, it becomes a pretty short impl (and slow) and you can make the compleixty O(n + q*sqrt(n)) if you want.
please remember O(sqrt(n)) for lca queries is really slow. reaaallllly slow. there are better lca algorithms but this is cool one i wanted to introduce. also note the actually fun lca algorithm (that's not bin lifiting) will be on the next blog post since this one got too long. rip.
thank you reading and i apologize for any typos, instances of unclearness, and bugs in the code.











Auto comment: topic has been updated by willy108 (previous revision, new revision, compare).
Auto comment: topic has been updated by willy108 (previous revision, new revision, compare).