Блог пользователя my_tempo

Problem : Constructing Tests
Автор my_tempo, история, 3 года назад, По-английски

Problem Link
I think it would be optimal to fill zeros starting from (m,m) and then at a gap of 2*m-2 in each row(because we will cover that much squares of size m*m).
So the minimum zeros required would be around n/(2*m-1)
Same will happen for columns, So the answer should be somewhere around (n/(2*m-1))^2 after just taking care of n%(2m-1) remaining cells.
But on the editorial, It is saying that minimum number of zeros should be (n/m)^2, Can someone tell where am I going wrong?

  • Проголосовать: нравится
  • +6
  • Проголосовать: не нравится

»
3 года назад, # |
  Проголосовать: нравится +1 Проголосовать: не нравится

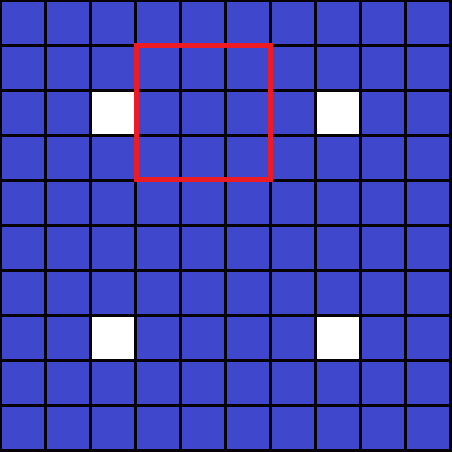
A picture here is very instructive (below with N=10 and M=3).

Here it's easier to just think about this as starting from the top left corner and placing MxM tiles with a white square in the bottom right. Here the 10th row and column don't fit, but since the white square has a reach of M-1, it doesn't matter. For that reason it follows that formula can just be floor(N/M)^2.

The way you want to tile it forgets about some regions:

→ Ответить