Task B. T-shirts from sponsor.
Enumerate sizes of t-shirts by integers from 0 to 4. For each size we store the number of t-shirts of this size left. To process each participant, we need to determine the number of his preferable size. Then we iterate over all possible sizes and choose the most suitable one (with the nearest number) among the sizes with non-zero number of t-shirts left.
Task D. Parking.
Lets keep a set of cars which are currently parked. In this problem it is not essential how to keep this set. For each car, store its length and position. To process a request of type 2, we need to find the car which should leave the parking and remove it from the set. To do this, we should enumerate the cars and get the car number by the number of request. Now consider a request of type 1. As the drives tries to park his car as close to the beginning of the parking slot as possible, we can reduce the set of reasonable positions for parking: include into this set the beginning of the parking and all positions that are exactly b meters after the front of some car. For every position in this set we should determine if it is possible to park car in it. Then we choose the closest to the beginning position among admissible ones.
Task E. Comb.
Denote the input matrix by a. Compute the partial sums in each row first: 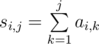 . All these sums can be easily computed in O(nm). Then solve the task using dynamic programming. By di, j denote the maximum sum of numbers that we can take from first i rows, taking exactly j numbers in row i and not violating the "comb" condition. Starting values are obvious d1, j = s1, j. Transitions for i > 1 looks like this:
. All these sums can be easily computed in O(nm). Then solve the task using dynamic programming. By di, j denote the maximum sum of numbers that we can take from first i rows, taking exactly j numbers in row i and not violating the "comb" condition. Starting values are obvious d1, j = s1, j. Transitions for i > 1 looks like this:
1) If i is even, 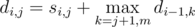 .
.
2) If i is odd, 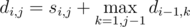 .
.
Straightforward computing of values di, j by these formulas has complexity O(nm2), which is not suitable. Use the following fact: if we compute values di, j in order of decreasing j in case of even i and in order of increasing j in case of odd i, the maximum values of di - 1, k from the previous row can be computed in O(1), using value for previous j, i.e. without making a cycle for computation. This solution has complexity O(nm) and passes all tests.











I followed the DP showed here, but I keep getting WA! :( I was WAing in testcase 2 at first, and then I realised the bug is that i used %lld instead of %I64d. However, even after I changed that, I still get WA for testcase 3 :(. Can someone help me?
My code is shown below:
http://pastebin.com/yZJje5KZ
EDIT: Oops sorry, forgot to mention which question I was talking about. I am trying to solve Comb.
the answer may be negtive
EDIT: Oh ok, I got what you meant. Thanks!