Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
def maxSum(x):
return x ** 2
def getAns(x):
res = 1
while maxSum(res) < x:
res += 1
return res
def main():
t = int(input())
for i in range(t):
print(getAns(int(input())))
main()
Idea: Neon
Tutorial
Tutorial is loading...
Solution (Neon)
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
while (t--) {
int n, a, b;
string s;
cin >> n >> a >> b >> s;
int m = unique(s.begin(), s.end()) - s.begin();
cout << n * a + max(n * b, (m / 2 + 1) * b) << '\n';
}
}
Idea: adedalic
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
#define x first
#define y second
typedef long long li;
typedef long double ld;
typedef pair<li, li> pt;
const int INF = int(1e9);
const li INF64 = li(1e18);
const ld EPS = 1e-9;
int n;
vector<li> a;
inline bool read() {
if(!(cin >> n))
return false;
a.resize(n);
fore (i, 0, n)
cin >> a[i];
return true;
}
li d(const pt &a, const pt &b) {
return abs(a.x - b.x) + abs(a.y - b.y);
}
inline void solve() {
li ans = 0;
fore (i, 0, n) {
fore (j, i, n) {
if (i + 2 <= j) {
bool ok = true;
fore (i1, i, j) fore (i2, i1 + 1, j) {
if (d(pt(a[i1], i1), pt(a[j], j)) == d(pt(a[i1], i1), pt(a[i2], i2)) + d(pt(a[i2], i2), pt(a[j], j)))
ok = false;
}
if (!ok)
break;
}
ans++;
}
}
cout << ans << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
int t; cin >> t;
while(t--) {
read();
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Idea: adedalic
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
const int MOD = int(1e9) + 7;
int norm(int a) {
while (a >= MOD)
a -= MOD;
while (a < 0)
a += MOD;
return a;
}
int mul(int a, int b) {
return int(a * 1ll * b % MOD);
}
int binPow(int a, int k) {
int ans = 1;
while (k > 0) {
if (k & 1)
ans = mul(ans, a);
a = mul(a, a);
k >>= 1;
}
return ans;
}
const int N = 200 * 1000 + 55;
int f[N], inf[N];
void precalc() {
f[0] = inf[0] = 1;
fore (i, 1, N) {
f[i] = mul(f[i - 1], i);
inf[i] = binPow(f[i], MOD - 2);
}
}
int C(int n, int k) {
if (k < 0 || n < k)
return 0;
return mul(f[n], mul(inf[n - k], inf[k]));
}
int n, l, r;
inline bool read() {
if(!(cin >> n >> l >> r))
return false;
return true;
}
inline void solve() {
int half = n / 2;
int st = min(1 - l, r - n);
int ans = mul(st, C(n, half));
if (n & 1)
ans = norm(ans + mul(st, C(n, half + 1)));
for (int k = st + 1; ; k++) {
int lf = max(1, l + k);
int rg = min(n, r - k);
if (rg + 1 - lf < 0)
break;
ans = norm(ans + C(rg + 1 - lf, half - (lf - 1)));
if (n & 1)
ans = norm(ans + C(rg + 1 - lf, half + 1 - (lf - 1)));
}
cout << ans << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
precalc();
int t; cin >> t;
while (t--) {
read();
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (awoo)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
int n, k;
string s;
bool check(int d){
vector<int> lst(k, n);
vector<vector<int>> pos(n + 1, vector<int>(k, n + 1));
for (int i = n - 1; i >= 0; --i){
if (s[i] != '?'){
lst[s[i] - 'a'] = i;
}
int cur = n;
forn(j, k){
pos[i][j] = (i + d <= cur ? i + d : pos[i + 1][j]);
cur = min(cur, lst[j]);
}
cur = n;
for (int j = k - 1; j >= 0; --j){
if (i + d > cur) pos[i][j] = pos[i + 1][j];
cur = min(cur, lst[j]);
}
}
vector<int> dp(1 << k, n + 1);
dp[0] = 0;
forn(mask, 1 << k) if (dp[mask] < n + 1){
forn(i, k) if (!((mask >> i) & 1))
dp[mask | (1 << i)] = min(dp[mask | (1 << i)], pos[dp[mask]][i]);
}
return dp[(1 << k) - 1] <= n;
}
int main() {
cin >> n >> k;
cin >> s;
int l = 1, r = n;
int res = 0;
while (l <= r){
int m = (l + r) / 2;
if (check(m)){
res = m;
l = m + 1;
}
else{
r = m - 1;
}
}
cout << res << endl;
return 0;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution 1 (awoo)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int INF = 1e9;
struct edge2{
int u, w;
};
vector<vector<edge2>> g;
struct edge3{
int v, u, w;
};
bool operator <(const edge3 &a, const edge3 &b){
if (a.w != b.w)
return a.w < b.w;
if (min(a.v, a.u) != min(b.v, b.u))
return min(a.v, a.u) < min(b.v, b.u);
return max(a.v, a.u) < max(b.v, b.u);
}
vector<vector<int>> comps;
vector<int> p;
bool unite(int a, int b){
a = p[a], b = p[b];
if (a == b) return false;
if (comps[a].size() < comps[b].size()) swap(a, b);
for (int v : comps[b]){
p[v] = a;
comps[a].push_back(v);
}
comps[b].clear();
return true;
}
vector<int> mn;
void dfs(int v, int p, int d){
mn[v] = d;
for (auto e : g[v]) if (e.u != p)
dfs(e.u, v, max(d, e.w));
}
int main() {
int n, q, s, d;
scanf("%d%d%d%d", &n, &q, &s, &d);
--s;
vector<int> a(n);
forn(i, n) scanf("%d", &a[i]);
vector<int> idx(a[n - 1] + 1);
forn(i, n) idx[a[i]] = i;
comps.resize(n);
p.resize(n);
forn(i, n) comps[i] = vector<int>(1, i), p[i] = i;
g.resize(n);
set<int> pos(a.begin(), a.end());
int cnt = n;
while (cnt > 1){
vector<edge3> es;
for (const vector<int> &comp : comps) if (!comp.empty()){
for (int i : comp)
pos.erase(a[i]);
edge3 mn = {-1, -1, INF};
for (int i : comp){
for (int dx : {-d, d}){
auto it = pos.lower_bound(a[i] + dx);
if (it != pos.end())
mn = min(mn, {i, idx[*it], abs(abs(a[i] - *it) - d)});
if (it != pos.begin()){
--it;
mn = min(mn, {i, idx[*it], abs(abs(a[i] - *it) - d)});
}
}
}
for (int i : comp)
pos.insert(a[i]);
assert(mn.v != -1);
es.push_back(mn);
}
for (auto e : es){
if (unite(e.v, e.u)){
--cnt;
g[e.v].push_back({e.u, e.w});
g[e.u].push_back({e.v, e.w});
}
}
}
mn.resize(n);
dfs(s, -1, 0);
forn(_, q){
int i, k;
scanf("%d%d", &i, &k);
--i;
puts(mn[i] <= k ? "Yes" : "No");
}
return 0;
}
Solution 2 (awoo)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int INF = 1e9;
struct edge2{
int u, w;
};
vector<vector<edge2>> g;
struct edge3{
int v, u, w;
edge3(){}
edge3(int v, int u, int w) : v(v), u(u), w(w) {
if (v > u) swap(v, u);
}
};
bool operator <(const edge3 &a, const edge3 &b){
if (a.w != b.w)
return a.w < b.w;
if (a.v != b.v)
return a.v < b.v;
return a.u < b.u;
}
vector<int> p, rk;
int getp(int a){
return a == p[a] ? a : p[a] = getp(p[a]);
}
bool unite(int a, int b){
a = getp(a), b = getp(b);
if (a == b) return false;
if (rk[a] < rk[b]) swap(a, b);
rk[a] += rk[b];
p[b] = a;
return true;
}
vector<int> mn;
void dfs(int v, int p, int d){
mn[v] = d;
for (auto e : g[v]) if (e.u != p)
dfs(e.u, v, max(d, e.w));
}
int main() {
int n, q, s, d;
scanf("%d%d%d%d", &n, &q, &s, &d);
--s;
vector<int> a(n);
forn(i, n) scanf("%d", &a[i]);
p.resize(n);
rk.resize(n);
forn(i, n) rk[i] = 1, p[i] = i;
g.resize(n);
int cnt = n;
int iter = 0;
while (cnt > 1){
++iter;
vector<edge3> es(n, edge3(-1, -1, INF));
int j, mn1, mn2;
j = 0, mn1 = -1, mn2 = -1;
forn(i, n) getp(i);
forn(i, n){
while (j < n && a[i] - a[j] > d){
if (mn1 == -1 || p[mn1] == p[j])
mn1 = j;
else{
mn2 = mn1;
mn1 = j;
}
++j;
}
if (mn1 != -1 && p[mn1] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn1, i, abs(abs(a[i] - a[mn1]) - d)));
}
if (mn2 != -1 && p[mn2] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn2, i, abs(abs(a[i] - a[mn2]) - d)));
}
}
j = 0, mn1 = -1, mn2 = -1;
forn(i, n){
while (j < n && a[j] - a[i] <= d){
if (mn1 == -1 || p[mn1] == p[j])
mn1 = j;
else{
mn2 = mn1;
mn1 = j;
}
++j;
}
if (mn1 != -1 && p[mn1] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn1, i, abs(abs(a[i] - a[mn1]) - d)));
}
if (mn2 != -1 && p[mn2] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn2, i, abs(abs(a[i] - a[mn2]) - d)));
}
}
j = n - 1, mn1 = -1, mn2 = -1;
for (int i = n - 1; i >= 0; --i){
while (j >= 0 && a[j] - a[i] > d){
if (mn1 == -1 || p[mn1] == p[j])
mn1 = j;
else{
mn2 = mn1;
mn1 = j;
}
--j;
}
if (mn1 != -1 && p[mn1] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn1, i, abs(abs(a[i] - a[mn1]) - d)));
}
if (mn2 != -1 && p[mn2] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn2, i, abs(abs(a[i] - a[mn2]) - d)));
}
}
j = n - 1, mn1 = -1, mn2 = -1;
for (int i = n - 1; i >= 0; --i){
while (j >= 0 && a[i] - a[j] <= d){
if (mn1 == -1 || p[mn1] == p[j])
mn1 = j;
else{
mn2 = mn1;
mn1 = j;
}
--j;
}
if (mn1 != -1 && p[mn1] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn1, i, abs(abs(a[i] - a[mn1]) - d)));
}
if (mn2 != -1 && p[mn2] != p[i]){
es[p[i]] = min(es[p[i]], edge3(mn2, i, abs(abs(a[i] - a[mn2]) - d)));
}
}
for (auto e : es) if (e.v != -1){
if (unite(e.v, e.u)){
--cnt;
g[e.v].push_back({e.u, e.w});
g[e.u].push_back({e.v, e.w});
}
}
}
mn.resize(n);
dfs(s, -1, 0);
forn(_, q){
int i, k;
scanf("%d%d", &i, &k);
--i;
puts(mn[i] <= k ? "Yes" : "No");
}
return 0;
}










Nice Editorial!
Thanks for good Editorial and solutions. Problem C was lovely to thinking on)
Non-graph solution to F:
Since the maximum coordinate is at most $$$10^6$$$, so long as we process each square a small number of times, we're good. Let's say we have a set of all squares that are reachable with some range value $$$k$$$. What new squares will we be able to reach when $$$k$$$->$$$k+1$$$? Those squares which we haven't yet reached, and are neighbors of some square in our set. On top of that, we might reach some rocks, which will be able to reach an interval of squares at distances $$$[d-k,d+k]$$$ from it.
So, let's keep a set of all edge squares — those that are not yet reachable with current value $$$k$$$, but are neighbors of a reachable square. In each step of increasing $$$k$$$, we will process all edge squares, mark them as reachable, and check their two neighbors — at most one of them might be a new edge square. If the edge square is a rock, we add it to our unprocessed rock stack.
Then, process all rocks while we have some left: find all unprocessed squares that are a distance of $$$[d-k, d+k]$$$ from it (if this finds more rocks, add them to the stack). We can do this operation by using a segment tree which keeps track of how many unprocessed squares are in any interval. If we query to process squares in $$$[L,R]$$$, and there are none, we just return, otherwise we recurse into the two subtrees that make it up. Everytime we reach a leaf of the tree, we process the square it represents, and will never visit it again, so across all these rock-queries we will process $$$O(X)$$$ squares each taking $$$O(logX)$$$ time, where X is the size of the coordinates. After we're done with all the rocks, we look at the neighbors of all the new squares we managed to reach, and add new edge squares to our set.
In the end, we process each square a constant number of times, and processing a square takes $$$O(logX)$$$ (getting to its leaf node in the segment tree/adding it to set).
We can either mark for each rock the $$$k$$$ that we needed to reach it and stop when all rocks are marked, or sort queries by their $$$k$$$ and answer them as we increase $$$k$$$, and once all queries are answered, sort them by index and print their answers.
The time complexity is $$$O(n+XlogX+q)$$$.
Submission (sorry for the slight mess, had bugs during contest :) )
this Educational Codeforces Round 111 problems are hard as compare to other Educational Codeforces Rounds.
Really Good C Problem
Problem C was a good one, learned a new concept through the problem in upsolving.
After reading the editorial of D, it doesn't seem even so hard!
There also exist solutions using segment trees and/or divide and conquer for C.
For the first solution, firstly find the next >= and <= element for each element. Now we need to find the closest element on the right which forms a non-increasing or a non-decreasing chain with the current element. If we do this, using a segment tree, we can do a two-pointers solution for greedily choosing the farthest possible end for a good subarray (for each index) using these values. To this end, the divide and conquer works as follows: break the array into two halves, and we will use the elements on the right as candidates for the middle elements for the chains of length 3, and update the closest values for the elements on the left. For achieving this, we can simply run coordinate compression and use prefix/suffix sums to compute the closest possible element which is at least (or at most) x. The time complexity is $$$O(n \log^2 n)$$$. Relevant submission: 122511482.
For the second solution (found by timreizin), we can do a much simpler sweep. For each element, we can use two segment trees (dynamic or with coordinate compression) and store the indices of the closest elements on the left, which are <= and >= the current value respectively. So if we query for the current element before updating it in the segment trees, we'll get at most 2 elements in the chain till just after those elements, and hence we can simply use the closer one to compute the largest subarray ending at the current index. The time complexity is $$$O(n \log n)$$$. Relevant submission: 122514591.
we can also find the number of bad subarrays and answer = total subarrays — bad subarrays
to find the number of bad subarrays we can find the left minimum, left maximum, right minimum and right maximum for every ith element, and from this, we can find the range of the bad subarrays by iterating on the array and taking the ith element as the middle element, and then through this range, we can find the number of the bad subarrays starting from the ith element. 122504943
Yes, exactly what I was trying to do in the contest, can you tell me how to find the second next >= and <= for each element in given array. I thought so hard on this, but still could not do it,any help would be appriciated. Therefore I stumbled on a different subproblem, which I mentioned here:https://codeforces.com/blog/entry/92810#comment-816475
I will show how I did it for a >= (<= is the same, with some easy changes). At first for every element find index of the nearest >= on the left. I needed a segment tree(dynamic or usual after compressing coordinates). In this segment tree we store -1 for all elements at the beginning. Then, we will work with our array from 0 to n — 1. After proceeding each index I set value at point a[I] in a segtree to it's "index of the nearest >= on the left". For index i(when we proceed them from 0 to n — 1, in the same cycle with updates to segtree) I take maximum in a range(a[I], maxA). Result of this query will be the needed index.I think this submission will help in understanding. 122484928
The key idea in the first solution is to essentially look at the second element of each chain (which has 3 elements each). And this is what I do in the divide and conquer stage. Basically, you look at all possible chains with the middle element in the right half, and the first element in the left half. All the rest have the first two elements in the same half, and this case is covered by the two recursive calls to the left and the right halves.
In problem C, why we can't form a bad triple when i<j<k isn't true?
Because we can — so statement "we can't" is false. It's really obvious — draw them (all 6 variation of < and > for second coords) — it's really easier to see than to write ~10-15 lines of words explaining this variations.
We can if k < j < i, but j needs to be between i and k.
Consider, for example:
i < k < j
Then:
d(p, r) = |k - i| + |ak - ai| = k - i + |ak - ai|
d(p, q) + d(q,r) = |j - i| + |aj - ai| + |k - j| + |ak - aj| = j - i + j - k + |aj - ai| + |ak - aj|
But:
|aj - ai| + |ak - aj| >= |ak - ai|
and, since j > k
j - i + j - k > k - i + k - k = k - i
so
d(p, q) + d(q,r) > k - i + |ak - ai| = d(p, r)
So there can be no bad triple if i < k < j
Similarly there can be no bad triple for j < i < k, k < i < j, or j < k < i
because coordinate of x is i,j,k。if one array is good.These three points is in the same straight line
Sorry,it's bad triple not good and they are not must in the same straight.if i<j<k ,(i,k)=hk-hi+k-i;(i,j)= hj-hi+j-i,(j,k)=hk-hj+k-j;(i,j)+(j,k)=hk-hj+hj-hi+k-j+j-i=hk-hi+k-i=(i,k)
Video Editorials of this Round A. Find The Array B. Maximum Cost Deletion
I loved Problem C !
ABC-forces
I have a doubt in problem A
I figured out the solution is ceil(sqrt(n)) pretty fast but was afraid should I submit it or not.
The reason is I faced penalty for using ceil function to round up divided answers. I learnt I should write (a+b-1)/b instead of ceil(a/b) because ceil function has precision errors.
But when I submitted ceil(sqrt(n)), it passed. So, why isn't it showing precision error in that case?
Is the test cases weak, or is there something about ceil function I'm missing ?
ceilfunction inC++will print the number as it's if the number < $$$10^6$$$ otherwise it'll print it in the form1e+n(like $$$10^6$$$ it'll printed as 1e+06) but in A the maximum number will be printed is 71 so doubles will workPS: that's will not change that
(a + b - 1) / bis always better, so try as possible to avoid doubles!I didn't get the equations for the solution of problem A. Specially these lines - "Let ⌈s√⌉=d. By taking 1+3+5+7+⋯+2d−3, we achieve a sum of (d−1)2 using d−1 elements. s−(d−1)2 is not less than 1 and not greater than 2d−1 (since (d−1)2−−−−−−−√=d−1, and (d−1)2+2d−−−−−−−−−−−√>d). Thus, we can just add s−(d−1)2 to our array, and the sum becomes exactly s."
Would you please explain little more or any reference to understand these lines.
Basically if sum is n*n then it answer is n, if sum is less than that of n*n but more than (n-1)*(n-1) the answer is still n as:
suppose sum is 9 => array is 1 3 5`suppose sum is not 9 but between 4 and 9 (say 8) => then array is 1 3 4`suppose it is 7 => then array is 1 2 4Similarly we can prove that we can make changes to array so that array becomes equal to sum but with same number of elements.
Problem C was actually nice. Actually there is a kinda interesting theorem, that might help in such problems: for every sequence numbers length N the product of the length of LIS(longest increasing subsequence) and LDS(longest decreasing subsequence) is greater than N. For instance, either length of LIS or LDS should be greater than ceil(sqrt(N)).
So if we take a sequence of length 4, that max(length(LIS), length(LDS)) is 2, because sqrt(4) is 2 and this is an integer. But, for length 5, there always would a LIS or LDS of length 3. This is exactly what we had to observe in this particular problem. Hope this little fact might help you in the future
P.S. on russian ITMO-wiki there is a proof of this theorem
https://en.wikipedia.org/wiki/Erd%C5%91s%E2%80%93Szekeres_theorem
English page for the same theorem
https://mathworld.wolfram.com/Erdos-SzekeresTheorem.html
thanks a lot!
Solution for A problem without a loop:
Is it a bad solution or is it considered bad to publish your own solutions? I don't get it, I am new here.
You have several dropdown options before you comment. The rightmost one is a CF symbol. Click on spoilers and then post your code. Like this
def beautiful_array(num): square_root = math.sqrt(num) if square_root.is_integer(): return int(square_root) else: return int(math.floor(square_root) + 1)As to how to format your code inside the spoiler(or in general). look here
Or you could post the link to your code.
In problem C Manhattan Subarrays
Why does a sequence of length greater than or equal to 5 have a subsequence of length 3 that does not increase or decrease
How long must a sequence contain a non-decreasing subsequence of length 4 or a non-increasing subsequence of length 4? Is there any pattern?
10, look at Erdős–Szekeres theorem.
I can't make any sense of the code used to calculate pos[i][j] in problem E
I have a simpler implementation imo .you can check it out, to calculate pos[i][j] you iterate backwards while keeping a counter (called cur in the code) for each alphabet meaning what is the longest substring with all letters equal to this alphabet starting from the current position 122726559
It represents the minimum position which is free after we have placed a block of length "mid" (from the binary search) after the index i for some particular letter j.
Now there are two cases---->
Either from i to i + mid there is not a single letter of type other than j or '?'. In this case we can place a block here so update pos[ i][ j] to i+d . To ensure this we move Check once from 0 to i-1 and the next time from (length of array)-1 to i+1.
We have some guy other than our letter j and '?'. Update it to pos[ i+1][ j]
Regarding Problem C: "The final observation is that any sequence of length at least 5 contains either non-decreasing or non-increasing subsequence of length 3" I think the array 5 8 3 4 2 doesn't contain any sub-array of length 3 which is either non-increasing or non-decreasing. All the sub-arrays of length 3: 5 8 3, 8 3 4 and 3 4 2 are neither non-increasing nor non-decreasing. Problem stated "A subarray of the array a is the array a(l),a(l+1),…,ar for some 1≤l≤r≤n" Am I missing something?
I guess, it's a confusion about terminology. The problem statement explains what it means by "good array" and what it means by "subarray". The editorial uses a new word "subsequence", which is not the same as "subarray".
Your array [5, 8, 3, 4, 2] is not good, because we can choose three distinct indices $$$i=2$$$, $$$j=3$$$, $$$k=5$$$. Points $$$(8, 2)$$$, $$$(3, 3)$$$ and $$$(2, 5)$$$ form a bad triple.
Yes you are right. I didn't notice it.
Can someone please explain to me the solution of Problem B, especially this part —
cout << n * a + max(n * b, (m / 2 + 1) * b) << '\n';You have to delete all the characters in the whole string so the number of points you receive first is a*n. Therefore, you will consider 2 cases:
Case 1 is b >= 0: you have to maximize the operations (because the more operations you do, the more number of points you will get because b >= 0) so the answer of this case will be n * b.
Case 2 is b < 0: you have to minimize the operations (because the more operations you do, the less number of points you will get because b < 0).
I have an example: 10000111100011111.
You see that the string above has 5 blocks, 2 blocks adjacent has no equal characters and the string consists of just 1s and 0s. You will find out that, instead of delete 5 blocks in 5 operations (1 -> 000 -> 1111 -> 000 -> 11111), we just need to delete the middle blocks (*), the blocks that adjacent to this block will merge into one so that it takes 3 operations (0000 -> 000 -> 1111111111), which is less than 5 operations. If the string has m blocks 0s and 1s, the number of operations (*) is m/2 and 1 operation more to delete the rest characters. Therefore, the answer of this case is m/2 + 1.
Because you need to find the optimal result of the problem, you will compare m/2 + 1 to n*b to find what is larger, after that plus n*a and print the result.
(Sorry for my bad english :( hope you will understand.)
I drew a picture to show that
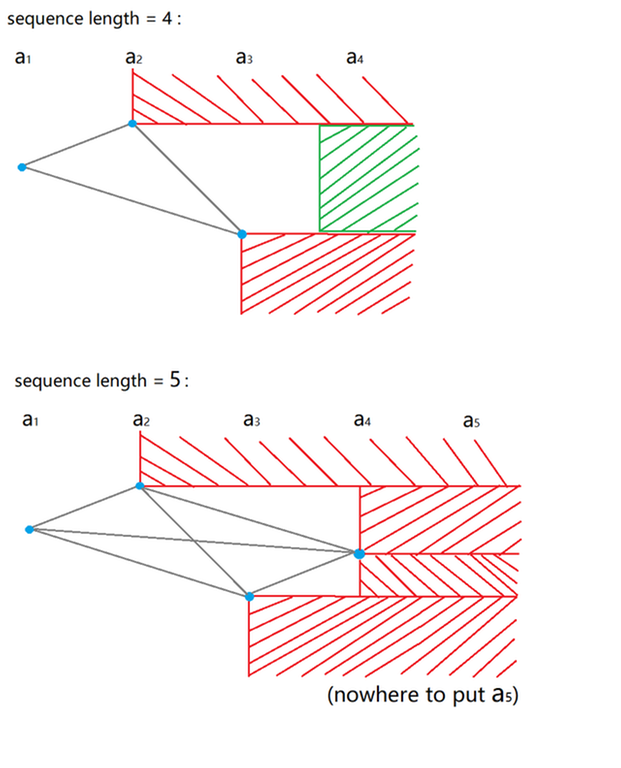
any sequence of length at least 5 contains either non-decreasing or non-increasing subsequence of length 3in problem C. I hope it helps.blue point -> value of a[i]
grey line -> possible combination of a[i] and a[j]
red area -> the last number cannot be placed here (otherwise there is bad subsequence)
green area -> the last number can be placed here
I can present a more sound proof for C that doesn't use any theorem. First we can prove that for any pair $$$a_1, a_2, a_3$$$, $$$a_1 <= a_2 <= a_3$$$ and $$$a_1 >= a_2 >= a_3$$$ are forbidden because they will result in a bad tripe.
Now after that, for any five consecutive numbers the only "valid" constructions will be $$$a_1 <= a_2 >= a_3 <= a_4 >= a_5$$$ and $$$a_1 >= a_2 <= a_3 >= a_4 <= a_5$$$. I will show that these are not "valid".
In the first case: $$$a_1 <= a_2 >= a_3 <= a_4 >= a_5$$$ Let's observe $$$a_2$$$ and $$$a_4$$$: if $$$a_2 <= a_4$$$, then $$$a_1, a_2, a_4$$$ will be a bad triple, otherwise if $$$a_2 >= a_4$$$, $$$a_2, a_4, a_5$$$ will be a bad triple.
The second case can be proved analogically.
This way we proved that a good subarray will have length smaller or equal to 4.
Most easiest prove, thanks bro
First time seeing Boruvka's Algorithm in use. Nice problems! Especially E and F