Introduction
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case of the general Boolean satisfiability problem, which can involve constraints on more than two variables, and of constraint satisfaction problems, which can allow more than two choices for the value of each variable. But in contrast to those more general problems, which are NP-complete, 2-satisfiability can be solved in polynomial time. -Wikipedia
If you have not heard of propositional logic before, plead read about it here. Wikipedia links have been provided wherever a term has been used for the first time in this tutorial. The whole algorithm is based on graph theory so it will help to be familiar with directed graphs and strongly connected components beforehand.
By representing our formula in the 2-Conjunctive Normal Form, we can find an assignment of values for our variables in $$$O(N + M)$$$ where we have $$$N$$$ variables and $$$M$$$ clauses or report that the proposition isn't satisfiable. Simply put, a formula in the 2-CNF is an AND of ORs where each clause contains exactly two literals.
Thanks to Monogon for providing valuable suggestions and helping with the proof.
A Few Definitions
$$$\lnot x$$$ is the complement of $$$x$$$. If $$$x$$$ is $$$\it{true}$$$, $$$\lnot x$$$ is $$$\it{false}$$$. If $$$x$$$ is $$$\it{false}$$$, $$$\lnot x$$$ is $$$\it{true}$$$.
$$$(x \lor y)$$$ stands for $$$x$$$ OR $$$y$$$ (disjunction). It results in $$$\it{true}$$$ only if at least one of $$$x$$$ and $$$y$$$ is $$$\it{true}$$$.
$$$(x \land y)$$$ stands for $$$x$$$ AND $$$y$$$ (conjunction). It results in $$$\it{true}$$$ only if $$$x$$$ and $$$y$$$ are both assigned $$$\it{true}$$$.
$$$(x \Rightarrow y)$$$ stands for $$$x$$$ implies $$$y$$$ (implication). In order for it to result in $$$\it{true}$$$, if $$$x$$$ is $$$\it{true}$$$, $$$y$$$ has to be $$$\it{true}$$$. Otherwise, $$$y$$$ could be $$$\it{true}$$$ or $$$\it{false}$$$.
$$$(x \iff y)$$$ stands for ($$$x$$$ implies $$$y$$$) AND ($$$y$$$ implies $$$x$$$). It results in $$$\it{true}$$$ only if both $$$x$$$ and $$$y$$$ have the same value.
2-CNF consists of a bunch of OR clauses combined with AND. Each OR clause must result in $$$\it{true}$$$ for a proposition to be satisfied.
Main Idea
We want to create a directed graph of implications where each node is a variable.
Let's consider a disjunction of two literals $$$x$$$ and $$$y$$$ to see what all information we can deduce from it. We know that: $$$(x \lor y) \iff (\lnot x \Rightarrow y)$$$ (Implication Law).
This becomes an edge $$$(\lnot x, y)$$$ in our graph. An edge $$$(u, v)$$$ in this tutorial is directed from $$$u$$$ to $$$v$$$.
We must also add an edge $$$(\lnot y, x)$$$ to our graph.
Since our formula is a conjunction of clauses of the form $$$(x \lor y)$$$, we will be adding edges of this type only.
Do keep in mind that if there exists an edge $$$(x, y)$$$ in the graph, there also exists an edge $$$(\lnot y, \lnot x)$$$.
The Algorithm
Here is what the graph looks like for the following proposition in 2-CNF:
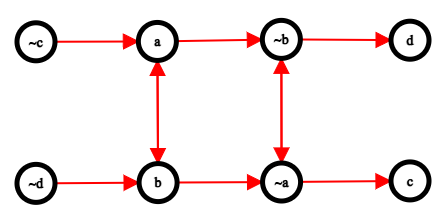
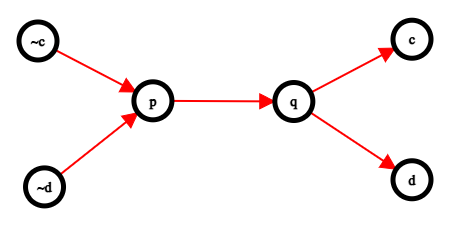
Shown above is the implication graph and its condensation graph.
After we have added all the required edges, we want to find all the strongly connected components in the graph. The condensation graph is acyclic (graph obtained on compressing each SCC into a single node but retaining connections). Visualise this as a graph where SCCs are connected to each other with edges directed from left to right (as shown in the diagrams above).
What happens when for any variable $$$x$$$, $$$\lnot x$$$ lies in the same SCC as $$$x$$$? There is no valid assignment of truth values. Setting $$$x$$$ to $$$true$$$ would imply that $$$\lnot x$$$ has to be $$$true$$$ and setting $$$\lnot x$$$ to $$$true$$$ would imply that $$$x$$$ has to be $$$true$$$. In both cases, this leads to a contradiction. Hence, no answer exists.
When that is not the case, we can assign values to all variables.
Let $$$id[v]$$$ represent the index of the SCC (in any valid topological ordering) that contains $$$v$$$. In the topological ordering, for any two nodes $$$u$$$ and $$$v$$$, if $$$id[u]$$$ < $$$id[v]$$$, the SCC containing $$$u$$$ lies to the left of the SCC containing $$$v$$$. If they are equal, both nodes lie in the same SCC. If it's the opposite, $$$u$$$'s SCC lies to the right of $$$v$$$'s SCC.
For each variable $$$x$$$:
1. If $$$id[x]$$$ > $$$id[\lnot x]$$$, let's set $$$x$$$ to $$$\it{true}$$$ and $$$\lnot x$$$ to $$$\it{false}$$$.
2. If $$$id[x]$$$ < $$$id[\lnot x]$$$, let's set $$$x$$$ to $$$\it{false}$$$ and $$$\lnot x$$$ to $$$\it{true}$$$.
An important observation is that all variables in a SCC have the same truth value.
This way, we can satisfy our proposition in linear time.
Why Does It Work?
The implication graph is set up in a way that our proposition is satisfied if we don't have a case where some node $$$u$$$ which has been assigned $$$true$$$ can reach some node $$$v$$$ which has been assigned $$$false$$$.
If some variable $$$x$$$ is assigned true, we know that $$$id[x]$$$ > $$$id[\lnot x]$$$ because of how we construct the answer. Keep in mind that if $$$x$$$ can reach $$$y$$$, $$$\lnot y$$$ can reach $$$\lnot x$$$ in our implication graph.
Let's prove that we don't have two nodes $$$u$$$ and $$$v$$$ such that there is a path from $$$u$$$ to $$$v$$$ and $$$u$$$ is assigned $$$true$$$ while $$$v$$$ is assigned $$$false$$$. Assume that this is the case. What does this mean? $$$id[\lnot u] < id[u]$$$ because $$$u$$$ has been assigned $$$true$$$ and $$$id[v] < id[\lnot v]$$$ because $$$v$$$ has been assigned $$$false$$$. According to our assumption, $$$id[\lnot u] < id[u] \leq id[v] < id[\lnot v]$$$. However, since there exists a path from $$$u$$$ to $$$v$$$, there has to exist a path from $$$\lnot v$$$ to $$$\lnot u$$$. That would imply that $$$id[\lnot u] \ge id[\lnot v]$$$. This contradicts our previous inequality.
Types of Constraints
Keep in mind that:
1. Forcing a variable to be $$$true$$$
If we want to force $$$x$$$ to be true, it is equivalent to adding a clause $$$(x \lor x)$$$.
2. Exactly one variable must be $$$true$$$
This is equivalent to $$$(x \lor y) \land (\lnot x \lor \lnot y)$$$.
3. At least one variable must be $$$true$$$
This is just a clause $$$(x \lor y)$$$.
4. Both variables must have the same value
This is equivalent to $$$(\lnot x \lor y) \land (x \lor \lnot y)$$$.
Implementation
After we figure out the clauses that need to be added and set up the graph adjacency list, we need to extract all strongly connected components (using any algorithm keeping in mind its efficiency). Kosaraju's algorithm or Tarjan's algorithm is commonly used to extract strongly connected components. I use Kosaraju's algorithm in my implementation below. We want to give each SCC an ID and store for each node which SCC it belongs to. Variables can be numbered from $$$1$$$ to $$$N$$$ and their complements can be numbered from $$$N + 1$$$ to $$$2N$$$. So $$$i + N$$$ is $$$i$$$'s complement.
CSES — Giant Pizza
Try to solve this problem on your own.
Flipping Cards
Though this problem asks only whether it is possible to place the cards in such a way that no two cards are showing the same picture, try to find a valid arrangement as well.











Arujorz
great post!
One more beautiful Problem.
thank's for the blog arujbansal
Great work !!! , You can add one more idea here "AtMostOne" , see this problem and solution by ksun --> here
do you miss add_clause_xor(i, f, j, !g); in void add_clause_and(int i, bool f, int j, bool g);
thanks for the proof.
one more problem here