Этот раунд был подготовлен разработчиками Яндекса.
Problem А. НольОдин
Для решения задачи сначала переведём строки в двоичные числа, а после сравним их. Поскольку из условия ясно, что числа могут получиться порядка $$$2^{333}$$$, сравнивать их будем без перевода в числовой тип данных.
Problem B. Плитки 2x2
Для решения введем классы эквивалентности (совпадения) плиток $$$2 \times 2$$$. Если плиток каждого класса в наборе будет не менее требуемого числа для картинки, то ответ будет положительный.
Для определения класса эквивалентности можно выбрать главного представителя класса. В случае с матрицей $$$2 \times 2$$$ подойдет минимальный кортеж из всех четырех поворотов матрицы.
Problem C. Шары и коробки
Пусть $$$sumA = \sum_{i = 1}^k a_i$$$. Давайте научимся проверять, может ли некоторое число коробок $$$x, 1 \le x \le sumA$$$ удовлетворять всем условиям. Для этого должно выполняться следующее:
- $$$x$$$ является делителем $$$sumA$$$
- $$$a_i - x \cdot b_i \ge 0$$$ для любого цвета $$$i$$$
Таким образом, мы можем перебрать делители числа $$$sumA$$$ и для каждого проверить выполнение второго условия, а среди всех таких $$$x$$$, что условие выполняется, выбрать максимальный.
При выводе ответа нужно аккуратно рассмотреть случай $$$b_i = 0$$$.
Problem D. Матрица
Для удобства будем использовать следующие обозначения $$$n=2^{n'}$$$, $$$m=2^{m'}$$$.
- Рассмотрим случай $$$n=m,\,n>1$$$. После первого шага матрица будет иметь следующий вид:

После второго шага матрица будет иметь следующий вид: 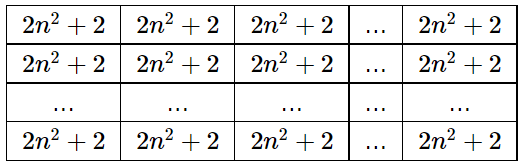
Таким образом, после второго шага и до самого конца вся матрица будет заполнена одинаковыми числами.
Имеем, что суммарно различных чисел будет выписано $$$n^{2}+\frac{n}{2}+\log_2{\frac{n^2}{2}}$$$ ($$$1$$$, $$$2$$$, ..., $$$n^2$$$, $$$n^2+2$$$, $$$n^2+4$$$, ..., $$$n^2+n$$$, $$$2(n^2+1)$$$, $$$2^2(n^2+1)$$$, ..., $$$\frac{n^2(2n^2+1)}{2}$$$.
- Рассмотрим случай $$$n<m$$$. После первого шага матрица будет иметь следующий вид:

После $$$i$$$-го из следующих ($$$m'-n'-1$$$) шагов матрица будет иметь следующий вид: 
Обратим внимание, что в этих матрицах все числа более $$$nm$$$ встречаются только однажды (занимают целую строку одной из матриц). На следующем шаге и до самого конца вся матрица будет заполнена одинаковыми числами.
В отличие от первого случая мы можем рассмотреть каждую из $$$n$$$ строк матрицы отдельно ($$$n < 2^{15}$$$).
- Рассмотрим случай $$$n>m$$$. После первого шага матрица будет иметь следующий вид:

После $$$i$$$-го из следующих ($$$n'-m'$$$) шагов матрица будет иметь следующий вид: 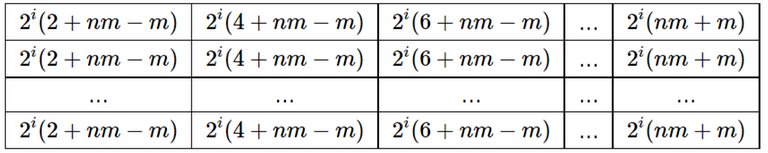
Следует отметить, что максимальный элемент матрицы на шаге $$$i$$$ меньше минимального элемента матрицы на шаге $$$i+1$$$.
Имеем, что суммарно различных чисел будет выписано $$$nm+\frac{m}{2}+m\log_2{\frac{n}{m}}+\log_2{\frac{m^2}{2}}$$$.
Problem E. Сортировка матрицы
Рассмотрим множество нулей в отсортированной матрице. Тогда количество операций, это количество единиц первоначальной матрицы, которые лежат в этом множестве. Множество нулей образует диаграмму Юнга — в каждой строке множество клеток образует отрезок прижатый к левому краю и каждая последующая строка содержит меньше или столько же клеток множества. Поэтому нам нужно построить диаграмму Юнга заданного размера, которая содержит как можно меньше единиц.
Будем решать задачу динамическим программированием. Для каждой клетки матрицы рассмотрим прямоугольник с углами в этой клетке и в правом верхнем угле матрицы. Для каждого размера диаграммы Юнга внутри этого прямоугольника, посчитаем минимальное число единиц, которое в ней может содержаться. Клеток матрицы $$$O(nm)$$$ и размеров диаграммы Юнга $$$O(nm)$$$, поэтому нам надо посчитать ответы для $$$O((nm)^2)$$$ подзадач.
Покажем как подсчитать ответ в каждой из подзадач. Рассмотрим клетку в нижнем левом угле прямоугольника, в котором мы рассматриваем диаграмму Юнга. Она либо принадлежит диаграмме, либо нет.
Если она принадлежит диаграмме, то все клетки выше нее тоже принадлежат диаграмме Юнга. В таком случае мы свели задачу к прямоугольнику, у которого нижний левый угол на одну клетку правее, а размер диаграммы Юнга меньше на размер столбца. Чтобы посчитать сколько единиц этот столбец добавил к ответу, предпросчитаем для каждой клетки матрицы количество единиц нестрого выше нее в этом же столбце. Этот предпросчет можно сделать за $$$O(nm)$$$, идя сверху вниз.
Во втором случае, клетка в нижнем левом угле не принадлежит диаграмме. В таком случае мы свели задачу к прямоугольнику, у которого нижний левый угол на одну клетку выше. Ни размер диаграммы Юнга, ни ответ при этом не изменяются.
Остается взять минимум из этих двух случаев. Поскольку каждый случай можно рассмотреть за $$$O(1)$$$ времени, то всего нужно $$$O((nm)^2)$$$ действий. Состояния динамики можно рассчитывать сверху вниз и справа налево. Кроме того, можно хранить лишь текущую и следующую строку или столбец динамики. Это позволяет использовать лишь $$$O(\min(n^2m,nm^2))$$$ памяти.
Problem F. Переворот пути
$$$O(n^2)$$$ решение
Чтобы решить задачу за время $$$O(n^2)$$$, достаточно перебрать все пары $$$(p, q)$$$ и для каждой из них найти ответ за $$$O(1)$$$. В этом решении потребуется находить расстояние между любой парой вершин за $$$O(1)$$$. Для этого можно выполнить поиск в глубину или в ширину из каждой вершины, таким образом получим величины $$$d_{ij}$$$ — расстояние между вершинами $$$i$$$ и $$$j$$$.
Если $$$p$$$ и $$$q$$$ зафиксированы, то любая вершина $$$x$$$ находится в одном из следующих четырех состояний:
- $$$x$$$ лежит на пути между $$$p$$$ и $$$q$$$ включительно. В этом случае выполняется условие: $$$d_{px} + d_{xq} = d_{pq}$$$.
- $$$x$$$ лежит в части дерева за вершиной $$$p$$$ — $$$d_{xp} + d_{pq} = d_{xq}$$$.
- $$$x$$$ лежит в части дерева за вершиной $$$q$$$ — $$$d_{pq} + d_{qx} = d_{px}$$$.
- $$$x$$$ лежит на ответвлении на пути $$$p-q$$$. В этом случае, если все три условия выше ложные.
Рассмотрим варианты расположения вершин $$$1$$$ и $$$n$$$ относительно $$$p$$$ и $$$q$$$? Всего может быть 16 вариантов: $$$1$$$/$$$n$$$ (независимо) может иметь одно из описанных выше расположений (выбор из 4). Расстояние между $$$1$$$ и $$$n$$$ изменится только в следующих случаях (8 из 16):
- $$$1$$$ за вершиной $$$p$$$, $$$n$$$ на самом пути или на ответвлении от пути $$$p-q$$$.
- $$$1$$$ за вершиной $$$q$$$, $$$n$$$ на самом пути или на ответвлении от пути $$$p-q$$$.
- $$$n$$$ за вершиной $$$p$$$, $$$1$$$ на самом пути или на ответвлении от пути $$$p-q$$$.
- $$$n$$$ за вершиной $$$q$$$, $$$1$$$ на самом пути или на ответвлении от пути $$$p-q$$$.
Так как эти случаи идентичны, рассмотрим только первый из них. Итак, $$$1$$$ за вершиной $$$p$$$ и $$$n$$$ на пути или ответвлении от пути $$$p-q$$$. Перед разворотом расстояние равно $$$d_{1p} + d_{pn}$$$, а после разворота становится $$$d_{1p} + d_{qn}$$$. Подзадача на 2 балла решена.
Решение для цепочки
В этой подзадаче дерево вытянуто в цепочку. Разберем решение за $$$O(n)$$$. Расстояние изменяется только в том случае, если одна из вершин $$$p$$$ и $$$q$$$ расположена за пределами пути $$$1-n$$$, а вторая — внутри этого пути.
Сперва вычислим расстояние между $$$1$$$ и $$$n$$$ и умножим его на $$$\frac{n(n-1)}{2}$$$. Определим, как изменяется ответ после каждой операции разворота, не вычисляя его каждый раз в явном виде.
Будем считать, что $$$1$$$ расположена слева от $$$n$$$, обозначим количество вершин слева от $$$1$$$ через $$$a$$$, а количество вершин строго между $$$1$$$ и $$$n$$$ — через $$$b$$$.
.... (a slots) .... [1] .... (b slots) .... [N] ....
Пусть $$$d$$$ величина, на которую изменяется расстояние между вершинами после разворота. Если $$$p$$$ занимает одно из $$$a$$$ положений слева от $$$1$$$, сколько есть походящих положений для $$$q$$$ на пути $$$1-n$$$ для фиксированного значения $$$d$$$? Рассмотрим иллюстрации для $$$d=1$$$ и $$$d=2$$$:
$$$d = 1$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [ ] [p] [q] [ ] [ ] [ ] [ ] [ ] [N] [ ] [ ]
[ ] [ ] [ ] [ ] [p] [ ] [1] [q] [ ] [ ] [ ] [ ] [N] [ ] [ ]
[ ] [ ] [ ] [p] [ ] [ ] [1] [ ] [q] [ ] [ ] [ ] [N] [ ] [ ]
...
$$$d = 2$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [p] [ ] [q] [ ] [ ] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [p] [ ] [ ] [1] [q] [ ] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [p] [ ] [ ] [ ] [1] [ ] [q] [ ] [ ] [N] [ ] [ ] [ ]
...
Проанализировав эти случаи имеем. Для фиксированного $$$d$$$ ответ на вопрос выше $$$\min(a - d + 1, b + 1)$$$ (определяем, какой из участков закончится раньше). Поэтому к ответу следует прибавить $$$d \cdot \min(a - d + 1, b + 1)$$$.
Изменение длины может быть и отрицательным (расстояние между $$$1$$$ и $$$n$$$ уменьшится). Рассмотрим иллюстрации:
$$$d = 1$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [ ] [ ] [q] [p] [ ] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [ ] [q] [1] [ ] [p] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [q] [ ] [1] [ ] [ ] [p] [ ] [N] [ ] [ ] [ ]
...
$$$d = 2$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [ ] [ ] [q] [ ] [p] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [ ] [q] [1] [ ] [ ] [p] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [q] [ ] [1] [ ] [ ] [ ] [p] [N] [ ] [ ] [ ]
...
Количество подходящих под $$$d$$$ пар вершин равно $$$\min(b - d + 1, a + 1)$$$.
Положительные $$$d$$$ изменяются от $$$1$$$ до $$$a$$$, отрицательные $$$d$$$ изменяются $$$1$$$ до $$$b$$$ (по модулю). Для каждого значения $$$d$$$ находим изменение ответа за $$$O(1)$$$.
Бонус: зная $$$a$$$ и $$$b$$$, можно без итерирования по $$$d$$$ (из-за чего решение становится $$$O(n)$$$) вычислить ответ за $$$O(1)$$$. Сможете вывести нужную формулу?
Решение в общем случае
В решении за $$$O(n^2)$$$ мы разделили вершины на четыре класса в зависимости от расположения относительно $$$p$$$ и $$$q$$$. В общем случае также потребуется подобный подход, но относительно вершин $$$1$$$ и $$$n$$$.
Пусть величина $$$d_{1x}$$$ равна расстоянию от $$$x$$$ до $$$1$$$, а $$$d_{nx}$$$ — от $$$x$$$ до $$$n$$$. Пусть $$$m$$$ это расстояние между вершинами $$$1$$$ и $$$n$$$. Тогда вершины могут быть:
- за вершиной $$$1$$$ или сама вершина $$$1$$$: $$$d_{1x} + m = d_{nx}$$$,
- за вершиной $$$n$$$ или сама вершина $$$n$$$: $$$d_{1x} = m + d_{nx}$$$,
- строго на пути $$$1-n$$$: $$$d_{1x} + d_{nx} = m$$$, $$$x \ne 1$$$ и $$$x \ne n$$$,
- на ответвлении пути, если все условия выше ложные.
Расстояние изменяется в двух случаях:
- $$$p$$$ строго между $$$1$$$ и $$$n$$$ или одна из них, $$$q$$$ за вершиной $$$1$$$ или вершиной $$$n$$$,
- $$$p$$$ строго между $$$1$$$ и $$$n$$$, $$$q$$$ лежит на ответвлении, и корень ответвления $$$z$$$ лежит строго между $$$1$$$ и $$$n$$$ и $$$p \ne z$$$.
Первый случай:
Переберем значение $$$q$$$. Если вершина $$$q$$$ зафиксирована, как изменится ответ?
... [Q] ..... (a slots) ... [1] ... (b slots, P is somewhere on [1, N)) ... [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [ ] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [ ] [ ] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [N] ...
Для первой строки иллюстрации ($$$p=1$$$) изменение равно $$$a$$$ (т.е. расстоянию $$$d_{1q})$$$, для второй строки — $$$a-1$$$, и т.д. Когда $$$n$$$ и $$$p$$$ смежные вершины, изменение равно $$$a-b$$$ (отрицательное при $$$a < b$$$). Общее изменение ответа равно сумме последовательных чисел от $$$a$$$ до $$$a - b$$$, может быть вычислено за $$$O(1)$$$.
Если правильно решить этот случай, то будет покрыта группа с линейным деревом.
Второй случай:
Вновь переберем значение $$$q$$$. Зная $$$d_{1q}$$$ и $$$d_{nq}$$$, можно найти корень ответвления $$$z$$$ (т.к. мы можем вычислить длину ответвления $$$\frac{d_{1q} + d_{nq} - m}{2}$$$, где $$$m$$$ это расстояние между $$$1$$$ и $$$n$$$, $$$m = d_{1n}$$$) и величины $$$d_{1z}$$$ и $$$d_{nz}$$$.
У нас вновь два аналогичных случая (выбор между $$$1$$$ и $$$n$$$), рассмотрим один из них.
...
[N]
[ ]
...
[ ]
... [1] ... (a slots, P is somewhere on (1, Z)) ... [Z] ... (b slots) ..... [Q] ...
... [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
... [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [ ] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
... [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [ ] [ ] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
...
... [1] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
Здесь $$$a = d_{1z} - 1$$$, $$$b$$$ длина ответвления уменьшенная на 1. Как видно из иллюстрации, ответ изменяется, когда $$$p$$$ перемещается от $$$1$$$ к $$$z$$$, не включая $$$1$$$ и $$$z$$$. Вновь потребуется сумма арифметической прогрессии: $$$b + (b-1) + \ldots + (b-a+1)$$$, которую можем вычислить за $$$O(1)$$$.
Таким образом, в обоих случаях итерируемся по вершине $$$q$$$, для каждого выбора $$$q$$$ находим изменение ответа за $$$O(1)$$$, что дает общую трудоемкость $$$O(n)$$$.











A small note about the Python solution on D. In Python you don't need to use floats for
instead you can (and probably should) use
int.bit_lengthThis is not just a Python trick. C++20 introduces the function
bit_widthwhich is the same thing as Python'sbit_length.