Problemset was prepared by Yandex employees.
Problem А. ZeroOne
Firstly, let's convert input strings into two binary strings. Because the numbers can be approximately $$$2^{333}$$$ we shouldn't convert them into the numeric type and should compare their string representations
Problem B. Tiles 2x2
To solve to problem we can introduce equivalence classes of tiles $$$2 \times 2$$$. If the number of tiles of each class in the set is not less than the required number for the picture, the result will be positive.
To determine the equivalence class one can choose the main representative of the class. In the case of the matrix $$$2\times 2$$$ the minimum tuple of all four rotations of the matrix is suitable.
Problem C. Balls and Boxes
Let $$$sumA = \sum_{i = 1}^k a_i$$$. To check whether a certain number of boxes $$$x, 1\le x\le sumA,$$$ satisfies all conditions the following must be fulfilled:
- x is a divisor of $$$sumA$$$
- $$$a_i - x \cdot b_i \ge 0$$$ for each color $$$i$$$
So, we can iterate over the divisors of the number $$$sumA$$$, check the fulfillment of the second condition, and choose the maximum $$$x$$$ that the condition is met.
The tricky part of the problem is to print the result. One should be attentive with the case $$$b_i=0$$$.
Problem D. Matrix
For convenience, we will use the following notation $$$n=2^{n'}$$$, $$$m=2^{m'}$$$.
- Let's consider the case $$$n=m,\,n>1$$$. After the first step the matrix has the following form:

After the second step the matrix has the following form: 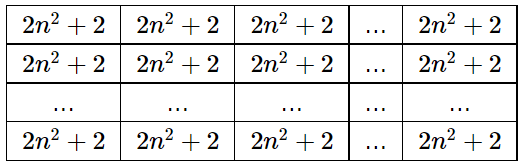
Thus, after the second step and until the very end, the entire matrix is filled with the same numbers.
Summarizing this information, the total of different numbers will be written out is $$$n^{2}+\frac{n}{2}+\log_2{\frac{n^2}{2}}$$$ ($$$1$$$, $$$2$$$, ..., $$$n^2$$$, $$$n^2+2$$$, $$$n^2+4$$$, ..., $$$n^2+n$$$, $$$2(n^2+1)$$$, $$$2^2(n^2+1)$$$, ..., $$$\frac{n^2(2n^2+1)}{2}$$$.
- Let's consider the case $$$n<m$$$. After the first step the matrix has the following form:

After the $$$i_{th}$$$ of following ($$$m'-n'-1$$$) steps the matrix has the following form: 
Note that in these matrices any number over $$$nm$$$ occurs only once (an entire row of one of the matrices). At the next step and until the very end, the entire matrix is filled with the same numbers.
Unlike the first case, we can consider each of the $$$n$$$ rows of the matrix separately ($$$n < 2^{15}$$$).
- Let's consider the case $$$n>m$$$. After the first step the matrix has the following form:

After the $$$i_{th}$$$ of following ($$$n'-m'$$$) steps the matrix has the following form: 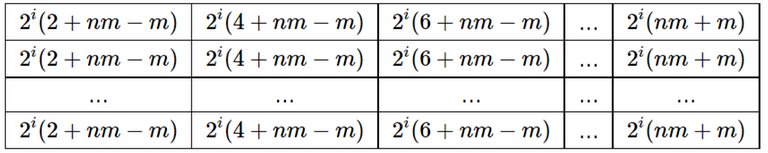
It should be noted that the maximum element of the matrix at step $$$i$$$ is less than the minimum element of the matrix at step $$$i+1$$$.
Summarizing this information, there are $$$nm+\frac{m}{2}+m\log_2{\frac{n}{m}}+\log_2{\frac{m^2}{2}}$$$ different numbers will be written out .
Problem E. Matrix sort
Let us consider the set of zeros in the sorted matrix. The number of operations is the number of ones in the original matrix inside this set. The set of zeros forms a Young tableau which is the set of cells, such that in each row and column zeroes form a prefix. So we need to construct Young tableau of the given size which contains the least amount of ones in the original matrix.
We are going to solve the problem with dynamic programming. For each cell of the matrix we consider the rectangle with one corner in this cell and the opposite corner in the right upper corner of the matrix. For each possible size of Young tableau inside this rectangle we calculate the least number of ones it can contain. There are $$$O(nm)$$$ cells in the matrix and $$$O(nm)$$$ sizes of Young tableau so we need to solve $$$O((nm)^2)$$$ subproblems.
Let us show how to solve each subproblem. Let us consider the cell in the left lower corner of the rectangle where we consider our Young tableaus. It is either belongs to the Young tableau(meaning that it will contain zero in the end) or not.
If it belongs to the Young tableau, then all cells above it belong to the Young tableau too. In this case we reduced our problem to the rectangle with left lower corner one cell to the right from our cell and Young tableau size is reduced by the size of the column. In order to calculate how many ones we got inside the column, we precalculate for each cell of the matrix the number of ones non-strictly above it in the same column. This precalculation can be made in $$$O(nm)$$$, if we go from top to bottom.
In the second case, the left lower corner does not belong to the Young tableau. In this case we reduced our problem to the rectangle with left lower corner one cell above from our cell and Young tableau size as well as the answer remained unchanged.
All what is left, is to take the minimum of these two cases. Each case requires $$$O(1)$$$ time, so all cases require $$$O((nm)^2)$$$ time. The states of the dynamic programming can be calculated from top to bottom and from right to left. Moreover, we can only store current and the next row or column. So we only need $$$O(\min(n^2m, nm^2))$$$ memory.
Problem F. Path Reverse
$$$O(n^2)$$$ solution
To solve this problem in $$$O(n^2)$$$, it's enough to iterate over all pairs $$$(p, q)$$$ and for each of them find the answer in $$$O(1)$$$.
In this solution, we must be able to find the distance between every pair of vertices in $$$O(1)$$$. We can precalculate them: just run dfs or bfs from each vertex and get $$$d_{ij}$$$ — the distance between vertices $$$i$$$ and $$$j$$$.
When $$$p$$$ and $$$q$$$ are fixed, each vertex $$$x$$$ belongs to one of the four following kinds:
- $$$x$$$ lies on the path between $$$p$$$ and $$$q$$$, inclusively. This can be checked with this condition: $$$d_{px} + d_{xq} = d_{pq}$$$.
- $$$x$$$ lies in the part of tree behind vertex $$$p$$$, or $$$d_{xp} + d_{pq} = d_{xq}$$$.
- $$$x$$$ lies in the part of tree behind vertex $$$q$$$, or $$$d_{pq} + d_{qx} = d_{px}$$$.
- $$$x$$$ lies on a branch connected to the path $$$p-q$$$. This happens if all three of the conditions above are false.
How can vertices $$$1$$$ and $$$n$$$ be located relative to $$$p$$$ and $$$q$$$? There are 16 cases in general: $$$1$$$/$$$n$$$ (independent) can have one of four relations above (4 choices). The distance between $$$1$$$ and $$$n$$$ changes only in these cases (actually in 8 cases out of 16):
- $$$1$$$ is behind $$$p$$$, $$$n$$$ is on path $$$p-q$$$ or lies on a branch.
- $$$1$$$ is behind $$$q$$$, $$$n$$$ is on path $$$p-q$$$ or lies on a branch.
- $$$n$$$ is behind $$$p$$$, $$$1$$$ is on path $$$p-q$$$ or lies on a branch.
- $$$n$$$ is behind $$$q$$$, $$$1$$$ is on path $$$p-q$$$ or lies on a branch.
As they are identical, consider only the first one. So, $$$1$$$ is behind $$$p$$$, and $$$n$$$ lies on a path $$$p-q$$$ or on a branch. Before the reverse operation the distance was $$$d_{1p} + d_{pn}$$$, and after the swap it becomes $$$d_{1p} + d_{qn}$$$. Problem solved, 2 points are ours.
Solution for a line case
Here our tree is a line, but we must do it in $$$O(n)$$$. The distance changes only when one of $$$p$$$ and $$$q$$$ lies outside path $$$1-n$$$ and the other one lies inside.
First of all, calculate the distance between $$$1$$$ and $$$n$$$ and multiply it by $$$\frac{n(n-1)}{2}$$$. We will find how answer changes after reverse operations, not calculate it from scratch every time.
Let's say $$$1$$$ is to the left of $$$n$$$, and denote the number of vertices strictly to the left of $$$1$$$ as $$$a$$$, and strictly between $$$1$$$ and $$$n$$$ as $$$b$$$.
.... (a slots) .... [1] .... (b slots) .... [N] ....
Let $$$d$$$ be the delta the answer increases by after the reverse. If $$$p$$$ is in one of the $$$a$$$ slots to the left of $$$1$$$, how many slots for $$$q$$$ on path $$$1-n$$$ can produce this delta $$$d$$$? Let's show the pictures for $$$d=1$$$ and $$$d=2$$$:
$$$d = 1$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [ ] [p] [q] [ ] [ ] [ ] [ ] [ ] [N] [ ] [ ]
[ ] [ ] [ ] [ ] [p] [ ] [1] [q] [ ] [ ] [ ] [ ] [N] [ ] [ ]
[ ] [ ] [ ] [p] [ ] [ ] [1] [ ] [q] [ ] [ ] [ ] [N] [ ] [ ]
...
$$$d = 2$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [p] [ ] [q] [ ] [ ] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [p] [ ] [ ] [1] [q] [ ] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [p] [ ] [ ] [ ] [1] [ ] [q] [ ] [ ] [N] [ ] [ ] [ ]
...
Hope you got the pictures. For fixed $$$d$$$, the answer is $$$\min(a - d + 1, b + 1)$$$ (one of the segments with slots ends sooner, that's why there is minimum in the formula). So we add $$$d \cdot \min(a - d + 1, b + 1)$$$ to the total answer.
Deltas can be negative (the distance between $$$1$$$ and $$$n$$$ can decrease). This are the pictures for negative deltas:
$$$d = 1$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [ ] [ ] [q] [p] [ ] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [ ] [q] [1] [ ] [p] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [q] [ ] [1] [ ] [ ] [p] [ ] [N] [ ] [ ] [ ]
...
$$$d = 2$$$:
.... (a slots) .... [1] .... (b slots) .... [N] ....
[ ] [ ] [ ] [ ] [ ] [ ] [q] [ ] [p] [ ] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [ ] [q] [1] [ ] [ ] [p] [ ] [N] [ ] [ ] [ ]
[ ] [ ] [ ] [ ] [q] [ ] [1] [ ] [ ] [ ] [p] [N] [ ] [ ] [ ]
...
Here, the formula for a certain $$$d$$$ is $$$\min(b - d + 1, a + 1)$$$.
Positive $$$d$$$ can change from $$$1$$$ to $$$a$$$, and negative $$$d$$$ can change from $$$1$$$ to $$$b$$$ (by absolute value). For each of these $$$d$$$ we find the answer's delta in $$$O(1)$$$.
Challenge: actually, knowing $$$a$$$ and $$$b$$$, it's possible not to iterate over $$$d$$$ (which would be $$$O(n)$$$), but calculate everything in $$$O(1)$$$. Can you discover the formula?
Solution for a general case
In $$$O(n^2)$$$ solution, we divided all vertices into four classes depending on their location relative to $$$p$$$ and $$$q$$$. Here we will need the similar thing but relatively to $$$1$$$ and $$$n$$$.
Let's say $$$d_{1x}$$$ is the distance from $$$x$$$ to $$$1$$$, and $$$d_{nx}$$$ — from $$$x$$$ to $$$n$$$. Also let's say $$$m$$$ is the distance between $$$1$$$ and $$$n$$$. Then, vertices can be:
- behind $$$1$$$ or equal to $$$1$$$: $$$d_{1x} + m = d_{nx}$$$,
- behind $$$n$$$ or equal to $$$n$$$: $$$d_{1x} = m + d_{nx}$$$,
- strictly inside the path $$$1-n$$$: $$$d_{1x} + d_{nx} = m$$$, but $$$x \ne 1$$$ and $$$x \ne n$$$,
- on a branch, if all three conditions above are false.
Answer changes in two general cases:
- $$$p$$$ is strictly between $$$1$$$ and $$$n$$$ or equal to one of them, and $$$q$$$ is behind $$$1$$$ or $$$n$$$,
- $$$p$$$ is strictly between $$$1$$$ and $$$n$$$, and $$$q$$$ lies on a branch, and the root of the branch $$$z$$$ is strictly between $$$1$$$ and $$$n$$$, and $$$p \ne z$$$.
First case:
Let's iterate over $$$q$$$. Now we have fixed $$$q$$$. How can the answer change?
... [Q] ..... (a slots) ... [1] ... (b slots, P is somewhere on [1, N)) ... [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [ ] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [ ] [ ] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [N] ...
...
... [Q] [ ] [ ] [ ] [ ] [ ] [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [N] ...
For the first row ($$$p=1$$$), the delta is $$$a$$$ (which is equal to $$$d_{1q})$$$, for the second row — $$$a-1$$$, and so on. Finally, when $$$n$$$ and $$$p$$$ are neighbors, it's $$$a-b$$$ (it may be negative if $$$a < b$$$, it's fine). So the result is the sum of consecutive numbers between $$$a$$$ and $$$a - b$$$ and can be found in $$$O(1)$$$.
If you solve this case correctly and completely ignore the second case, you will get 2 points, as this solves the line subtask.
Second case:
Let's again iterate over $$$q$$$. Knowing $$$d_{1q}$$$ and $$$d_{nq}$$$, we can find the branch root $$$z$$$ (as we can calculate the length of the branch, which is $$$\frac{d_{1q} + d_{nq} - m}{2}$$$, where $$$m$$$ is distance between $$$1$$$ and $$$n$$$, $$$m = d_{1n}$$$) and its $$$d_{1z}$$$ and $$$d_{nz}$$$. Here we again have two identical cases (choice between $$$1$$$ and $$$n$$$), let's show one of them.
...
[N]
[ ]
...
[ ]
... [1] ... (a slots, P is somewhere on (1, Z)) ... [Z] ... (b slots) ..... [Q] ...
... [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
... [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [ ] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
... [1] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [p] [ ] [ ] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
...
... [1] [p] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [Z] [ ] [ ] [ ] [ ] [ ] [Q] ...
Here, $$$a = d_{1z} - 1$$$, $$$b$$$ is the branch length minus 1. As shown at the picture, answer changes when $$$p$$$ runs from $$$1$$$ to $$$z$$$, not including $$$1$$$ and $$$z$$$. It is again a sum of consecutive numbers: $$$b + (b-1) + \ldots + (b-a+1)$$$ and again can be calculated in $$$O(1)$$$.
So for each of two general cases, we iterate over all $$$q$$$ and for each $$$q$$$ find the answer is $$$O(1)$$$, which gives the total complexity $$$O(n)$$$.











A small note about the Python solution on D. In Python you don't need to use floats for
instead you can (and probably should) use
int.bit_lengthThis is not just a Python trick. C++20 introduces the function
bit_widthwhich is the same thing as Python'sbit_length.