As I didn't find any blog for this round discussion so posting this blog
Problems :
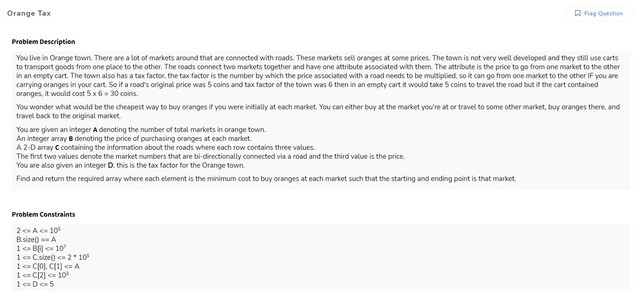
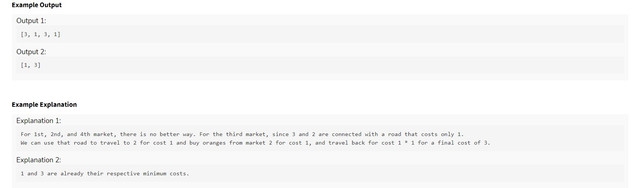
Problem 1
Problem 2
Problem 3
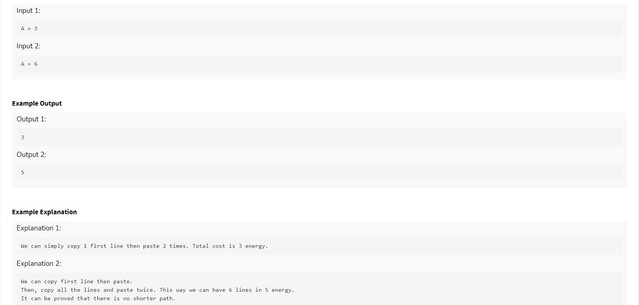
Problem 4
Problem 5
Problem 6
My opinion :
I found problems harder than the previous version of CodeAgon 2021.
Please share your approaches and solution for problems in comments.
PS : Sorry for unclear photos of problems (if anyone have clear photos please share them in comments)














Auto comment: topic has been updated by mon0pole (previous revision, new revision, compare).
This time it was smooth, no mistakes
Not exactly, problem D had weak test cases, always buying the stock on first possible day worked for one of my friend, which is clearly wrong.
Was the intended solution, getting an expression in terms of sqrt(y), and then differentiation and solving quadratic to get the global maxima? I did that
Did you got ac with that? I got WA with this approach.
yes
Can you share your code please?
Differentiating was not necessary, the fact that you got quadratic was enough to claim that one of the extreme values in A would give maximum for a fixed B. so just do these 2*m checks
Shouldn't it be having bitonic nature?
My bad, what I said above is incorrect. I substituted buying date as 4*b*b and buying price as Z — 2*b, which when i plug into the profit expression gives a cubic with negative leading term. So I should have checked the least buying date, latest buying date, and second extremum of this cubic (for each choice of selling quotation), but i guess due to weak tests checking the least and latest buying date itself ACed.
Can u please share how did you solved it.
Vin__ar, Since A[i][0] are at a gap of 4 atleast and there is always a fixed gap between sqrt(A[i][0]) and A[i][1], I feel that taking the first buying day is always optimal. Can you tell me why its wrong
Sure, here's a case A = {{12, 47},{36,44}} B = {{100, 48}} Correct me if I'm missing something.
Atleast this time I didn't have to guess the setter's solution XD.
How to solve problem 1?
For every market $$$i$$$, you can either buy the oranges from the same market or go to one of the markets $$$j$$$, connected to it, get the oranges in minimum possible cost from $$$j$$$ and come back to $$$i$$$. This will incur an extra cost of $$$cost_{ij}$$$ + $$$d*cost_{ij}$$$. You can solve this using Dijkstra's algorithm. Imagine, there is a virtual node connected to all the markets and edge cost is $$$b_i$$$. Also multiply all the original edge weights by $$$d+1$$$. Problem then reduces to finding shortest path from that virtual node to all other nodes.
I have seen this kind of trick somewhere. Can you please share some problem related to this trick, if you can recall?
Sorry, couldn't recall any problem. But generally when I have a solution that is dp but the transitions make a graph with cycles, I try to think if updating the states in the correct order is possible through Dijkstra. So, for this problem, I initially thought $$$ans_i = min(ans_j + (d+1)*cost(i,j))$$$. Then realized that the updates are possible through Dijkstra. That virtual node is a common implementation trick, you can just ignore that and initialize $$$ans_i = b_i$$$ and then do the relaxations in Dijkstra.
This is the exact same problem of Codeagon 2020. problem 1 Just replace the edge weights with cost * (D + 1). Rest everything is exactly the same. And it's more funny when you find the problem on code forces that they copied from in 2020, which they repeated now. link
In problem 2, I wrote dp[A][A]. dp[i][j] denotes I have written i lines and selected j lines which I can paste and then the transitions were easy. Can someone tell me was there any other obvious method to solve this problem?
I was getting TLE for my solution. How do i optimise the loop inside the recursion?
Actually, you don't need to do the loop for more than 2 or 3 copies. I have no formal proof of it, just by intuition I wrote this.
I didn't get your point, are you saying loop is not required for input greater tha 2 or 3?
Can you please explain your dp states and what you are doing in the loop first? I was saying that if you have already copied x lines from the previous step, then there is one possibility to copy j lines from the top (j varies from 1 to the current number of lines written till now) and it will cost j+1. For this j, I am saying that the max value of j can be 2-3. You just need to copy not more than 2-3 lines using this operation as it's always better to use other cheaper methods.
Did anyone solve 4+ ?
How many could you solve? Me 4 (1,2,5,6).
Can you state how to solve problem 5
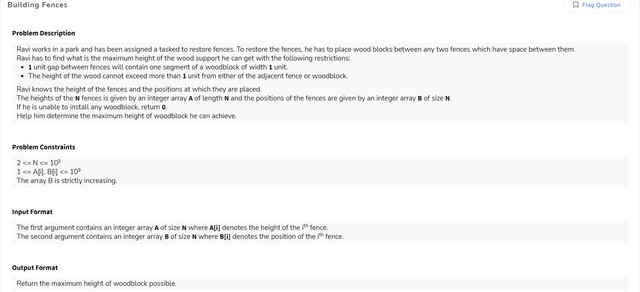
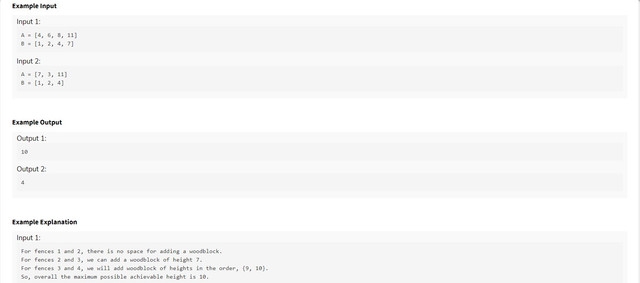
So lets say we are at index $$$i ∈ (1<=i<n)$$$
and suppose $$$ h1=A[i], h2=A[i+1] => x=min(h1,h2), y=max(h1,h2) $$$
$$$ p1=B[i], p2=B[i+1] $$$ and initially $$$ ans=0 $$$
if$$$ (p2=p1+1) => $$$ we can't place a woodblock
else if$$$ (y-x >= p2-p1-1) => $$$ even if we place the woodblock from x in increasing manner we can only reach the height of $$$ x+(p2-p1-1) $$$ so $$$ ans=max(ans,x+p2-p1-1) $$$
otherwise, we can place the wooden block from $$$ x $$$ until we get height of $$$ y $$$ then we can form a pyramid from either side
if remaining places are odd then we can have max height of $$$ y + (remaining/2 + 1) $$$ else we can have $$$ y + (remaining / 2) $$$ height
so $$$ rem = p2-p1-1-(y-x) , ans = max(ans,y+(rem+1)/2) $$$
so we can iterate over the array and find max achievable height in $$$ O(n) $$$
If you find anything wrong correct me
What are your approaches for problems 3 and 4? Here are mine-
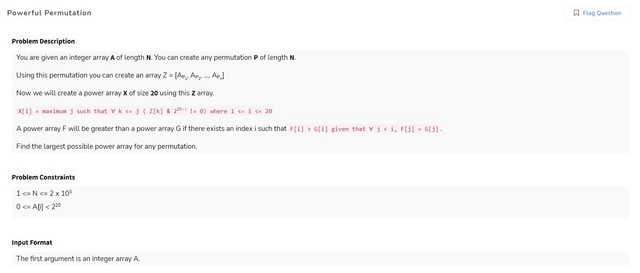
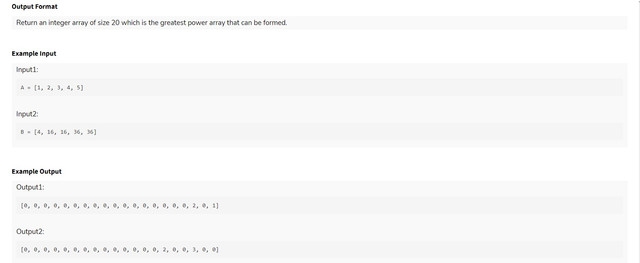
The problem asks us to find the permutation of A that will generate the lexicographically largest array $$$X$$$. We know how we can solve this, if the array was binary (by sorting in non-increasing order). We do a similar thing, but with a twist. For any range of array elements, we can divide it into 2 parts, a good part, where the integers have $$$i^{th}$$$ bit is set, and a bad part, for the remaining integers.
This is nothing but divide and conquer. We iterate through a range, cluster good values first and bad values later, and then iterate through the sub ranges for lower bits. For example we have a range $$$[x,y]$$$. There are $$$z$$$ good elements for bit position $$$i$$$. So we will generate the ans for bit $$$i+1$$$ for ranges $$$[x,x+z], [x+z+1,y]$$$.
Now how do we combine our answers for bit $$$i+1$$$? We can see that if a bad segment exists(for a particular set bit) in between 2 good segments, then the right segment will not contribute to the answer. So we combine values if and only if the entire segment is good for the set bit. In other words, for range $$$[x,y]$$$, if good elements is $$$k$$$, then, $$$ans[i+1] = (k==z) ? z + good[x+z+1,y] : k$$$
Finally, $$$X[i]$$$ will be the value at $$$ans[20-i]$$$ for range $$$[1,n]$$$
The following AC code uses the same thing in an iterative way.
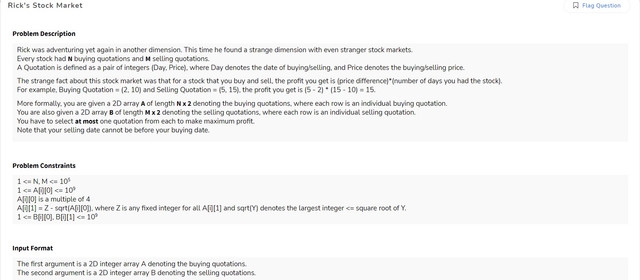
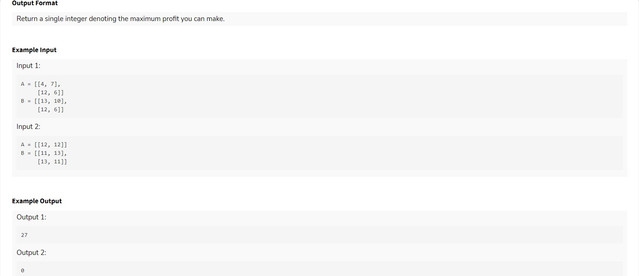
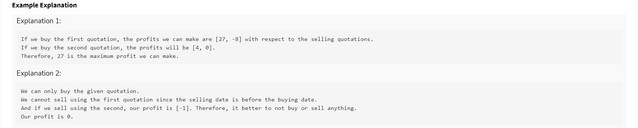
Given an array of cost prices $$$A$$$, and sell prices $$$B$$$, find maximum profit on buying and selling stock at most once.
I used the constraint
A[i][1]=Z-sqrt(A[i][0])to observe according to this, if $$$A[i][0]<A[j][0]$$$, then $$$A[i][1]>=A[j][1]$$$. Usually in such problems, if we consider any $$$B[k]$$$ such that $$$B[k][0]>A[j][0]$$$, then, the function $$$F(x)=(B[k][0]-A[x][0])*(B[k][1]-A[x][1])$$$ is an increasing-decreasing (or decreasing-increasing, but given we needed to find maximum here, I was kinda sure of the former) function for $$$x \in [0,sz]$$$ where $$$sz$$$ is the number of quotations with $$$A[j][0]<B[k][0]$$$. I wrote a few examples on pen and paper and came up with it, so I don't have a solid mathematical proof behind my intuiton. Apologies.So I ran a ternary search to locate the maxima for all sell prices, and compared it to the global maxima. Additionally, I first compressed the arrays so that there are only distinct values in $$$A$$$, and $$$B$$$. So, if there were 2 equal values in $$$A$$$, I chose the smaller price quotation (better to buy at a low), and vice versa for $$$B$$$. The following is my AC code.
If you have any suggestions and/or cases where my approaches fail, do let me know.
For 3rd, I think one can simulate the following greedy procedure:
Take the maximum element = maxx
Pop all occurences of it, and add them to the permutation.
Update all remaining values as x &= maxx.
Repeat.
You will have to do this at most 20 times.
The reason this works is because at each step, we are selecting the lexicographically largest element according to the current active bitmask(mask of bits which have still not encountered a 0)
Any information about ranklist?

Discord Link