The statement:
Given three integers $$$n, k, p$$$, $$$(1 \leq k \leq n < p)$$$.
Count the number of array $$$a[]$$$ of size $$$k$$$ that satisfied
- $$$1 \leq a_1 < a_2 < \dots < a_k \leq n$$$
- $$$a_i \times a_j$$$ is perfect square $$$\forall 1 \leq i < j \leq k$$$
Since the number can be big, output it under modulo $$$p$$$.
For convenient, you can assume $$$p$$$ is a large constant prime $$$10^9 + 7$$$
Notice that in this blog, we will solve in $$$O(n)$$$ for general $$$k$$$ from the original task
For harder variants you can see in this blog [Variants] An interesting counting problem related to square product
Solution for k = 1
The answer just simply be $$$n$$$
Solution for k = 2
Problem
Given $$$n (1 \leq n \leq 10^6)$$$, count the number of pair $$$(a, b)$$$ that satisfied
- $$$1 \leq a < b \leq n$$$
- $$$a \times b$$$ is a perfect square.
Since the number can be big, output it under modulo $$$10^9 + 7$$$.
You can submit here: https://lqdoj.edu.vn/problem/aicprtsp2.
Examples
Algorithm
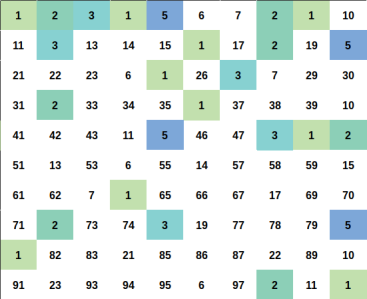
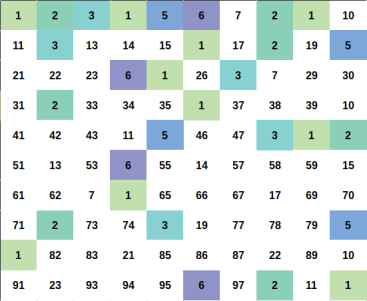
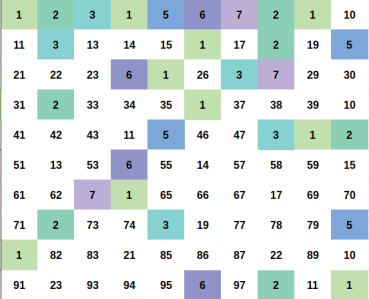
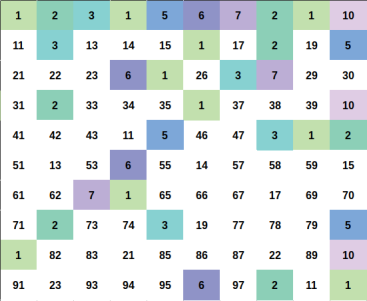
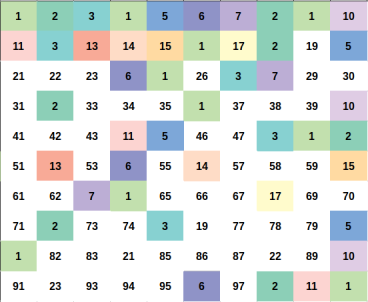
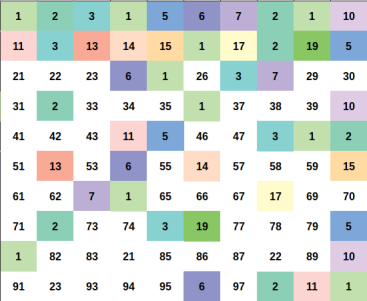
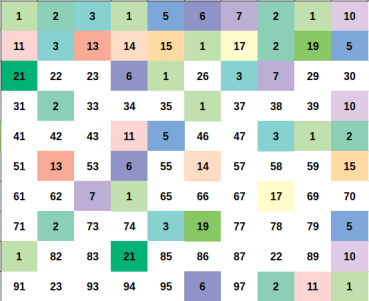
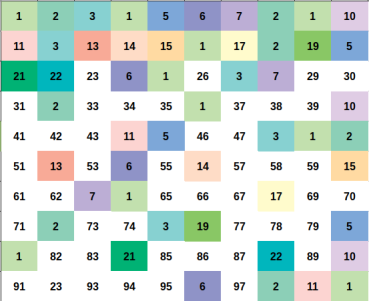
We need to count the number of pair $$$(a, b)$$$ that $$$1 \leq a < b \leq n$$$ and $$$a \times b$$$ is perfect square.
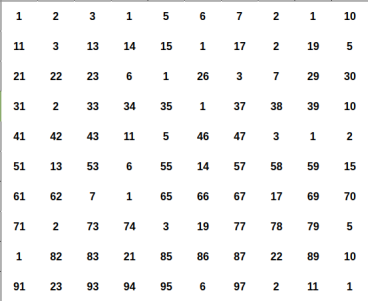
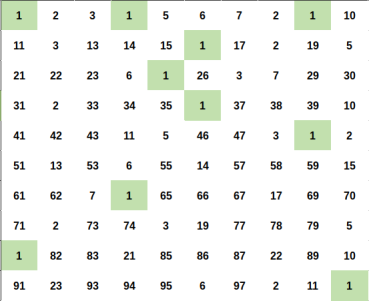
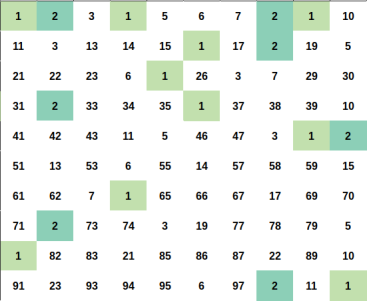
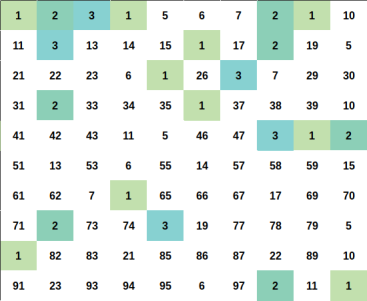
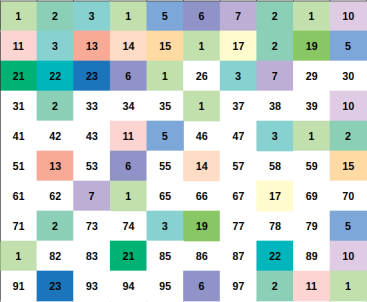
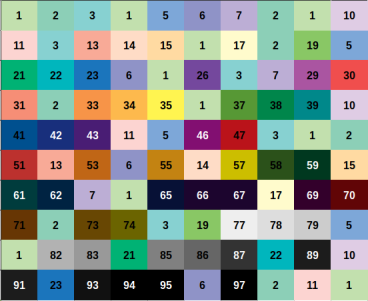
Every positive integer $$$x$$$ can be represent uniquely as $$$x = u \times p^2$$$ for some positive integer $$$u, p$$$ and $$$u$$$ as small as possible ($$$u$$$ is squarefree number).
Let represent $$$x = u \times p^2$$$ and $$$y = v \times q^2$$$ (still, minimum $$$u$$$, $$$v$$$ ofcourse).
We can easily proove that $$$x \times y$$$ is a perfect square if and if only $$$u = v$$$.
So for a fixed squarefree number $$$u$$$. You just need to count the number of ways to choose $$$p^2$$$.
The answer will be the sum of such ways for each fixed $$$u$$$.
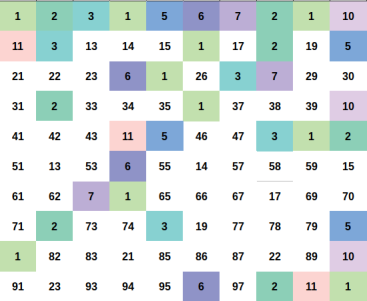
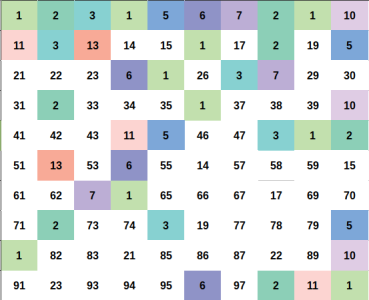
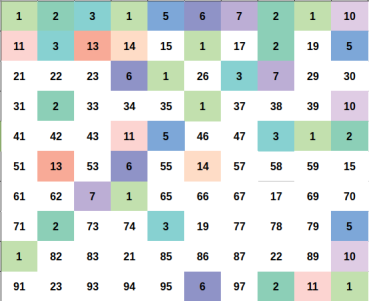
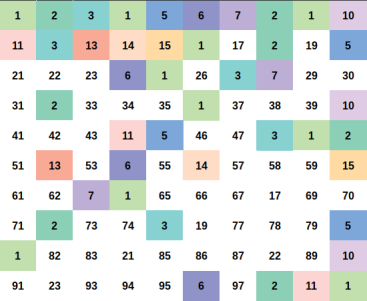
Illustration
Implementation
Complexity
So about the complexity....
For the implementation using factorization, it is $$$O(n \log n)$$$.
For the 2 implementations below, the complexity is linear.
For the last implementation, the complexity is Linear
Solution for general k
Problem
Given $$$k, n (1 \leq k \leq n \leq 10^6)$$$, count the number of array $$$a[]$$$ of size $$$k$$$ that satisfied
- $$$1 \leq a_1 < a_2 < \dots < a_k \leq n$$$
- $$$a_i \times a_j$$$ is perfect square $$$\forall 1 \leq i < j \leq k$$$
Since the number can be big, output it under modulo $$$10^9 + 7$$$.
You can submit here: https://lqdoj.edu.vn/problem/aicprtspk.
For $$$k = 3$$$, you can subimit here: https://oj.vnoi.info/problem/dhbb2020_square.
Examples
Using the same logic above, we can easily solve the problem.
Now you face up with familliar binomial coefficient problem
This implementation here is using the assumption of $$$p$$$ prime and $$$p > max(n, k)$$$
You can still solve the problem for squarefree $$$p$$$ using lucas and CRT
Yet just let things simple as we only focus on the counting problem, we will assume $$$p$$$ is a large constant prime.
Extra Tasks
These are harder variants, and generalization from the original problem. You can see more detail here
A: Can we also use phi function or something similar to solve for $$$k = 2$$$ in $$$O(\sqrt{n})$$$ or faster ?
B: Can we also use phi function or something similar to solve for general $$$k$$$ in $$$O(\sqrt{n})$$$ or faster ?
C: Can we also solve the problem where there can be duplicate: $$$a_i \leq a_j\ (\forall\ i < j)$$$ and no longer $$$a_i < a_j (\forall\ i < j)$$$ ?
D: Can we solve the problem where there is no restriction between $$$k, n, p$$$ ?
E: Can we solve for negative integers, whereas $$$-n \leq a_1 < a_2 < \dots < a_k \leq n$$$ ?
F: Can we solve for a specific range, whereas $$$L \leq a_1 < a_2 < \dots < a_k \leq R$$$ ?
G: Can we solve for cube product $$$a_i \times a_j \times a_k$$$ effectively ?
H: Can we solve if it is given $$$n$$$ and queries for $$$k$$$ ?
I: Can we solve if it is given $$$k$$$ and queries for $$$n$$$ ?
J: Can we also solve the problem where there are no order: Just simply $$$1 \leq a_i \leq n$$$ ?
K: Can we also solve the problem where there are no order: Just simply $$$0 \leq a_i \leq n$$$ ?
M: Can we solve for $$$q$$$-product $$$a_{i_1} \times a_{i_2} \times \dots \times a_{i_q} = x^q$$$ (for given constant $$$q$$$) ?
N: Given $$$0 \leq \delta \leq n$$$, can we also solve the problem when $$$1 \leq a_1 \leq a_1 + \delta + \leq a_2 \leq a_2 + \delta \leq \dots \leq a_k \leq n$$$ ?
O: What if the condition is just two nearby elements and not all pairs. Or you can say $$$a_i \times a_{i+1} \forall 1 \leq i < n$$$ is a perfect square ?














Auto comment: topic has been updated by SPyofcode (previous revision, new revision, compare).
Go get a life pls
agreed
SPyofgame Master when?
.
I've had only a quick look and haven't checked your references yet. Your definitions of $$$f$$$ and $$$g$$$ seem off. As defined, $$$f(49) = \mathrm{size} \{(1, 7)\} = 1$$$ and $$$g(49) = \mathrm{size} \{(1, 7), (49, 49)\} = 2$$$, and $$$g(n) = f(n) + 1$$$, not $$$f(n) - 1$$$. But from the rest of the post it seems likely intended that $$$f(49) = 6$$$ and $$$g(49) = 7$$$. Then in the solution derivation it seems that it should be that $$$\overset{n}{\underset{p=1}{\Large \Sigma}} f(p) = -n + \overset{n}{\underset{p=1}{\Large \Sigma}} g(p)$$$ rather than what is written.
It possible to solve this problem in $$$O(\sqrt{n} \log{\log{n}})$$$ for any $$$k$$$ using a similar idea as that for $$$k = 2$$$. Here's a quick sketch of how to generalize your approach to any $$$k$$$:
Let $$$F_k(n)$$$ be the answer, and let $$$f_k(n) := F_k(n) - F_k(n-1)$$$. Then, clearly, $$$f_k(n)$$$ is the number of valid sequences of length $$$k$$$ ending in $$$n$$$, which is equal to $$$\binom{g(n)-1}{k-1}$$$, where $$$g(n)$$$ is the largest integer whose square divides $$$n$$$, as in your argument. Letting $$$s_k(i) = \binom{i-1}{k-1}$$$, we have by Möbius inversion that $$$f_k(n) = s_k(g(n)) = \sum_{d^2 | n} (\mu * s_k)(d)$$$. Then, as you argue above, we have that $$$F_k(n) = F_k(0) + \sum_{d=1}^{\lfloor \sqrt{n} \rfloor} (\mu * s_k)(d) \cdot \lfloor \frac{n}{d^2} \rfloor$$$. Since Möbius inversion can be done in $$$O(n \log{\log{n}})$$$ for a general (not necessarily multiplicative) sequence of length $$$n$$$, this formula takes the claimed $$$O(\sqrt{n} \log{\log{n}})$$$ when implemented directly.
(EDIT: minor notation cleanup)
It should also be possible to perform the transpose of the Möbius inversion on the sequence $$$(d \mapsto \lfloor \frac{n}{d^2} \rfloor)$$$ and use prefix sums on the sequence $$$s_k$$$ to calculate the answer, which I would intuitively expect to work in $$$\tilde{O}(n^{1/3})$$$. (That transpose looks similar to the DP described in this blog.)
The solution is great. But I still find it hard to understand that the part using Dirichlet Convolution. Can you eleborated more ?
I'm not sure which part you're referring to. Here are my guesses:
If you mean the equality $$$s_k(g(n)) = \sum_{d^2 | n} (\mu * s_k)(d)$$$, this is just the Möbius inversion formula combined with the fact that $$$d|g(n)$$$ if and only if $$$d^2|n$$$.
If you mean performing Möbius inversion on a sequence of length $$$n$$$ in $$$O(n \log{\log{n}})$$$, this is done by factoring the Möbius function. In terms of Dirichlet series/generating functions, this is dividing by the Euler product formula for the zeta function. Since for each prime $$$p$$$ the relevant term can be convolved with in $$$\lfloor \frac{n}{p} \rfloor$$$ steps, this works out to a total of around $$$n \log{\log{n}}$$$ steps.
(EDIT: fixed broken link)
If you mean the part where I wanted to perform the transpose of a Dirichlet convolution on $$$(d \mapsto \lfloor \frac{n}{d^2} \rfloor)$$$, I didn't provide any detail because I hadn't thought through exactly how to do this efficiently yet! It turns out that my intuition was too optimistic, but this can be done in $$$O(n^{2/5})$$$. However, it was easier for me to come up with this algorithm un-transposed, where it turns out to just be a simple modification of the (standard?) $$$O(n^{2/3})$$$ algorithm for calculating prefix sums of a Dirichlet convolution. In this prefix sums of $$$(\mu * s_k)$$$ are needed up to all indices $$$i$$$ for which $$$\lfloor \frac{n}{i^2} \rfloor \gt \lfloor \frac{n}{(i+1)^2} \rfloor$$$. Start by calculating prefix sums of $$$\mu$$$ and $$$s_k$$$ up to these same indices. Then, $$$\mu(i) \cdot s_k(j)$$$ contributes to the value of $$$(\mu * s_k)(i \cdot j)$$$; break these contributions up into three cases:
In the first case iterate over $$$i \cdot j$$$; in the second case iterate over $$$i$$$ and then $$$j$$$; in the third case iterate over $$$j$$$ and then $$$i$$$. That it is possible to do all of these using only the prefix sums I mentioned earlier and that these three cases each take $$$O(n^{2/5})$$$ time to consider, I leave as an exercise. (Transposing this algorithm is still somewhat helpful for extra task H, since the result can be shared between queries. The resulting complexity is $$$O(n^{2/5})$$$ plus the cost of evaluating $$$q$$$ degree-$$$k$$$ polynomials at $$$O(n^{1/3})$$$ points each.)
Regarding the extra tasks:
A, B,: Solved.
C: Redefine $$$s_k(i) = \binom{i+k-1}{k} - \binom{i+k-2}{k} = \binom{i+k-2}{k-1}$$$ and the solution goes through with no other changes.
D: Pretty much solved. The cases where $$$k$$$ is larger than around $$$p$$$ or $$$n^{2/5}$$$ are more annoying, but not really more difficult, assuming $$$p$$$ is prime or at least square-free.
E: Since all perfect squares are positive, we must have that in any valid sequence either all terms are at least 0, or all terms are at most 0. So, this reduces to the positive-only problem.
G: For $$$k > 3$$$ a very similar solution using $$$d^3|n$$$ instead of $$$d^2|n$$$ should just work. For $$$k = 3$$$ I'd need to think about it more.
H: The result at the end of the third spoiler is better than solving the whole problem $$$q$$$ times, but still not that great.
(EDIT: corrected wrong formula from misreading task C)
Great solution. But can I ask that why $$$p \approx n^{2/5}$$$ is also complicated ? Is it for general $$$k$$$ but with $$$O(n^{2/5})$$$ solution ?
It's an issue with claiming $$$O(n^{2/5})$$$ indeed. That's not enough time to naively pre-calculate the factorials and inverse factorials to make calculating the necessary binomial coefficients fast, and how messy the fallback strategies are depends on how large $$$k$$$ is.
*Actually, it's a bit worse than this with FFT-unfriendly primes. But not by enough to really matter for this discussion.
No offensive :( I just want to say that I did not expect it is that hard when $$$p \approx n^{2/5}$$$.