Prepared by Vladik.
Solution: 137274527
Prepared by AleXman111.
Solution: 137274647
Prepared by AleXman111.
Solution: 137274769
Prepared by 4llower.
Solution with $$$O(n \cdot log(n))$$$: 137274837
Prepared by AleXman111.
Solution: 137274954
1609G - A Stroll Around the Matrix
Let's try to solve the problem without asking for changes. Note that in the matrix constructed in this way for the move from (i, j) it is always profitable to go to the cell with the smallest number. This can be seen more clearly in the matrix of the first test case:
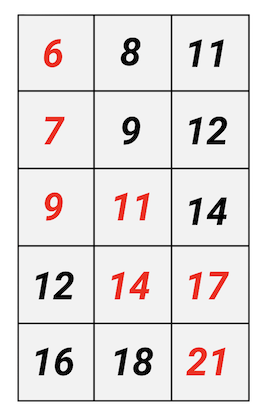
This allows you to solve the problem with complexity $$$O(n + m)$$$, but this is not enough for a complete solution. Let's introduce two new arrays of the difference between the adjacent elements of the arrays $$$da_i = a_{i + 1} - a_i$$$ and $$$db_i = b_{i + 1} - b_i$$$.
Note that our greedy decision turns right out of the cell $$$(i, j)$$$, when $$$da_i > db_j$$$. For clarity, below is an illustration of the turns:
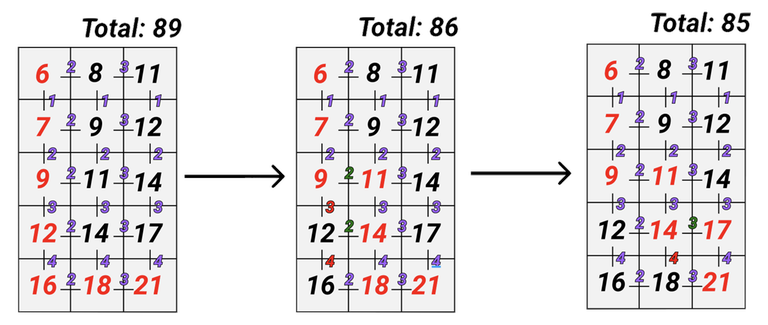
Each time such a turn to the right in the cell $$$(i, j)$$$ decreases our total sum by $$$(da_i - db_j) + (da_{i + 1} - db_j) + \dots + (da_{n - 1} - db_j) = (\sum_{t=i}^{n - 1} da_t) - db_j \cdot (n - i)$$$. Which is actually equivalent to the sum of $$$da_i - db_j$$$ for all $$$da_i > db_j$$$.
Such a sum can be considered by recognizing for each $$$i$$$ by a binary search the last $$$db_j$$$ for which the expression $$$da_i> db_j$$$ is true. This allows us to solve the problem in $$$O(n \cdot log(m))$$$ using the prefix sums of the $$$db$$$ array.
Now let's get back to change requests. Because the size of the $$$da$$$ array is small enough, then we can change the values of its elements by a simple. To store the $$$db$$$ array, you will need to use a segment tree supporting the following operations:
- Adding a number at the suffix (since we are working with an array $$$db$$$, not $$$b$$$, then all elements will change by one number equal to the step of the arithmetic progression).
- Sum of array numbers on array prefix so far $$$element_i < X$$$. ($$$da_i$$$ will act as $$$X$$$).
Prepared by Vladik.
Total complexity: $$$O(q \cdot n \cdot log(m))$$$.
Prepared by budalnik.











If possible do link codes with solution .
added the most understandable solutions.
I solved F by reducing it to a geometry problem. But I only fixed my TLE 5 minutes after the contest ended :rage:
First, for each index, we want to know the largest range on which it's the minimum element, and the largest range on which it's the maximum element. We can precompute all these ranges in linear time with a monotonic stack idea, for example. Let's say the range where $$$a_i$$$ the minimum element is $$$[l_1(i), r_1(i)]$$$ and the range where it's the maximum element is $$$[l_2(i), r_2(i)]$$$. If there's a tie for the minimum (maximum) element in a range, we always pick the first occurrence to be the minimum (maximum).
Now, for each index $$$i$$$, let's consider the set of intervals $$$[l, r]$$$ on which $$$a_i$$$ is the minimum element. We simply require it to be a subinterval containing index $$$i$$$. So the only constraints are $$$l_1(i) \le l \le i$$$ and $$$i \le r \le r_1(i)$$$. If we visualize this in the plane where one axis is $$$l$$$ and the other is $$$r$$$, we simply are describing a rectangle. Similarly, we have a rectangle for the maximum case.
Let's say that a rectangle is red if it came from the minimum case, and blue if it came from the maximum case. First, notice that no two rectangles of the same color intersect, because a range has a unique minimum and maximum by our tie-breaking rule. Our task is to calculate how many lattice points are the intersection of a red and blue rectangle, and both of them have the same "group number", namely the popcount of their corresponding $$$a_i$$$ values.
Let's just offset rectangles according to their group number so that rectangles of different group numbers definitely don't intersect, and rectangles of the same group are offset by the same amount.
The only thing we need to compute is the area of intersection of red rectangles and blue rectangles. It's sufficient to find the area of the union of rectangles, by inclusion-exclusion. We can find the area of the union of these rectangles in $$$O(n \log n)$$$ time with a sweepline and segment tree. Reference for rectangle union problem: https://cses.fi/problemset/task/1741
You can also find the intersection by using a max query segment tree with max frequency.
This is true, but union was better in my case because I can apply ctrl C ctrl V trick.
Cool idea
Have you tried submitting your TLE code using G++17 compiler rather than G++17(64) or G++20(64)?
From what I have experienced, G++17(64) and G++20(64) sometimes make your code 2 times slower, compared to G++17.
During the contest I tried running custom invocation on several compilers but in the end I needed to improve the idea a little further.
Can anyone please explain E in more detail ? I am not able to understand the solution presented in the editorial.
thanks for the feedback, we will try to make it clearer.
I haven't read the intended solution, but here's an explanation of mine, which I find intuitive.
Let's say we have an interval and we don't want it to contain a subsequence $$$abc$$$. We can split the interval in half, and then there are three ways we can do this:
If we're minimizing the number of operations, we should just take the best of all three options.
Now, this gives us a way to combine two nodes of a segment tree into one: we just need to store the answer for each substring of $$$abc$$$.
Implementation: 137243787
Thanks! This was really helpful! Also thanks for the extremely readable implementation.
This solution is way simpler! Thanks a lot!
Thanks, using this hints, I could solve 2400+ problem for first time during upsolve :) I was wondering can we apply similar technique to https://codeforces.com/problemset/problem/750/e also? I saw it is being referred as similar to this one in some comments, so was curious.
Yes, in fact I used a similar idea to solve it. You can see the comments in my solution for more details. 123896956
I can't understand why we choose these 3 cases.
For example why we don't make first half no subsequence of $$$a$$$ and second half have no subsequence of $$$bc$$$, why $$$ab$$$ and $$$bc$$$?
Can u explain why this answer works?
The case you're describing is too restrictive, and it's already handled by my case 1.
I hope it's easy to see why my $$$3$$$ cases all guarantee there will be no $$$abc$$$ subsequence, so I will explain why they cover everything.
Let's say the interval is $$$[l, r]$$$ and the two halves are $$$[l, m]$$$ and $$$[m+1, r]$$$. Also let's say that we marked some characters as deleted, so that there is no subsequence $$$abc$$$. My goal is to show that this arbitrary way of deleting characters falls into one of my three cases. Since I chose the best way in all $$$3$$$ cases, it's optimal.
Let's define $$$i$$$ to be the first non-deleted occurrence of $$$a$$$ in the interval, and $$$j\ge i$$$ to be the first non-deleted occurrence of $$$b$$$ that follows. (In case it's undefined, just say it's $$$r+1$$$). Now, we can split by cases of where the indices $$$i$$$ and $$$j$$$ fall relative to the midpoint $$$m$$$.
We end up with the exact same cases I described.
It's clear now, thanks for this amazing explanation.
For me it helped looking at picture how we can create subsequence in 2 segments:
left segment | right segment:
case 1. nothing | abc
case 2. a | bc
case 3. ab | c
case 4. abc | nothing
OPTION 1: if we delete "a" from left segment, cases 2,3,4 cannot exist so we only delete "abc" from right segment. The reason we delete "abc" and not "bc" is because deleting "abc" <= than deleting "bc" (its because if we can delete "bc" in X moves, we can delete "abc" also in X moves (we delete all "bc" so there is no "abc"), but "abc" can also be deleted by deleting some "a"'s, which may be cheaper)
OPTION 2: if we delete "ab" from left segment cases 3,4 cannot exist, but case 2 can, so we must delete "bc" instead of "abc" in right segment (this will also delete "abc", with the reason above)
OPTION 3: if we delete "abc" from left segment case 4 cannot exist but case 3 can, so we must delete "c" instead of "bc" in right segment
These are 3 options considered by 1-gon, for "ab" and "bc" is similar, just look at:
case 1. nothing | ab
case 2. a | b
case 3. ab | nothing
and do the same.
EDIT: I just realized why we don't consider deleting "b" from left segment and "bc" from right segment: as I said above, deleting "ab" <= deleting "b" :)
Thanks for your explaination
Looking at the 750E and this comment helped me to understand a really interesting solution for this problem using string automata
I agree, string automata is the most straightforward way to solve this problem. The automaton is very simple. A simple computation tells us that the transition monoid has 14 different states, corresponding to strings "", "a", "b", "c", "ab", "bc", "cb", "ac", "ba", "cba", "bac", "acb", "bacb", "abc". (Yeah I was also surprised to see "bacb"). So every string is equivalent to one of these 14 strings in the way it acts on the automaton. Now you can just precompute the $$$14 \times 14$$$ table of transitions, and each node of the segment tree has 14 values, the minimum cost to bring the substring to each of the 14 forms (or $$$\infty$$$ if not possible). The final solution is given by the minimum of all but the last number, corresponding to "abc".
The resulting code is very clean: 138766217
Thank you prof. Jelena Ignjatovic for teaching me Automata Theory, in particular the algorithm to build the transition table. I had no idea I would use it on CF one day.
Here is another solution which I think is fairly intuitive as well and easier to implement than the editorial idea.
For there not to be any subsequence $$$abc$$$, we will have to remove $$$a$$$ from some range $$$[1, i]$$$, $$$b$$$ from the range $$$[i, j]$$$ and $$$c$$$ from some range $$$[j, n]$$$. Or in other words the string will have to satisfy $$$(b|c)^*(a|c)^*(a|b)^*$$$. We will call these the three parts of the string.
For each node of the segment tree lets just store for the minimum number of characters that need to be deleted such that this node's range starts in the $$$l$$$-th part and ends at the $$$r$$$-th part where $$$1 \leq l \leq r \leq 3$$$.
Clearly for a single node, we only need to delete it if we're considering the exact part where it can't be placed, i.e, $$$l = r = 1$$$ for $$$a$$$, $$$l = r = 2$$$ for b, or $$$l = r = 3$$$ for c. Otherwise we can always place it somewhere in one of the parts.
Now to construct the answer for $$$[l, r]$$$ from its child ranges we just need to take the min sum of $$$[l, split]$$$ for the left child and $$$[split, r]$$$ for the right child over all $$$l \leq split \leq r$$$.
Implementation — 137303306. init, combine and main are the important parts. build and update are just standard segtree functions copy pasted from cp-algo.
Could you elaborate what is the intuition behind this? Why do we know that removed characters are not mixed in any way?
Problem D was more an English comprehension test for me :(
Could not agree more. I had a doubt, asked for clarification and got handed with the savage reply "Read the problem statement" XD.
Yes it took me around 45 minutes to decode the answer for second sample test case:(.
Same. It broke the momentum and in the end I couldn't solve D and I slipped to specialist again ;_;
hahaha. Agreed. I asked for "can you explain the second testcase", and got a red "No".
Maybe too nervous during the contest,i unsterstood D right after the contest and thouhght it a easy problem.
MoSalah and VVD4 has same rating
For anyone looking for video editorial, I have made for problems A to D.
Link to the video
What's the expected time complexity for C? I've used seive to find the primes less than 10^6 and then checked how many pairs are possible when the sequence starts from the ith term, but it's taking too long. From my understanding time complexity of seive is O(log(log(n))) that of my remaining script is O(nlog(n)). Can anyone point where I am going wrong?
My Submission
Your code is O(n^2).
In D, how do we know that the way topvals are inserted in the solution above doesn't exceed logN, is it similar to the reason why find of the dsu doesn't exceel logN ?
In E, am I right that the model solution has the intended complexity of O(n log n * 32 * 32), which is more than what seems reasonable?
It seems that you've done some constant optimization because the number of states which make sense is a bit smaller than 2^5, I have no idea how Java users are supposed to pass this task...
I have no idea why the editorial uses the word $$$mask$$$... I found it easier to define $$$dp_{node,l,r} = $$$ minimum cost to prevent $$$s[l, ..., r]$$$ from appearing as a subsequence of the interval corresponding to $$$node$$$ (and assuming that $$$s[l, ..., r - 1]$$$ has already appeared), where $$$s$$$ is the string "abc". Transitions to merge two nodes are straightforward (just three nested loops, yielding $$$20$$$ operations per merge).
I don't quite like the style of the editorial
But I do appreciate the attempt to include solutions with more readable code than usual. I'll give you that
in problem B: can someone tell me why this code fails 137283903, and this code passes 137284479 ?
Expected: 1, Output: 0
In the code that fails, when you replace a character, you correctly check if it was originally in an ABC sequence, but you fail to check if this new replacement causes a new ABC sequence.
Can anyone help me find the time complexity of my solution for problem C?
Submission: 137291865
I am just wondering how this got AC
$$$O(N log log N), N = 1e6 + 7$$$ for initial prime sieve, see: CP Algorithms
$$$O(n)$$$ as you loop through the array, if it is prime, traverse the pointers left and right to exhaust all $$$1$$$s. It is easy to see that each $$$1$$$ will only be read at most 3 times — once for itself, once due to the prime on its left, and once due to the prime on its right.
AC is intended, your time complexity is good.
each 1 will only be read at most 3 times — once for itself, once due to the prime on its left, and once due to the prime on its right.This makes sense now. Thanks!
each 1 will only be read at most 3 times — once for itself, once due to the prime on its left, and once due to the prime on its right.Could you please explain this if you have understood
Edit : Got it
I solved problem E other dp. Notice, that abc exist if and only if exist 'b' between first 'a' and last 'c'. It is beneficial for us to do this: replace the first few 'a', the last few 'c' and all the 'b' between the first remaining 'a' and the last remaining 'c'. Note also that we can assume that we are deleting the symbol, and not replacing it. Because We can replace 'a' and 'b' with 'c', and 'c' with 'a'.
Let's first reduce the task to an array task. Let's create 3 arrays a, b, c, where a[i] = 1 if s[i] = 'a', b[i] = 1 if s[i] = 'b', c[i] = 1 if c[i] = 1. Then what does our answer look like? Answer is $$$\min_{i <= j} (a_0 + ... + a_i) + (b_{i + 1} + ... + b_{j - 1}) + (c_j + ... + c_{n - 1})$$$ Here you can come up with dp, which will consider the answer as O(n), but let's come up with a quick solution right away.
Let's $$$dp[v][i][j]$$$ — answer for node v segment tree if we begin in array i and finish in array j on subsegment. Then, in order to solve the problem, it remains only to learn how to combine 2 vertices. If we recalculate through v1 and v2 $$$dp[v][i][j] = min_{k1 <= k2} \, \, ( dp[v1][i][k1] + dp[v2][k2][j] )$$$ Explicitly recalculation works in $$$O(\Sigma ^4)$$$, but this is optimized to $$$O(\Sigma ^3)$$$, where $$$\Sigma$$$ is the size of the alphabet. Then the whole solution will work for $$$O((n + q \log n) \Sigma ^3)$$$
It would be nice if the editorial for problem A did not just tell what we need to "notice" to solve it, but also provided some kind of a proof. Because for me the proof is not that obvious, even though I know how to prove it now.
I have a time limit in this submission: 137334481
However, when I checked if some elements are infinity, the solution passed: 137334234
I don't really understand why it did, do these if statements really optimize the solution to that extent, and most importantly why?
My solution to F only uses Divide and Conquer. I think it's quite simple, actually.
Suppose we are calculating the answer for segment $$$[l,r]$$$ that passes through $$$mid$$$ and $$$mid+1$$$. For each $$$l\in [l,mid]$$$, find the following: (with two-pointers)
WLOG $$$j<k$$$. Then,
Complexity is $$$O(n\log n)$$$ and independent of $$$a_i$$$.
Can anyone help me understand why my submission for B is getting WA on test 3. My approach is exactly same as in editorial. can't seem to find the edge case. help will be truly appreciated.137250167
you are not considering the possibility that s[pos] may already be equal to c and changes nothing
I believe that case is already covered internally in my code.
if s[pos] is already c and string abc can be formed with the neighbouring characters we insert into the set which causes no change to the set since the set already contains that value.
check this test
5 1
ababc
3 c
Even after reading D for so long I was not able to understand the testcase 2. Now after reading the editorial one thing is clear — that I don't understand the question itself. Any help in understanding the question or testcase 2 is appreciated. Thank you.
In the testcase 2, when you try to link, but they are already in the same set (For example: 1, 4), you get a new chance to link another node.(we must satisfy first 4 condition, but may not to use all 4 chance to link.) So, when our code read (1, 4), we can link 1 and 5, get the set which has five elements. The answer for each i must be calculated independently., so we can sort it and greedily choosing the larger set.
Thank you for the explanation. I think I get it now.
Yeah!Your reply is so great,
Can anyone tell me why am i wrong in this code ? https://codeforces.com/contest/1609/submission/137238591 Thanks you.
I have alternative perhaps slightly complicated solution for F. However most of the complexity comes from the stringent memory limit. We first iterate over what is maximum element. To find what subranges $$$u$$$ is maximum for, we just need to find closest left element that is larger($$$l-1$$$) and closest right element that is larger($$$r+1$$$). Now we need to find total subarrays such $$$bits(\min(a[l\ldots r])) = bits(a[u])$$$, where $$$bits$$$ is number of set bits.
Let us let the left ending of subarray be $$$l \le l' \le u$$$. Let us now find 2 other arrays as precomputation.
rhtmin[i]: This tells us the index of closest element to the right of $$$a[i]$$$ that is smaller if it exists and $$$n$$$ otherwiserhtcnt[i]: This tells us for how many $$$i \le x \le n-1$$$ is such that $$$bits(a[i]) = bits(\min(a[i\ldots x]))$$$Let us now find the number of $$$r'$$$ such that $$$l \le l' \le u \le r' \le r$$$ such that the the number of bits is the same as in $$$a[u]$$$. We can keep a rolling minimum while iterating $$$l'$$$ from $$$u$$$ to $$$l$$$. Lets use
rhtminon the minimum element to find till what value of $$$r'$$$ will the minimum be on the left side of the array. Using this we can check if should add these subarrays or not.Now we need to use the next trick. We want to find when will the minimum become an element with $$$b$$$ bits. If we do that we can use
rhtcntto compute the answer. The minimum from $$$i$$$ will change atrhtmin[i]. Therefore when an element is found with $$$b$$$ bits is the same for $$$i$$$ andrhtmin[i]except when $$$b = bits(i)$$$. So if we iterate from $$$n-1$$$ to $$$0$$$ and copy the positions we find bit $$$b$$$ it will be fast enough. However as the memory limit does not allow us to make array of size $$$64n$$$ we need to do some memory optimisation.Instead we store when the next element with $$$8k \le b \le 8k + 7$$$ bits appears for each $$$k$$$, and then for an element with $$$8k + i$$$ bits we also store where the next element with $$$8k + j$$$ bits appears. This has optimised memory usage to $$$16n$$$ instead. Now to find the next element with $$$b$$$ bits, we first find an element whose bits $$$b'$$$ satisfies $$$\lfloor b'/8\rfloor = \lfloor b/8\rfloor$$$, and then we find an element with exactly $$$b$$$ bits from the element with $$$b'$$$ bits. This finds the answer in $$$O(1)$$$ still.
Ok now we have found when the number of bits in the minimum becomes $$$b = bits(a[u])$$$. Using
rhtcntwe get the answer for number of subarrays $$$l \le l' \le u \le r' \le n$$$ such that $$$bits(\min(a[l'\ldots r]) = b$$$.To remove the extraneous arrays, we will first have to find the minimum closest to the edge of $$$r$$$. This can be done effortlessly with binary lifting on $$$i \to rhtmin[i]$$$. This used $$$20n$$$ memory which is too much for us. We optimise this by using quaternary lifting which will only use $$$10n$$$ memory at the cost of an extra $$$3/2$$$ factor in runtime.
Ok now we have the closest element to the edge($$$r_m$$$). This will remain constant until the minimum on the left side becomes less than $$$r_m$$$, in which case the minimum of all subarrays is a trivial case and is constant. Let us break $$$r_m$$$ into two cases. If it has $$$b$$$ bits we can easily subtract its
rhtcntto remove extraneous $$$r'$$$. We just add the answer for $$$r_m \le r' \le r$$$ back.If its not, we need to find where is the next time the minimum has $$$b$$$ bits, which will be outside the array and we can simple subtract its
rhtcntto remove extraneous values. All we need to do is the earlier trick again to find the next element with $$$b$$$ bits from $$$r_m$$$ and subtract itsrhtcntto get the answer.We can do the exact same iteration for $$$u \le r' \le r$$$.
If we do it for the smaller of the 2, we will do not more than $$$O(n\log{n})$$$ iterations. If you think of the maximum of an array splitting it into two like some sort of divide and conquer it is clear that this is the case.
And using that we can get the solution in $$$O(n\log{n})$$$.
Solution
I think the memory limit for problem F is too small so that In my solution can't use prefixsum but just can use persistence segment tree. Such as https://codeforces.com/contest/1609/submission/137397827 and https://codeforces.com/contest/1609/submission/137397769
"A little later"
why "Tutorial is not available" for problem H?
It's available now
Edit : mistake from my part, sorry
I have a question in problem E. The code you added to the tutorial doesn't define the following base cases: if we are at the node that contains one character and let's say it's "a" we define seg[ver].dp[1] = 0 but we don't define the case if we replaced the character with "b" or "c". Therefore, instead of defining seg[ver].dp[2] = seg[ver].dp[4] = 1, we are defining seg[ver].dp[2] = seg[ver].dp[4] = inf. How does the solution works even with this? Note: both cases will get accepted so why it doesn't make a difference?