The problem is you have n line segments, where n is upto 10^6 and you should count least amount of rays starting from origin (0, 0) necessarry, so that each line intersects with at least one ray.
The solution to the problem is radial sweep. First sort the endpoints of the line segments by angle and then do a simple sweep, in which if we encounter the end of some line, we do eitherbof two things:
create a ray which goes at a angle of the encountered endpoint from origin and we also increase the answer by 1.
we have already created ray with angle between the angle of start of the current line segment and the end of the current line segment, in such case we do nothing since there is already a ray going through that line segment
And in the last sentence of the second scenario is where my program fails. Sometimes you should cast a ray, for example if you have following two lines and you are on point D in your sweep and have already gone through points CBA in that order:
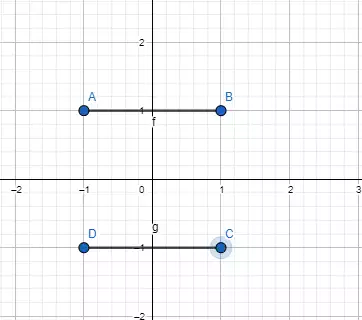
In this moment my mentioned program decides to not do anything, since the angle st which we have casted a ray through point A is between angles of point D and C, if we sort using the function atan2l.
Unfortunately, I cannot figure out how to solve this edge, case. I have, by hand, found out that there are numerous such cases, but I can't make my program solve them and I can't even describe these cases or group them by some characteristic which would help me solve them.
Any help with that would be aprreciated. Thank you very much.









