Before the tutorial, I would like to thank shiven, socho and animeshf for their valuable comments and for improving the tutorial.
Definition of Bridges
Bridges are those edges in a graph, which upon removal from the graph will make it disconnected.
Pre-Requisites
Finding the bridges in a graph.
Introduction
The idea of a bridge tree is to shrink the maximal components without a bridge into one node, leaving only the bridges of the original graph as the edges in the bridge tree.

In the above image, the bridges of the graph are marked in red. They are the edges between the nodes $$$(3, 4)$$$ and $$$(3, 9)$$$. The maximal components without a bridge are $$$[1, 2, 3]$$$, $$$[4, 5, 6, 7, 8]$$$, $$$[9, 10, 11,12]$$$.
Thus, the bridge tree of the graph will become as follows:
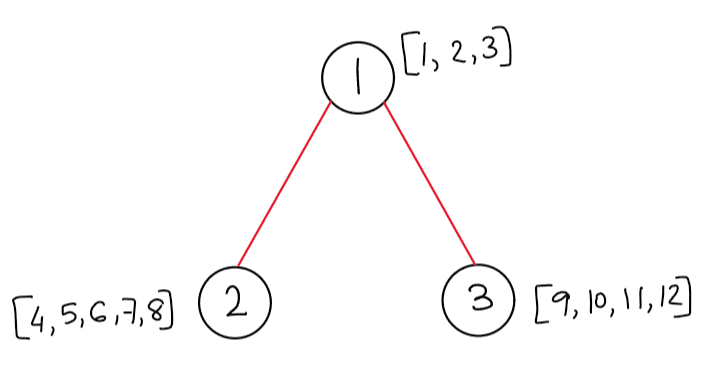
The bridge tree only has $$$3$$$ nodes. The nodes $$$[1, 2, 3]$$$ in the original graph have been shrunk to node $$$1$$$, nodes $$$[4, 5, 6, 7, 8]$$$ have been shrunk to node $$$2$$$, and the nodes $$$[9, 10, 11, 12]$$$ have been shrunk to node $$$3$$$.
Note: Throughout the tutorial, we assume that the given graph is undirected, unweighted and connected.
Properties of the bridge tree
All the bridges of the original graph are represented as edges in the bridge tree.
The bridge tree is connected if the original graph is connected.
The bridge tree does not contain any cycles.
The bridge tree will contain $$$\le N$$$ nodes, where $$$N$$$ is the number of nodes in the original graph.
The bridge tree will contain $$$\le N - 1$$$ edges, where $$$N$$$ is the number of nodes in the original graph.
Pseudocode for making the bridge tree
dfs(int node, int component_number) {
component[node] = component_number //All nodes with the same component number will be shrunk into one node in the bridge tree. This is because we aren't traversing a bridge, and thus, "shrinking" the components without a bridge to one node in the bridge tree.
vis[node] = true //so that we don't visit this again.
for every adjacent edge such that the edge is not a bridge {
next = other endpoint of the edge
if vis[next] = true: continue //already visited this node.
dfs(next, component_number);
}
}
main() {
Find all the bridges in the graph //check the pre-requisites section of this blog for this
for i in 1, 2, 3, ..., n and vis[i] = false {
call dfs(i, unique_component_number) //ensure the component number is unique. A simple way to do it is just by incrementing it by 1 whenever you are calling the dfs function.
}
The time complexity of making the bridge tree
In this section, $$$N$$$ stands for the number of nodes and $$$M$$$ stands for the number of edges in the original graph. The bridges in the graph can be found in $$$O(N + M)$$$. The time complexity for the DFS function is $$$O(N + M)$$$. Note that we can store the ID of the edge alongside the adjacent node in the adjacency list. We can have an array isBridge, and mark isBridge[edge] = true for every edge which is a bridge. During the DFS, just check if the current edge is marked as a bridge using its stored ID.
Thus the total time complexity will be $$$O((N + M) + (N + M))$$$, which is equivalent to $$$O(N + M)$$$.
Sample problem
We are going to solve this problem.
Let us understand the statement first.
There is a connected, unweighted, undirected graph with $$$N$$$ nodes and $$$M$$$ edges.
According to the statement, for some fixed starting node $$$s$$$ and ending node $$$t$$$, your friend will place a boss in each passage such that it is impossible to travel from $$$s$$$ to $$$t$$$ without using this passage. The word impossible tells us that the bosses can only be placed on bridges.
Solution
Since we are only concerned regarding the bridges of the graph, we can compress all the maximal components without a bridge into a single node to get the bridge tree of the graph. The bridge tree of the first sample input is depicted below.
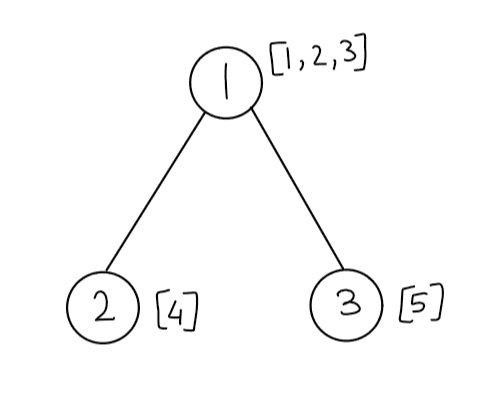
You can see that the nodes $$$[1, 2, 3]$$$ in the original graph are shrunk to node $$$1$$$ in the bridge tree. Similarly, node $$$[4]$$$ is shrunk to node $$$2$$$ and node $$$[5]$$$ is shrunk to node $$$3$$$.
This makes the original problem a lot easier. The only thing left is to choose a path from one node in the bridge tree to the other so that the number of edges (bridges in the original graph) along the way is maximum. This can be solved by finding the diameter of a tree.
You can find my solution here.
Extra Exercise
Can you answer queries of the form find the number of bosses we need to place between fixed $$$s$$$ and $$$t$$$?
Other Problems
Feel free to suggest any other problems! I'll add them to this section.











Amazing blog!
The blog by -is-this-fft- : [Tutorial] The DFS tree and its applications: how I found out I really didn't understand bridges is an amazing blog on bridges.
It has the explanation to the problem: 231E — Cactus which can be solved using the bridge tree approach.
There a small correction too: in the pseudo-code, it should be
dfs(next, component_number);Thanks a lot! Fixed the typo and added the problem.
Thanks for such a wonderful content
Nice blog.
Thanks.
I was solving the sample problem and I independently came up with the idea of compressing a graph into a bridge tree. Lo and behold, I stumble upon this post that validated my solution idea.
What is wrong with this comment? Why are people downvoting it?
Problem J here is also based on Bridge-Tree
Nice Blog'
You can add two problems
100676H - H. Capital City This one needs you to think greedy
100712H - Bridges This one is standard and easy to get the answer
I solved them by constructing a tree with myself as I didn't know there was something called Bridge Trees
so my code will be so long but I will say what I use in it
use Tarjan for bridges to get bridge edges in the graph
then I build a graph using DSU with edges that do not bridges
then i mark for every connected component what is the min node in it (must make this for the first problem)
after that, I build the tree with edges that are bridges but I make sure for every node I get the minimum node in his CC
solutions:
my solution for the first problem Here
my solution for the second one Here
so long code but it's okay for me as I don't know this blog before
two problems are so good to solve
feel free to ask about anything in it