320A - Magic Numbers
Although the input number is very small, solving the problem for arbitrary length numbers using strings is easier. It's easy to prove that a number meeting the following conditions is magical:
- The number should only consist of digits 1 and 4.
- The number should begin with digit 1.
- The number should not contain three consecutive fours (i.e. 444).
Here is a sample implementation in C++:
#include <iostream>
#include <string>
using namespace std;
bool is_magical(string number) {
for (int i = 0; i < (int)number.size(); i++)
if (number[i] != '1' && number[i] != '4')
return false;
if (number[0] == '4')
return false;
if (number.find("444") != number.npos)
return false;
return true;
}
int main() {
string number;
cin >> number;
if (is_magical(number))
cout << "YES" << endl;
else
cout << "NO" << endl;
return 0;
}
320B - Ping-Pong (Easy Version)
Imagine the intervals as nodes of a graph and draw directed edges between them as defined in the statement. Now answering the second query would be trivial if you are familiar with graph traversal algorithms like DFS or BFS or even Floyd-Warshall!
Here's an implementation using DFS: 3951145
And here's an implementation using BFS: 3947426
Finally an implementation using Floyd-Warshall: 3945330
319A - Malek Dance Club
Solving this problem was easy when you modeled the assignment with two sets of points numbered from 0 to 2n - 1 (inclusive) paired with 2n line segments. Each line segment corresponds to a dance pair. And each pair of intersecting lines increase the complexity by one.
Imagine you now the solution for binary string x. Now we want to calculate the answer for 1x and 0x easily. Look at the figure below:
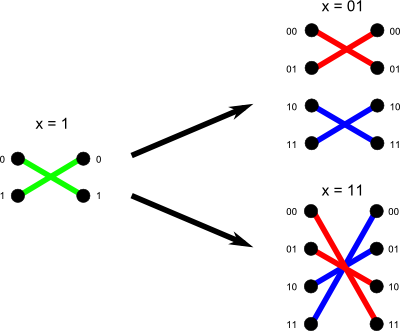
The figure shows what happens in a simple case. Whenever you append 0 before x the same structure appears twice in the result. But whenever you append 1 before x the same structure appears twice but the first half of points in right column are swapped with the second half. This increases the number of intersections by size of first half times size of the second half.
So if x has length n and f(x) is the complexity of the assignment then we have:
- f(0x) = 2f(x)
- f(1x) = 2f(x) + 22n
An interesting fact is that f(x) is equal to x2n - 1.
319B - Psychos in a Line
Will be fixed :)
Let's find the murderer! Well, if you look close you see that each psycho is murdered by the nearest psycho on his left which has a greater id.
Now let ti be the number of the step which i-th psycho in the line is murdered (not the psycho with id equal to i). Assume j-th psycho in the line be the nearest psycho with a larger id than i-th psycho in the line in his left. As we know j-th psycho kills the i-th psycho. We also now that this happens when all psychos between j and i have been killed. So ti = max(tj + 1, ..., ti - 1) + 1.
Now we have a simple O(n2) solution using the above observations. To make things run faster you should be familiar with a classic problem. This problem asks to find the nearest greater element to the left of each element in a array. This problem has a O(n) solution. You can solve it yourself or read about it here.
After knowing about all these things it wouldn't be hard to figure out a way to solve this problem efficiently. Here is a cute implementation of what is described above: 3945963
319C - Kalila and Dimna in the Logging Industry
This problem is equal to finding the minimum cost to cut the last tree completely. Because any cutting operation can be done with no cost afterward. Let dpi be the minimum cost to cut the i-th tree completely. It's easy to figure out that we can calculate dpi if we know the index of the last tree which has been cut completely (j-th tree). Knowing this dpi would be equal to dpj + bjai. So dpi = minj = 1..i - 1(dpj + bjai).
Using the above information the problem has an easy dynamic programming solution in O(n2). There's a known method which can be used to improve recursive relations with similar form. It's called Convex Hull Trick. You can read about it here.
319D - Have You Ever Heard About the Word?
TODO
319E - Ping-Pong
TODO









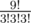 possible permutations of the string AAABBBCCC which tells us how to combine the steps of different types. Switching on the lights is done uniquely for types 1 and 3. But for type 2 each time we have to possible options until we're left with one off light. So there are
possible permutations of the string AAABBBCCC which tells us how to combine the steps of different types. Switching on the lights is done uniquely for types 1 and 3. But for type 2 each time we have to possible options until we're left with one off light. So there are 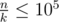 there will be at most
there will be at most 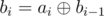 and
and 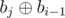 . So we know that all elements of
. So we know that all elements of 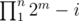 and this is the answer to problem.
and this is the answer to problem. ) and both of them got verdict Wrong answer on test 33. Here are the submissions:
) and both of them got verdict Wrong answer on test 33. Here are the submissions:
