Apologies for the immense lack of math typing — this dummy have precisely 0 idea of how that works out (whoops). Google Sheets that sorts IOI task by amount of AC, average score, max score and stuffs, definitely not hand — typed by yours truly over 3 hours or something: https://docs.google.com/spreadsheets/d/14v9jfFU0hZ47uAvut27_YdZ9FQmp78rP7Rm48tRzPQQ/edit?usp=sharing (Data taken from https://stats.ioinformatics.org/tasks/)
I know, this is definitely a weird thing for a Gray to make a blog out of all things, but yeah. For some reason there's no official editorial even after 1.5 months since the official contest, and no discussion blogs as well. So, yeah, I want to bring this up in order to actually see people discussing about the tasks of IOI23, as the task discussion blogs are always fairly interesting (to read) for me. Besides, I would love to see people actually explaining their ideas (how do you people even come up with that 40-line O(n^2) solution for Soccer, WHY is the model solution for Beech Tree only 100 lines long, what even is the 400+ lines solution for Closing Time,...).
So, yeah, please use the comment section of this blog for discussing about the contest tasks — for those who still cares, 1.5 months after all is said and done.
===============
Now, for my solution of IOI23 Day1 P1:
- Overview: Solving this task by myself is certainly an experience, seeing that I can actually solve a decently hard, non-trivial IOI task by myself, without recieving any hints or reading any model solutions whatsoever is a good thing for my ego.
- The task itself is possibly the best tree — related task that I've seen out of all the IOIs from 2010 onwards or something as it perfectly fits every single criteria of a "fun" task for me: Lots of observation, no advanced data structures needed, and not a pain to implement. Kudos to E869120 for creating such a fantastic task, definitely the best task that my Gray heart has ever seen so far.
(To the creator(s) of this task or ISC members, if you somehow read this: What is the intended solution for this task? DP + optimizing by data structures or greedy with pq?)
As for the task itself:
- According to the statistic from the above sheet, this task is among the hardest P1s — only losing to some infamous, horrendously difficult task like Archery and whatnot. So, yeah, definitely not trivial.
Required algorithms (?)/ ideas for each subtasks (in the solutions that I could come up for each subtasks, if any):
- Subtask 1: Greedy
- Subtask 2: Bruteforce
- Subtask 3: Bruteforce + 2 Pointers
- Subtask 4: ??????
- Subtask 4.5 (for N <= 200000): Greedy, Priority Queue
- Subtask 5: Greedy + Bitmasks Bruteforce + DFS/BFS
- Subtask 6: ???????
- Subtask 7: ???????
- Subtask 8: Standard Dynamic Programming + DFS/BFS
- Subtask 9: Priority Queue + Greedy + DFS/BFS
Do note that I will go through the subtasks in a weird order, so that the explaination could become as understandable and non-mind-boggling as possible. (if you don't want to read the entire process of coming up with the algorithm and would only want to see my solution, it is here: oj.uz submission)
Part 1: Easy subtasks (Subtask 2 and 3)
We can make the following observation to change the way we view this problem:
Observation 1: Instead of "assigning closing times to all cities", we now think about the problem as: "There are N "strategic positions", all initially at Lv0. We can then proceed to upgrade some to Lv1 from Lv0 at a cost, the same applies with upgrades from Lv1 to Lv2. Given a budget K, find the maximum amount of upgrades we can make".
How this changes the way we approach the problem:
- When we look at the cities as points where we have to pay a certain cost to "upgrade" to the next level, it is now obvious that the "cost" to upgrade city i from Lv0 to Lv1 is the distance from i to the closer city out of A and B. Similarly, the "cost" to fully upgrade city i from Lv0 to Lv2 is the distance from city i to the further city out of A and B. Here, the "level" of a city is the amount of "important cities" (literally just A and B) that we could reach from i.
- More precisely: Let DistX[i] and DistY[i] be the length of the path from city i to city X and Y, respectively. Let Cost1[i] and Cost2[i] be the cost to "upgrade" city i from Lv0 to Lv1 and Lv1 to Lv2, respectively. It is trivial to see that Cost1[i] = min(DistX[i],DistY[i]), and Cost2[i] = max(DistX[i],DistY[i]) — Cost1[i] (as we're upgrading a city from Lv0 to Lv1, THEN from Lv1 to Lv2).
Observation 2: For the line subtasks, there could only be 2 "configurations" of levels of cities:
Position: 0 1 2 X 4 5 6 Y 8 9
Config 1: 0 0 1 1 1 0 1 1 1 0
Config 2: 0 0 1 1 1 2 2 1 1 1
Basically, the 2 configurations could be described as follows:
Config 1: A segment (l,r) with l <= X < Y <= r where all cities are upgraded to Lv1. Then, we pick a segment (a,b) with X < a <= b < Y, and rollback all upgrades made to cities in the range (a,b) from Lv1 to Lv0.
Config 2: A segment (l,r) with l <= X < Y <= r where all cities are upgraded to Lv1. Then, we pick a segment (a,b) with l <= a <= b <= r, and upgrade all cities in the range (a,b) from Lv1 to Lv2.
At this point, the O(N^4) solution to subtask 2 is obvious: Just bruteforce through all range (l,r), then pick a range (a,b) to either upgrade all cities in (a,b) to Lv2, or rollback the upgrade to Lv0. Count the total amount of upgrades, and then check whether we have enough budget to make all of those upgrades. We can quickly calculate the cost for all upgrades by using prefix sums (what a suprise).
Let the cost of upgrading all cities in the range [l,r] from Lv0 to Lv1 be B. To achieve an O(N^3) algorithm for subtask 3, we now observe that: If B<K, there is no reason to not try to upgrade some cities from Lv1 to Lv2, so we would try to pick cities where the cost to upgrade them from Lv1 to Lv2 is cheapest, so that we could upgrade as many cities to Lv2 with the remaining budget as possible. Otherwise, if B<K, we will have to undo some upgrades, and as we would want the total amount of upgrades to be as high as possible, we will have to only "rollback" the most expensive upgrades. The statement requires the set of upgraded cities to form at most 2 continious subsegment, which means that, seeing from the previous subtask, every single change made to the original operation "Upgrade all cities in range [l,r] to Lv1" forms a continious subsegment of the range [l,r] itself. As we want to maximize/minimize the amount of changes (depending on the cases), we can simply use 2 pointers to greedily search for the longest/shortest subsegment of Cost2/Cost1 to upgrade/rollback while still satisfying the budget constrain. Using 2-pointers, we can achieve a runtime of O(r-l) for each segment [l,r], which gives us an average runtime of O(N^3).
Part 2: A strange Bitmask subtask, and the first intuition to the DP solution (Subtask 5)
From the constrains of N, it is obvious that this is a Bitmask Bruteforce subtask. However, considering the fact that we have 3 possible states for each city (leave at Lv0, upgrade to Lv1, upgrade to Lv2), and 3^20 is a bit larger than 10^9 at least, just bruteforcing everything isn't possible. We'll have to find a way to make the time complexity 2^n * (something), somehow. Turns out, there is indeed a way
Let's add some new definitions first:
Let's add an arbitrary city M at the perfect midpoint of the path between X and Y
We now call a city i "bounded" if the path from i to X doesn't go through Y and vice versa. (For example, in the following image, every city in the circled region is "bounded"
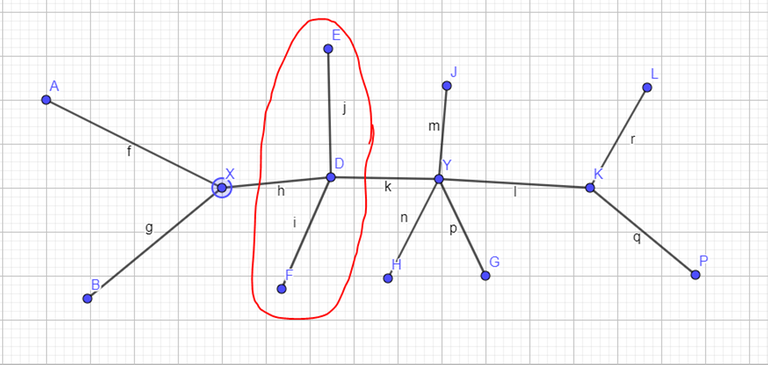
Observation 3.1:
We can now make the following observations about the value of Cost2[i] among all cities:
1) For each city i in the "main line" (the path from X to Y), the value of Cost2[i] increases the further city i is away from city M
2) For each city that isn't on the main line but is "bounded", the value of Cost2[i] of that city is equal to the value of Cost2[i] of the first city that city i encounters when trying to "move" towards the main line. In other words, for each city i on the path from X to Y, all cities that branches out from i has their Cost2 equal to Cost2[i] (for example, in the image above, city H, G and J all branches out from Y)
3) For all cities i that aren't bounded, their Cost2 is equal to DistX[Y]. Basically, we consider all "unbounded" cities to be branching out from X and Y
From the previous observations of the values of Cost2[i] among all cities, we can see that:
Observation 3.2: If we greedily pick cities by their Cost2 from lowest to highest, after every single step, we'll end up with all picked cities forming a single connected component, which is suitable for the secondary constrain (if city i is "visitable" from X, every city on the path from X to i must be "visitable" from X as well).
Proof: Assuming that we're picking a city that branches out from a city i on the XY — path. Then:
Case 1: If there is still an unpicked city which branches from i, we will pick it next. As this newly picked city lies on the same branch from the main path as the last picked city, there always exist a way to pick this city so that it is right next to a previously picked city.
Case 2: Otherwise, the cheapest unpicked city would be either directly to the left or directly to the right of the segment that we've already covered on the XY — path, as they are the only candidate for the next smallest distance to M. For example, on the image above, after we're done with upgrading city D, I, F to Lv2, the next candidate for "closest city to city M" could only be either X or Y. Thus, we can just pick this city, expand our connected component of Lv2 cities, and repeat Case 1 again with this newly maxxed out city on the XY path.
With this observation in mind, we could come up with an O(n * logn * 2^n) solution that goes something like this:
- Step 1: Of course city X is reachable from city X and city Y is reachable from city Y, so pick those 2 first.
- Step 2: We start bruteforcing through every way of choosing cities (aside from X and Y) to "upgrade" to Lv1. We now check the connected components created by those cities:
1) If there is an connected component that doesn't have both X and Y, this configuration is definitely not valid.
2) If there are 2 connected component — one contains X, the other contains Y, the answer could be valid, but only if all cities are upgraded to Lv1. We can think about this as "applying a Level Cap of 1" to all cities, instead of the usual 2. Check if it fits the budget and if it does, compare it to the current optimal answer
3) If there are only 1 connected component, which includes both X and Y, we can bring the level cap back to 2 now. With the pre-picked cities to upgrade to Lv1, we greedily choose the cheapest cities to upgrade from Lv1 to Lv2, as long as it still fits in our budget. Once the budget is no longer sufficient, compare the current total amount of upgrades to the current optimal answer, and change it accordingly. We can implement the process of "choosing cities to upgrade to Lv2 from Lv1 out of already picked cities" with a priority queue, by throwing the -Cost2 of all chosen cities into the priority queue (I push -Cost2[i] into the priority queue instead of Cost2[i] because I don't want to spend additional time defining a new structure, and to abuse the built in max heap function). When we upgrade a city to Lv2, we add into the budget the value that is currently at the top of the priority queue, then remove it from the priority queue.
Time complexity: O(2^N * N log N)
Part 3: The funniest DP solution to an IOI task so far (Subtask 4, 6, 7, 8)
After subtask 5, we could make yet another observation about the value of Cost1[i] among all cities:
Observation 3.3: As long as we have upgraded each city on the XY — path at least once and keep picking the cheapest un-upgraded city to bring to Lv1, the set of upgraded cities would always form a single connected component.
Proof: Let's consider an arbitrary city I. Also, let's remove the restriction "if I is reachable from X, every city on the path from X to I must also be reachable from X". Without loss of generality, let's assume that the closest city out of X and Y to city I is X. Now, the value of Cost1[I] is DistX[I]. Now, if there exist a city C which lies on the XI path and is unupgraded, we could choose to not upgrade city I to Lv1 and upgrade city C instead. As city C lies on the path from X to I, DistX[C] < DistX[I], which means Cost1[C] < Cost1[I]. The total amount of upgrades stays the same, the total cost is cheaper, which means this new plan is definitely more optimal.
Now, combining Observation 3.2 with Observation 3.3, we can make the following observation:
Observation 4: Even if we straight up stop caring about the relative position of all cities, and start considering each city as a respective item that has a certain cost to upgrade to Lv1 and Lv2, there would always exist a solution with the optimal amount of upgrades that satisfies the original constraint (City I is only reachable from X if the budget spent on city I is larger than DistX[I], and every single city on the XI — path must also be reachable from X) anyways.
With this observation in mind, the lengthy problem statement can be turned into something like this: "There are N bags, each contains 2 items. For bag i, you could pay Cost1[i] coins to take 1 item from bag i, or pay Cost1[i]+Cost2[i] coins to take 2 items from bag i. For some bags, you must take at least 1 item. You have K coins, find the largest amount of items you could buy", which is......a standard knapsack DP problem. Seriously.
At this point, we just let DP[i][j] be the minimum amount of coins needed to buy exactly j items from the first i bags. The DP transition is now obvious and trivial. (To be honest, this might be the first time I've ever seen a problem go "We added this restriction in but it basically could be completely ignored, just screw it and DP, lmao). This task is very cool, cute and funny. Definitely among the more interesting DP task I've seen so far.
With the "basic DP formula that you could come up in 5 minutes after making some observations or maybe even just guessing randomly", you have already obtained 75 points. Very funny. If you know how to BFS/DFS and know how to implement the basic DP Knapsack thing, you've already secured yourself 75 points with less than 50 lines of code or something, weird. If you are an IOI participant, you should know how to implement BFS/DFS and a basic 2D DP, right? Right????
Exactly 29 contestant has a score higher than 73, in contest, for this task. Not adding hints for this task is a mistake (kind of).
Time complexity: O(N * 2N)
Part 4: What would you get from doing something nobody asked for? 75% of the full solution (Subtask 4.5)
From Observation 4, we can see that there obviously exists a greedy NlogN solution that uses some data structure that could keep track of the cheapest availible upgrade and do stuffs. Yes, I'm talking about priority queues.
Let's look at the constrains about upgrades we've figured out so far:
Upgrading a city from Lv0 to Lv1 could be done at any time, without any further restrictions
Upgrading a city i from Lv1 to Lv2 requires the upgrade that brings city i from Lv0 to Lv1 must be made beforehand.
Intuitively, we could do the following:
1) Consider the case where the level cap to all cities is 1 seperately — like we've done for the other 5-6 subtasks or something
2) Upgrade all cities on the XY — path to Lv1, reduce the budget accordingly. Upgrading cities that lies on the XY — path to Lv2 is now available.
3) Try to just push every single currently available upgrades into a priority queue. That is, all upgrades that brings a city i that doesn't lie on the XY — path to Lv1, and upgrades that brings cities lying on the XY — path to Lv2.
4) We now pick the cheapest availible upgrade, do it, and then pay the cost. Once a city is upgraded to Lv1, upgrading it to Lv2 is now possible, so we now push this upgrade into the priority queue. We can keep track of the amount of upgrades made to city i by using an additional array check[i]. Adjust the remaining budget accordingly.
5) Repeat until we can't do that anymore.
(My implementation: solution that somehow works (ignore the Vietnamese texts, it's just there so that my code looks like less of a mess. No comment needed — it's simple enough)
If you try that and submit it blindly, you will somehow pass subtask 2,3 and 4. So it does work for the lines subtasks, after all. But why only the line subtasks, and not, you know, everything? As it turns out, it actually doesn't just work with the line subtasks, but with tests where the path from X to Y doesn't have any additional branch as well (that is, for all cities L that belongs on the XY path and is not X or Y, L is adjacent to exactly 2 cities). Here's why.
First, we'll have to determine what could possibly mess the intuitive solution up.
The cities that could break our seemingly reasonable greedy approach are those with very high Cost1, but low Cost2. For example, let's consider those 2 cities:
1) XY = 10. M is the midpoint of XY. Cost1[M]=5, Cost2[M]=0
2) O is an unbounded city. OX = 2. Cost1[O]=2, Cost2[O]=10
If we only have 5 coins left, choosing to upgrade city M to Lv1, then get a free Lv2 is more beneficial than upgrading city O to Lv1 and then stop everything. The cities O that will kill our greedy algorithm are those with Cost1[O] > Cost2[O], in the general tree case. However, when there are no cities branching out from the path between X and Y, the process of picking cities to upgrade would be divided into 3 phases that would still yield a correct answer like this:
- Phase 1: Doing all upgrades with cost < DistX[Y]. In this phase, cities O with both upgrades having a cost < DistX[Y] AND Cost1[O] > Cost2[O] are all bounded cities — which happens to lie on the XY path. As we've been forced to upgrade them to Lv1 before the greedy process even started, they are now unable to break our greedy algorithm.
- Phase 2: Now, for cities O with Cost1[O] > DistX[Y], all such cities aren't bounded, and Cost2[O] would be DistX[Y] (see observation 3.1). When we upgrade the city with cheapest Cost1 and unlock the option to upgrade that city to Lv2, that upgrade will be made immediately, before picking yet another un-upgraded city to bring to Lv1. This is obvious: For all cities not picked so far, their Cost1 is all > DistX[Y], while their Cost2 is exactly DistX[Y], so immediately bringing them to Lv2 is always more optimal than bringing an un-upgraded city to Lv1.
=> In the case where the path between X and Y has no branches, the greedy solution above would still always make the optimal choice at each step, since all points that could possibly mess it up is...already picked by default. Very cool and funny (2).
Also, if you're paying attention, in this case, once the greedy process has entered Phase 2, it would end immediately the moment a city can no longer be upgraded from Lv1 to Lv2 or there is no more city to upgrade, which means that there would be 1 city that would end up at Lv1. Hmm, I wonder if that would turn out to be the crucial observation for the full solution of this task.
Time complexity: O(N log N), but only correct for cases where all "bounded" cities are on the path between x and Y
Part 5: The full solution
So, our previous greedy algorithm is having problems when there are cities O with Cost1[O] > Cost2[O] and aren't picked by default exists. When we encounter something that breaks our algorithm completely, what should we do? Abandon our solution immediately, looking for an alternative, or trying to come up with a way to consider the edge cases seperately for 15 minutes or so? Obviously the latter.
We now categorize cities by its type. A city i will have
Type 0 if it's just a normal city — no special features.
Type 1 if Cost1[i] > Cost2[i]
Type 2 if i is on the path between X and Y (or Cost1[i]*2 + Cost2[i] == DistX[Y])
After analyzing how the "wrong" greedy algorithm still manages to work out as above, we start to notice something: For some reason, all cities but one in phase 2 are either maxxed out (brought to Lv2), or not touched at all, and there's at most 1 city that could end up at Lv1 once Phase 2 has been initiated. Would that be the case here? Turns out, it is!
Observation 5: For all but one Type 1 cities, we will either ignore them, or max them out.
Proof: Consider the moment we started picking the first Type 1 city (call it O, again). Similarly to all previous subtasks, this is the one with the lowest Cost1. At that point:
If there exists 2 upgrade with cost < Cost1[O] to a Type 0/2 city and we don't want to upgrade this city to Lv2, we would just pick both of those instead of upgrading city O to Lv1 at all.
If there is only 1 cheaper upgrade to a Type 0/2 city and we don't want to upgrade this city to Lv2, there are no available, cheaper upgrade than upgrading O to Lv2 after we've done this final upgrade. We could come to this state with some budget left — which makes the answer unoptimal.
If there is no more upgrade to a Type 0/2 city possible OR we don't have enough budget to pay for upgrading city O to Lv2, there is nothing else we can do — every upgrade currently availible either costs more than just simply upgrading city O to Lv2, or cost more than our remaining budget.
From the proof above, it's already clear which steps our algorithm have to make:
- Step 1: Using BFS/DFS to calculate Cost1[i] and Cost2[i] for all cities i
- Step 2: Assume that all cities has a level cap of 1. Find the optimal answer in this case — Ans1 using priority queue
- Step 3: Start considering the case where the level cap for all cities is 2. Greedily pick the upgrades in 3 phases:
1) Phase 1 — Preparation: Upgrade all Type 2 cities to Lv1, pushing the upgrades that brings Type 2 cities to Lv2 into the first priority queue. Push the cost of upgrades to Type 0 cities into the first priority queue as well. Push the cost of maxxing out each Type 1 cities into the second Priority Queue. The 3rd Priority Queue is for deciding whether to upgrade a Type 1 city to Lv1 at the end or not. Push Cost1 of all Type 1 cities into the 3rd priority queue.
2) Phase 2 — Execution: Constantly compare the most optimal option at the moment: Maxxing out the cheapest Type 1 city currently available and increase the total amount of levels by 2, or pick the cheapest remaining upgrade in the 1st priority queue. If the total cost of making the 2 cheapest upgrade currently possible in the first priority queue is more than the cost to fully upgrade the cheapest Type 1 city currently possible, do the cheapest upgrade in pq1, remove it from the prioritu queue, and then compare again.
3) Phase 3 — Endgame: Picking the remaining upgrades in 1st priority queue, removing picked upgrades until there is nothing left or the budget is no longer sufficient. If the upgrade to that one Type 1 city that has the cheapest Cost 1 could still be made, do it.
- Step 4: Compare the current answer to Ans1. The larger of the two is the answer to the problem.
Time Complexity: O(NlogN)
My submission (it is actually shorter than 1/10 of this post, and has explaination as well): 233 lines, nice
Additional things that you can do:
As everything is pushed into vectors at the start, you could use 3 different vectors and sort them beforehand for a slightly faster runtime, then use 2-pointers. I decided against it as it isn't as easy to understand and anywhere nearly as intuitive as using priority queues.
==================
My opinion about the task:
Good points:
Very fun and rewarding task — if there is at least 5 different ways to do the task, it's good in my book (I know there's a solution using Fenwick Trees or something like that to speed up subtask 8's DP solution as well, but it doesn't seem as "clean" as the greedy solution with 3 priority queues to me). Each observation actually contributes a lot to reaching the final solution.
The O(N^2) DP solution, while borderline braindead, is pretty interesting (obviously nowhere nearly as wacky and weird and unusual as P3 but still very interesting — "Just find the optimal decisions, it'll satisfy the other conditions by itself" is something I haven't seen before, ever)
Actually around as good as POI tree tasks, wow.
2 different paths (that I know of) to the full solution, with balanced difficulty for both. Wow. That's....very impressive
"Questionable" points:
Who tf would realistically, unironically care about "sum of all closing times"?????? Making it some limited variable that people actually cares about (time travelled, money) would be a little bit less unrealisticly hilarious (still better than "You're given an array as a birthday gift though)
There isn't a subtask 4.5 in the actual task. If there actually were a subtask where the tree is a line, N <= 200000, it would have been much better: Contestant won't have to come up with some dark magic O(N^2) solution for lines instead of the far simplier NlogN greedy solution, they could also come up with the full solution from improvising the NlogN line solution
The O(N^2) DP solution is far too cheap — 75 pts for some intuition/ a single observation, while getting to 100pts requires 4 additional observations or 200 additional lines of segment trees is probably not that fair. I think that changing the constrains for N in subtask 4 from N <= 3000 to N <= 200000, or add a subtask where N <= 200000 and the path between X and Y has no additional branches (serving as a hint for "considering cities where Cost1[i]> Cost2[i] seperately") would both make the DP solution less unfairly free and coming up with the full greedy solution easier.
The scoring for this task is incredibly off:
1) A DP solution that requires exactly 1 observation (that took me 5 minutes to discover) and basic DP knowledge gives 83 points. It's essentially giving free points — far too much compared to what it should have.
2) A greedy solution that could be easily improved into a full solution gets 43 points, requires 3 observations, and....doesn't even exist in the task (I still can't understand why wouldn't the ISC add the N<=200000 subtask, considering the fact that, to me (and probably at least 20 other contestant. Not that I am one), the NlogN solution is much easier to come up with compared to the N^3 and N^2 solution. Heck, even until today I still don't know what could possibly solve only subtask 2,3,4, with a complexity of N^2, and nothing else.
3) The path to the full solution is extremely off. We have 2 paths here: Improvising the DP solution by chucking in 100+ lines of trees for 17 points (not worth it for contestants? — at least that's what I heard from the Vietnamese team), or improving from a subtask that should've existed, but didn't for 57 points (more balanced, but this much of a leap is just...what? Even Combo/Molecules has a less steep scoring distribution — and those were supposed to be "easy" tasks. It is still balanced in a way, perhaps even being a good thing though: either you take the easier path to 83pts and spend the next hour chugging 600 lines of data structures for 17 point, or taking the harder path and improvising from something nobody asked for to get a relatively clean solution.










