Physics has many cheating statements, like conservation laws, which can help to "prove" interesting math facts. If you know any "proofs", you can share them. I also know some:
Tetrahedron normals
Pythagorean theorem
Точка Торричелли
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3690 |
| 2 | jiangly | 3647 |
| 3 | Benq | 3581 |
| 4 | orzdevinwang | 3570 |
| 5 | Geothermal | 3569 |
| 5 | cnnfls_csy | 3569 |
| 7 | Radewoosh | 3509 |
| 8 | ecnerwala | 3486 |
| 9 | jqdai0815 | 3474 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 165 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 160 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | orz | 146 |
| 9 | pajenegod | 145 |
| 9 | SecondThread | 145 |
Physics has many cheating statements, like conservation laws, which can help to "prove" interesting math facts. If you know any "proofs", you can share them. I also know some:
Tetrahedron normals
In a tetrahedron, external normal vectors are drawn to all faces. The length of each vector is numerically equal to the area of the corresponding face. Prove that the sum of vectors is 0
Let us pump gas at pressure p into the tetrahedron. Then the force the gas pushes on the face is perpendicular to the face and proportional to its area: F = pS. From the equilibrium condition, the sum of the forces is 0, and then the sum of our vectors is also 0. This proof can easily be generalized to an arbitrary polyhedron.
Pythagorean theorem
Well-known
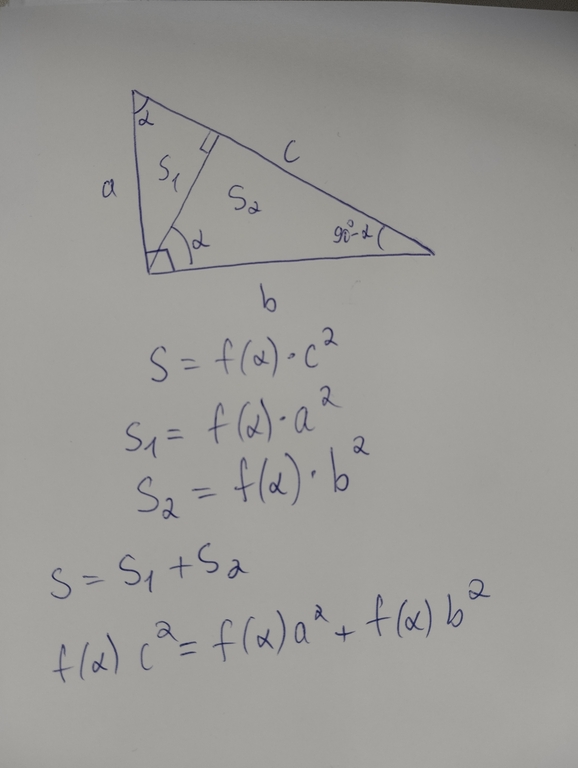
A right triangle is defined by the hypotenuse c and the vertex angle α. Then, from dimensional considerations, its area S is equal to f(α) * c^2, where f(x) — some function of the angle (in fact, f(x) = 0.5 * sin(x)). Let's draw the height to the hypotenuse, dividing the triangle into two small triangles with areas S1 and S2. Both triangles have an angle α. Summing up their areas using the formula, we reduce them by f(α) and get the equality.
Точка Торричелли
Inside an acute triangle ABC, a point P is marked, minimizing the sum of the distances PA+PB+PC. Prove that the sides of the triangle ABC are visible from point P at equal angles.

Let's fasten three threads at one point (point P), which can slide freely along the plane. Let's make holes in the vertices of the triangle and pass the threads through them. We attach 3 equal masses on the lower ends of the threads. The minimum potential energy corresponds to the maximum total length of the vertical segments of the threads, that is, the minimum total length of segments PA, PB, PC. Point P is in a state of equilibrium, and three identical forces pull it. Then, from symmetry, the angles between each pair of threads are equal to 120 degrees.
(Unfortunately, Codeforces does not support emoji, so it is here)
Hello, Codeforces. I wrote a prorgam using this theorem for interpolation a function as a polynomial. At first, I will explain how does it work and then show some examples of using it.
Wikipedia does not provide one formula I need, so I will show it
If there are now monomials with all exponents more or equal than our exponents, the coefficient with our monomial can be calculated by formula 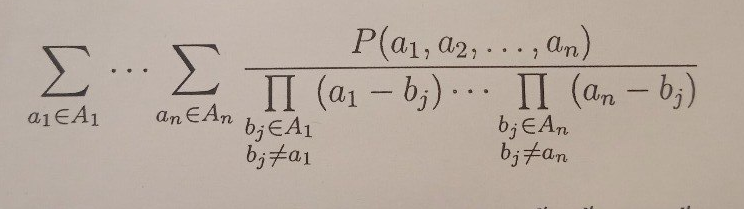
Code is quite long, but simple in use.
At first, you need to set values of constants. N is the number of variables, MAX_DEG is the maximal exponent of a variable over all monomials. In main you need to fill 2 arrays: names contains the names of all variables, max_exp[i] is the maximal exponent of the i-th variable, or the upper_bound of its value.
Define d = (max_exp[0] + 1) * (max_exp[1] + 1) * ... * (max_exp[N - 1] + 1). MAX_PRODUCT should be greater then d. Then you need to write a function f(array<ll, N>), which returns ll or ld. In my code it returns an integer, but its type is ld to avoid ll overflow.
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define fi first
#define se second
#define pb push_back
#define cok cout << (ok ? "YES\n" : "NO\n");
#define dbg(x) cout << (#x) << ": " << (x) << endl;
#define dbga(x,l,r) cout << (#x) << ": "; for (int ii=l;ii<r;ii++) cout << x[ii] << " "; cout << endl;
// #define int long long
#define pi pair<int, int>
const int N = 7, C = 1e7, MAX_DEG = 4, MAX_PRODUCT = 1e5;
const ld EPS = 1e-9, EPS_CHECK = 1e-9;
const string SEP = " (", END = ")\n";
const bool APPROXIMATION = true;
array <string, N> names;
array <int, N> max_exp, powers, current_converted, cur_exp;
array<vector<ll>, N> POINTS;
ll DIV[N][MAX_DEG + 1][MAX_DEG + 1], PW[N][MAX_DEG + 1][MAX_DEG + 1];
ld SUM[MAX_PRODUCT];
ld F_CACHE[MAX_PRODUCT];
ll pow(ll a, int b)
{
if (b == 0) return 1;
if (b == 1) return a;
ll s = pow(a, b / 2);
s *= s;
if (b & 1) s *= a;
return s;
}
ld approximate(ld k)
{
int k_ = k;
int k__ = k_ + abs(k) / k;
if (abs(k - k_) < EPS) return k_;
else if (abs(k - k__) < EPS) return k__;
else
{
int i = 1, j = 1;
ld ka = abs(k);
while (i < C && j < C)
{
ld p = ka * j;
if (abs(p - i) < EPS) break;
if (p < i) j++;
else i++;
}
if (i >= C || j >= C) return k;
if (k < 0) i = -i;
return (ld)i / j;
}
}
void normalize(ld k)
{
if (!APPROXIMATION)
{
cout << k << SEP;
return;
}
int k_ = k;
int k__ = k_ + abs(k) / k;
if (abs(k - k_) < EPS) cout << k_ << SEP;
else if (abs(k - k__) < EPS) cout << k__ << SEP;
else
{
int i = 1, j = 1;
ld ka = abs(k);
while (i < C && j < C)
{
ld p = ka * j;
if (abs(p - i) < EPS) break;
if (p < i) j++;
else i++;
}
if (i >= C || j >= C)
{
cout << k << SEP;
return;
}
if (k < 0) i = -i;
cout << i << "/" << j << SEP;
}
}
struct monom
{
array<int, N> exp;
ld k;
int deg;
monom(array<int, N> v, ld k_)
{
k = k_;
exp = v;
deg = 0;
for (int i=0;i<N;i++) deg += exp[i];
}
void display()
{
normalize(k);
if (deg == 0) { cout << "1" << END; return;}
bool go = 0;
for (int i=0;i<N;i++)
{
if (go && exp[i]) cout << " * ";
if (exp[i]) go = 1, cout << names[i] + "^" + to_string(exp[i]);
}
cout << END;
}
ld operator()(array<int, N> v)
{
ll res = 1;
for (int i=0;i<N;i++) res *= PW[i][v[i]][exp[i]];
return k * res;
}
ld getRandom(array<ll, N> v)
{
ld res = 1;
for (int i=0;i<N;i++) res *= pow(v[i], exp[i]);
return k * res;
}
};
bool operator<(monom a, monom b)
{
if (a.deg > b.deg) return 1;
if (a.deg < b.deg) return 0;
if (a.exp > b.exp) return 1;
if (a.exp < b.exp) return 0;
return a.k > b.k;
}
struct polynom
{
vector<monom> st;
void add(monom m)
{
if (abs(m.k) < EPS) return;
st.pb(m);
}
void print() { if(st.size() == 0) {cout << "Polynom is 0\n"; return;} sort(st.begin(), st.end()); for (monom &m: st) m.display();}
ld operator()(array<ll, N> v)
{
ld res = 0;
for (auto &m: st) res += m.getRandom(v);
return res;
}
};
ld gen(int index=0, int current_hash=0)
{
if (index == N)
{
ll div = 1;
for (int i=0;i<N;i++) div *= DIV[i][current_converted[i]][cur_exp[i]];
return (ld)(F_CACHE[current_hash] - SUM[current_hash]) / div;
}
ld res = 0;
for (int i=0;i<=cur_exp[index];i++)
{
current_converted[index] = i;
res += gen(index + 1, current_hash + i * powers[index]);
}
return res;
}
array<int, N> convert(int h)
{
array<int, N> res;
for (int i=0;i<N;i++) res[i] = h / powers[i], h -= res[i] * powers[i];
return res;
}
array<ll, N> convert_points(int h)
{
array<ll, N> res;
for (int i=0;i<N;i++) res[i] = POINTS[i][h / powers[i]], h %= powers[i];
return res;
}
polynom interpolate(ld f(array<ll, N>))
{
int max_pow = -2e9, sum = 0, h_max = 0;
set<int> remaining_points, st;
polynom res;
for (int x: max_exp) max_pow = max(max_pow, x), sum += x, h_max = h_max * (x + 1) + x;
powers[N - 1] = 1;
for (int i=N-2;i>-1;i--) powers[i] = powers[i + 1] * (max_exp[i + 1] + 1);
for (int i=0;i<max_exp.size();i++) for (int j=0;j<=max_exp[i];j++) POINTS[i].pb(j);
for (int i=0;i<N;i++) for (int j=0;j<=max_exp[i];j++) for (int u=0;u<=max_exp[i];u++) DIV[i][j][u] = (u ? DIV[i][j][u - 1] : 1) * (u == j ? 1 : (POINTS[i][j] - POINTS[i][u]));
for (int i=0;i<N;i++) for (int j=0;j<=max_exp[i];j++) for (int u=0;u<=max_pow;u++) PW[i][j][u] = u ? PW[i][j][u - 1] * POINTS[i][j] : 1;
for (int i=0;i<=h_max;i++) F_CACHE[i] = f(convert_points(i)), remaining_points.insert(i);
st.insert(h_max);
while (st.size())
{
int v = *st.rbegin();
st.erase(v);
remaining_points.erase(v);
cur_exp = convert(v);
ld k = gen();
if (abs(k) > EPS)
{
if (APPROXIMATION) k = approximate(k);
monom mn = monom(cur_exp, k);
res.add(mn);
for (int i: remaining_points) SUM[i] += mn(convert(i));
}
for (int i=0;i<N;i++) if (cur_exp[i]) st.insert(v - powers[i]);
}
return res;
}
ld f(array<ll, N> v)
{
auto [a, b, c, d, e, f, g] = v;
ld res = 0;
for (int i=0;i<a;i++)
for (int j=0;j<b;j++)
for (int u=0;u<c;u++)
for (int x=0;x<d;x++)
for (int y=0;y<e;y++)
for (int z=0;z<f;z++)
for (int k=0;k<g;k++)
res += 13ll * i * j * u * i * i * u - 49ll * k * k * z * z * y + 90ll * c * u * k * x * x * x;
return res;
}
void check(polynom p, ld(array<ll, N> f))
{
mt19937 rnd(228);
for (int i=0;i<10000;i++)
{
int t = clock();
array<ll, N> ex;
for (int j=0;j<N;j++) ex[j] = rnd() % 20 + 2;
ld F = f(ex);
ld P = p(ex);
if (abs(F - P) > max(EPS_CHECK, EPS_CHECK * abs(F)))
{
cout << "Polynom is wrong, test " << i << endl;
cout << F << endl << P << endl;
for (int x: ex) cout << x << " ";
cout << endl;
return;
}
cout << "Test " << i << " has been passed, time = " << (ld)(clock() - t) / CLOCKS_PER_SEC << "s" << endl;
}
cout << "Polynom is OK" << endl;
}
signed main()
{
cin.tie(0); ios_base::sync_with_stdio(0);
cout << setprecision(20) << fixed;
names = {"a", "b", "c", "d", "e", "f", "g"};
max_exp = {4, 2, 3, 4, 2, 3, 3};
polynom P = interpolate(f);
P.print();
//cout << "Checking polynom..." << endl;
//check(P, f);
}
If you uncomment 2 last rows in main, program will check the polynom it got on random tests. The test generation should depend from f working time, because it can run too long on big tests.
Function from exaple and similar functions (with n loops) are a polynomial with rational coefficients (if this is not true, the function does not return an integer). So, if APPROXIMATION = true, all coefficients are approximating to rational numbers with absolute error < EPS with functions normalize and approximate (they are using the same algorithm). This algorithm works in O(numerator + denominator), that seems to be slow, but if the polynomial has a small amount of monomials, it does not take much time.
Stress-testing function check considers a value correct if its absolute or relative error < EPS_CHECK.
We consider monomials as arrays of exponents. We hash these arrays. Array PW contains powers of points (from POINTS), which we use for interpolation. If you want to use your points for interpolation, modify POINTS. If you use fractional numbers, replace #define ll long long with #define ll long double. Array DIV is used for fast calculating denominators in the formula.
convert(h) — get indexes (in array POINTS) of coordinates of the point corresponding to the monomial with hash h. convert_points(h) — get coordinates of the point corresponding to the monomial with hash h.
Then we are precalcing values of f in all our points and write them to F_CACHE. After it, we run bfs on monomials. During the transition from one monomial to another we decrease the exponent of one variable by 1. When a monomial is got from set in bfs, we find its coefficient using gen. If it is not zero, we need to modify our polynomial for every monomials we has not considered in bfs yet ("monomial" and "point" have the same concepts because we can get a point from monomial using convert_points(h), if h is a hash of the monomial).
We need to modify the polynomial to make one of the theorem's conditions satisfied: there are no monomials greater than our monomial (greater means that all exponents are more or equal). For every point we has not consider in bfs (they will be in set remaining_points) we add the value of the monomial in this point to SUM[hash_of_point]. Then we will decrease f(point) by SUM[hash_of_point] to artificially remove greater monomials.
gen is iterating over O(d) points, denominator calculation takes O(N) time for each point.We have got O(d * O(f) + d^2 * N + d * O(res)), where O(res) is the time it takes to calculate the polynomial we got as a result.
It seems that the recursion takes the most time. We can unroll it in one cycle using stack. It is boring, so I decided to try to unroll it in other way. For every monomial with non-zero coefficient, let`s iterate over all monomials with hash less or equal to our hash. For every monomial we check if it is less than our monomial (all corresponding exponents are less or equal). If it is lower, we add to the coefficient the value of fraction in this point (monomial).
// Instead of ld k = gen();
ld k = 0;
for (int h=0;h<=v;h++)
{
array<int, N> cur = convert(h);
bool ok = 1;
for (int i=0;i<N;i++) if (cur[i] > cur_exp[i]) ok = 0;
if (ok)
{
ll div = 1;
for (int i=0;i<N;i++) div *= DIV[i][cur[i]][cur_exp[i]];
k += (ld)(F_CACHE[h] - SUM[h]) / div;
}
}
Is it faster than gen? New implementation is iterating over all pairs of hashes, so it works in O(d^2 * N), too. Let's estimate the constant. The number of these pairs is d * (d + 1) / 2, so we get constant 1 / 2. Now let's calculate the constant of number of points considered by gen. This number can be calculated with this function:
ld f(array<ll, N> v)
{
auto [a, b, c, d, e, f, g] = v;
ld res = 0;
for (int i=0;i<a;i++)
for (int j=0;j<b;j++)
for (int u=0;u<c;u++)
for (int x=0;x<d;x++)
for (int y=0;y<e;y++)
for (int z=0;z<f;z++)
for (int k=0;k<g;k++)
res += (i + 1) * (j + 1) * (u + 1) * (x + 1) * (y + 1) * (z + 1) * (k + 1);
return res;
}
The coefficient with a^2 * b^2 * c^2 * d^2 * e^2 * f^2 is our constant. To find it, I used my program. It is 1 / 128. At all, it is 1 / 2^N for N variables. It means that the optimization can be efficient if N is small.
May be, this program will help someone to find formula for some function. Also it can open brackets, that is necessary if you calculate geometry problems in complex numbers. If you know other ways to use it, I will be happy if you share it.
With N = 1 this program is just a Lagrange interpolation, which can be done faster than O(d^2). Maybe, someone will find a way to speed up it with N > 1.
Hello, Codeforces. I submitted two very similar solutions to 1771F - Hossam and Range Minimum Query
You can see that they are different in one line with map. I have no idea why the first solution gets TL.
Hello, Codeforces. Recently I invented a problem. Consider a set of points (x, y) with integer coordinates, 0 <= x < a и 0 <= y < b. We want to know the number of acute triangles with vertices at given points.
We can write function f(a, b) which finds the answer and works in (ab) ^ 3. I suggested that it is a polynomial of two variables with degree <= 6. I tried to interpolate it using this theorem. But my code finds non-zero coefficients with monoms with degrees > 6, so my hypothesis was not confirmed. I also failed with right triangles.
int stupid(int a, int b)
{
int ans = 0;
for (int x1=0;x1<a;x1++)
for (int x2=0;x2<a;x2++)
for (int x3=0;x3<a;x3++)
for (int y1=0;y1<b;y1++)
for (int y2=0;y2<b;y2++)
for (int y3=0;y3<b;y3++)
{
int a = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
int b = (x1 - x3) * (x1 - x3) + (y1 - y3) * (y1 - y3);
int c = (x3 - x2) * (x3 - x2) + (y3 - y2) * (y3 - y2);
if ((a + b == c) && min(a, min(b, c))) ans++;
}
return ans / 2;
}
signed main()
{
int C1 = 5, C2 = 5;
ld res = 0;
for (int a1=4;a1<=C1+3;a1++)
{
for (int a2=4;a2<=C2+3;a2++)
{
int d = 1;
for (int ai=4;ai<=C1+3;ai++) if (ai != a1) d *= a1 - ai;
for (int ai=4;ai<=C2+3;ai++) if (ai != a2) d *= a2 - ai;
res += (ld)(stupid(a1, a2)) / d;
}
}
cout << setprecision(20) << fixed << res;
}
This code finds a coefficient with a ^ (C1 - 1) * b ^ (C2 - 1)
UPD: Found formula for the number of right triangles with b = 2: f(a, 2) = 2 * a ^ 2 - 4, a > 1.
UPD2: Many thanks to bronze_coder for finding O(1) solution for constant b: OEIS A189814.
Interpolation should use ai > b ^ 2.
UPD3: Finally wrote a O((ab) ^ 2) solution.
int fast(int a, int b)
{
int ans = 0;
for (int a1=-a+1;a1<=a-1;a1++)
{
for (int b1=-b+1;b1<=b-1;b1++)
{
if (a1 == 0 && b1 == 0) continue;
for (int a2=-a+1;a2<=a-1;a2++)
{
for (int b2=-b+1;b2<=b-1;b2++)
{
if (a2 == 0 && b2 == 0) continue;
// first condition is that dot product = 0
// second condition is that cross product < 0 not to count the same pair twice
if (b1 * b2 + a1 * a2 == 0 && a1 * b2 - b1 * a2 < 0)
{
int cnta = a - max(max(abs(a1), abs(a2)), abs(a1 - a2));
int cntb = b - max(max(abs(b1), abs(b2)), abs(b1 - b2));
if (cnta > 0 && cntb > 0) ans += cnta * cntb;
}
}
}
}
}
return ans;
}
Now I can interpolate using bigger values of a and b.
But it is quite strange for me that the number of right triangles is directly proportional to (ab) ^ 2 instead of (ab) ^ 3. Now I will try to understand why the formula doesn't work with ai <= b ^ 2.
UPD4: Code that finds a formula for f(a, b) for a > b ^ 2 and works in O(b ^ 6):
int fast(int a, int b)
{
int ans = 0;
for (int a1=-a+1;a1<=a-1;a1++)
for (int b1=-b+1;b1<=b-1;b1++)
{
if (a1 == 0 && b1 == 0) continue;
for (int a2=-a+1;a2<=a-1;a2++)
for (int b2=-b+1;b2<=b-1;b2++)
{
if (a2 == 0 && b2 == 0) continue;
if (b1 * b2 + a1 * a2 == 0 && a1 * b2 - b1 * a2 < 0)
{
int cnta = a - max(max(abs(a1), abs(a2)), abs(a1 - a2));
int cntb = b - max(max(abs(b1), abs(b2)), abs(b1 - b2));
if (cnta > 0 && cntb > 0) ans += cnta * cntb;
}
}
}
return ans;
}
struct polynom
{
int x0 = 0, x1 = 0, x2 = 0;
void print()
{
cout << x2 << "x^2 + " << x1 << "x - " << -x0 << endl;
}
ld get(ld x)
{
return x2 * x * x + x1 * x + x0;
}
};
void interpolate(int b)
{
polynom P = {0, 0, 0};
vector<int> A = {b * b + 1, b * b + 2, b * b + 3};
ld res = 0;
vector<ld> B = {fast(A[0], b), fast(A[1], b), fast(A[2], b)};
for (int i=0;i<3;i++)
{
int d = 1;
for (int j=0;j<3;j++) if (A[i] != A[j]) d *= A[i] - A[j];
res += (B[i] - P.get(A[i])) / d;
}
P.x2 = res;
res = 0;
A.pop_back();
for (int i=0;i<2;i++)
{
int d = 1;
for (int j=0;j<2;j++) if (A[i] != A[j]) d *= A[i] - A[j];
res += (B[i] - P.get(A[i])) / d;
}
P.x1 = res;
P.x0 = B[0] - P.get(A[0]);
P.print();
}
I used OEIS to find a regularity between the coefficients of P, but i didn't find anything :( except x2 = b * (b - 1), but it was obvious.
UPD5:
O(min(a, b) ^ 6)If a < b, let's swap them. Now we need to solve it in O(b ^ 6). If a <= (b - 1) ^ 2 + 1, we can run solution in O((ab) ^ 3) = O(b ^ 6). Now we need to solve it for a > (b - 1) ^ 2 + 1.
Consider all right triangles and divide them into 3 types:
triangles without any vertices on the line x = a - 1
triangles with some vertices on the line x = a - 1 and with two sides which are parallel to the x-axis or y-axis
other triangles
Let C(a) be the number of third type triangles (some function).
The number of second type triangles is (a - 1) * b * (b - 1) / 2 * 4:
Let's choose a vertical line x = z, z < a - 1 (a - 1 variants), a vertical line x = a - 1 and two horizontal lines (b * (b - 1) / 2 variants). Intersection of these lines consists of 4 points. We can throw away any of them and the triangle formed from other 3 points has the second type. Obviously, every second type triangle can be presented as an intersection of these lines without one of points.
By definition, for every vertex (x, y) of first type triangles, 0 <= x < a - 1 and 0 <= y < b, then the number of the triangles is f(a - 1, b), by definition of f.
Well, f(a, b) = f(a - 1, b) + (a - 1) * b * (b - 1) / 2 * 4 + C(a)
Let's prove that C(a) for every a > (b - 1) ^ 2 + 1 has same values.
Lemma. Maximal absolute value of difference between abscissas of two vertices of a third type triangle does not exceed (b - 1) ^ 2 + 1
Let's look on a picture
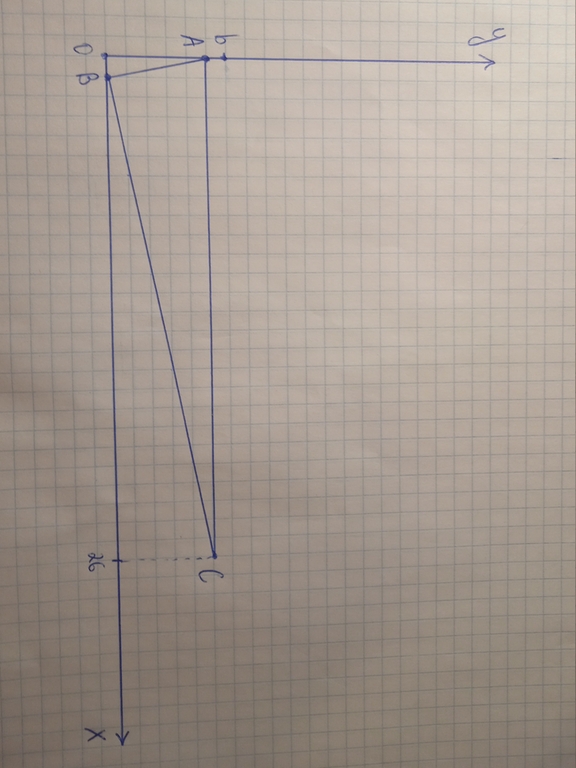
The triangle has at least two sides which are parallel to neither x-axis nor y-axis (AB and BC). Let k be the slope of line AB, then the slope of BC is equal to -1/k. Then, the difference between abscissas of A and C does not exceed
(b - 1) / |k| + (b - 1) / |-1/k| = (b - 1) * (|k| + 1 / |k|).
It is a well-known fact that if we have two positive numbers and we will bring their values together and their product remains the same, then their sum will decrease. Then, to maximize |k| + 1 / |k|, we need minimize or maximize |k|. According to limitation of coordinates, |k| < b - 1 and 1 / |k| < b - 1. Then the maximum value is (b - 1) * ((b - 1) + 1 / (b - 1)) = (b - 1) ^ 2 + 1. The Lemma is proved.
We need to prove that for a > (b - 1) ^ 2 + 1 the number of third type triangles does not depend on a. It is obvious after proving Lemma because we can compare every triangle for a with a triangle for a + 1 by shifting it to right.
C(a) is a constant. Let c be this constant.
Well, f(a, b) = f(a - 1, b) + (a - 1) * b * (b - 1) / 2 * 4 + c. After some transforms, we get a formula for f(a, b) using f((b - 1) ^ 2 + 1, b).

ll fast(int a, int b)
{
ll ans = 0;
for (int a1=-a+1;a1<=a-1;a1++)
for (int b1=-b+1;b1<=b-1;b1++)
{
if (a1 == 0 && b1 == 0) continue;
for (int a2=-a+1;a2<=a-1;a2++)
for (int b2=-b+1;b2<=b-1;b2++)
{
if (a2 == 0 && b2 == 0) continue;
if (b1 * b2 + a1 * a2 == 0 && a1 * b2 - b1 * a2 < 0)
{
int cnta = a - max(max(abs(a1), abs(a2)), abs(a1 - a2));
int cntb = b - max(max(abs(b1), abs(b2)), abs(b1 - b2));
if (cnta > 0 && cntb > 0) ans += cnta * cntb;
}
}
}
return ans;
}
struct polynom
{
ll x0 = 0, x1 = 0, x2 = 0;
void print()
{
cout << x2 << "x^2 + " << x1 << "x - " << -x0 << endl;
}
ld get(ld x)
{
return x2 * x * x + x1 * x + x0;
}
};
ll get(int a, int b)
{
if (a < b) swap(a, b);
if (a <= (b - 1) * (b - 1) + 1) return fast(a, b);
int x = fast((b - 1) * (b - 1) + 1, b);
int y = fast((b - 1) * (b - 1) + 2, b);
// y = x + c + (a - 1) * b * (b - 1) / 2 * 4;
int c = y - x - ((b - 1) * (b - 1) + 1) * (b - 1) * b * 2;
polynom P;
P.x2 = b * b - b;
P.x1 = c - b * b + b;
P.x0 =-b*b*b*b*b*b + 5*b*b*b*b*b - 11*b*b*b*b + 13*b*b*b + b*b*(-8 - c) + b * (2 * c + 2) - 2 * c + x;
return P.get(a);
}
Unfortunately, the value of c is different for different values of b and I could not find a regularity between them. Interpolation and OEIS did not help me. There are some things I should do:
c through b, after all c depends on b onlya <= (b - 1) ^ 2 fasterIt will be hard.
UPD6: We can speed up the solution to O(b^5) using this idea
| Name |
|---|


