Physics has many cheating statements, like conservation laws, which can help to "prove" interesting math facts. If you know any "proofs", you can share them. I also know some:
Tetrahedron normals
Statement
Solution
Pythagorean theorem
Statement
Solution
Точка Торричелли
Statement
Solution



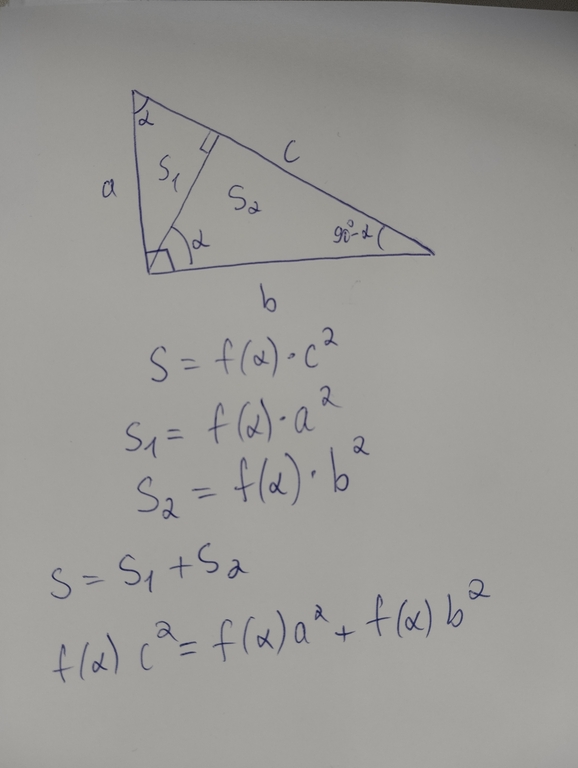








Auto comment: topic has been translated by polosatic (original revision, translated revision, compare)
I liked how you used $$$\mathtt{Phsysics}$$$ as non-math based , and make it like the base of $$$\mathtt{Math}$$$
Altought it's vice versa.
Interesting topic. You should start reading Vladimir Arnold's books, I bet you'll like them.
I was interested in similar stuff around a decade back, and here are my favorites that I came up with on my own (the first one is kind of funny, but the second one is genuinely nice in my opinion):
Finding the two-variable AM-GM inequality using thermodynamics
Consider the following problem:
There is an insulated chamber which is partitioned into two chambers, initially at identical conditions, by a massless movable piston. There is an ideal gas inside the chamber. The piston moves uniformly at the same speed, and the gas undergoes a quasi-static adiabatic process. Find the temperature of the chamber when the volumes are in the ratio α : β in terms of the original temperature $$$T_0$$$ and the specific heat ratio of the gas γ.
Now the answer to this problem (integrate the thermodynamic equation after using the ideal gas equation) is $$$T/T_0 = \left(\frac{(\alpha + \beta)^2}{4\alpha\beta}\right)^{\frac{\gamma - 1}{2}}$$$.
Note that the work done is negative (consider the sign of the pressure difference at every point), so the internal energy (and hence the temperature) of the gas must increase. This means $$$\frac{T}{T_0} \ge 1$$$. Also, since $$$c_P = c_V + R$$$, we have $$$\gamma > 1$$$. So by taking the $$$(\gamma - 1)$$$-th root of the inequality, we recover the AM-GM inequality for 2 variables.
Solving the tautochrone problem using Kepler's laws
This was inspired from the solution to an international Olympiad problem that I solved in-contest.
Consider the following problem:
Let two spherical bodies released of mass $$$m_i$$$, i = 1, 2 be released in isolated space, and move under gravity. Find the separation between them as a function of time. (Assume that no collisions happen, i.e. the impact parameter is very small compared to the initial separation $$$r_0$$$ but large compared to the radii of the two spheres.)
If $$$r$$$ is the separation between the masses, then by using conservation of energy in the frame of reference of the center of mass, we have $$$\dot{r}^2 \cdot \frac{1}{2G(m_1 + m_2)} = \frac{1}{r} - \frac{1}{r_0}$$$.
Also consider the following problem:
The tautochrone problem asks for the curve such that the frequency of oscillations of a point mass moving on it frictionlessly under a uniform gravitational field is independent of the amplitude, i.e., if a particle is kept on it at any point, it returns to that position after a time which doesn’t depend on the position where it was kept.
Here's how we get to an equation for it:
For a harmonic oscillator, we know that the time period is independent of the amplitude of motion. So if we have a harmonic potential with respect to arc length, we will have a motion that gives us a tautochronic potential. It is easy to see that the dependence of the potential with respect to the arclength will be unique, which can be seen from the process of building up the tautochrone starting the origin for a given time period.
Thus we have $$$U = ks^2 / 2$$$ for some constant $$$k$$$ where $$$s$$$ is the arclength from the equilibrium. Also we know that to an additive constant, the potential energy of the particle is $$$mgy$$$ where $$$y$$$ is the y-coordinate of a coordinate system lying in the plane of motion and $$$y$$$-axis along the opposite direction of the gravitational acceleration vector. So defining $$$\omega_0^2 = \frac{k}{m}$$$, we get $$$y = \frac{\omega_0^2 s^2}{2g}$$$. Taking the differential and squaring, and expressing $$$s^2$$$ in terms of $$$y$$$ and using the fact that $$$\mathrm{d}s = \sqrt{\mathrm{d}x^2 + \mathrm{d}y^2}$$$, we get $$$\left(\frac{\mathrm{d}x}{\mathrm{d}y}\right)^2 \cdot \frac{2\omega_0^2}{g} = \frac{1}{y} - \frac{2\omega_0^2}{g}$$$.
These equations seem similar (except for the $$$x, y$$$ being swapped on one side of the equation), so we will just solve the first problem using Kepler's laws and use that solution to get a solution to this problem too (with possibly different boundary conditions, but the general form is the same). To that end, we use some geometry.
Kepler's law of areal velocity (or just angular momentum conservation for central fields) concerns itself with area swept out per unit time by the path of the mass (let's say $$$m_1$$$, which is a conic. The conic here is a degenerate ellipse, with the foci at the initial location of the mass $$$m_1$$$ and the center of mass of the system. By performing a "stretch" perpendicular to the line connecting the masses (assuming that the ellipse actually had some negligible but non-zero thickness), since ratios of areas are still preserved under stretch (due to stretching being an affine transform, or just considering what happens to an infinitesimal Cartesian area element under a stretch), we can transform this ellipse into a circle. Let's consider what happens when we consider a point on the resulting circle, let's say with an elevation angle of $$$\theta$$$ from the horizontal. Then $$$r$$$ becomes $$$r_0 \frac{1 + \cos \theta}{2}$$$ and the time taken is proportional to $$$\theta + \sin \theta$$$ (the exact time is easy to find using a different Kepler's law).
It would have been pretty cool if just using the correspondence $$$r = x$$$ and $$$t = y$$$ finished the solution. However, we need a bit more work to finish it.
Define $$$f$$$ such that $$$f(\theta) = \dot{r} / a$$$ where $$$a$$$ is such that $$$f(\pi/2) = -1$$$. Then we have $$$f(\theta) f(\theta - \pi) = -1$$$. The good part about this is, we can now replace $$$f(\theta)$$$ by $$$-1/f(\theta - \pi)$$$ in the equation, to get identical forms of the equation. After translating $$$x$$$ appropriately, we get the solution $$$x = \frac{g}{4\omega_0^2}(\theta - \sin \theta)$$$ and $$$y = \frac{g}{4\omega_0^2}(1 - \cos \theta)$$$, and we're done.
Also, it's not physics per se, but I also came up with a proof of Pythagoras' theorem using only functional equations (posting here since your proof of Pythagoras theorem does not use physics strictly but just assumes some functional form — in this solution, we don't need any such assumptions):
We consider the following functional equation:
Find all functions $$$f: [\mathbb{R}^+ \cup \{0\}]^2 \longrightarrow \mathbb{R}^+ \cup \{0\}$$$ in $$$2$$$ variables satisfying the following properties:
The following solution of the functional equation is attributed to the AoPS user pco:
Setting $$$x=0$$$ in (1), we get $$$f(\sqrt{ab},\frac{a-b}2)=\frac{a+b}2$$$ (using (2) and (3)) $$$\forall a>b\ge 0$$$ Note that this equality is still true when $$$a=b$$$
Let $$$x,y\ge 0$$$. Setting in the above $$$a=\sqrt{x^2+y^2}+y$$$ and $$$b=\sqrt{x^2+y^2}-y$$$, we get $$$\boxed{f(x,y)=\sqrt{x^2+y^2}}$$$ which indeed is a solution.
Now note the following figure: let $$$\omega$$$ be a circle with center $$$A$$$. $$$B, D, E$$$ are points on the circle, and the tangent at $$$B$$$ to $$$\omega$$$ meets $$$DE$$$ at $$$C$$$. Let the midpoint of $$$DE$$$ be $$$F$$$ (Note that we can do this for any right-angled triangle $$$ABC$$$, right-angled at $$$B$$$).
Using this figure and computing $$$AC$$$ in two ways, we conclude easily that the function $$$g(x,y)$$$ which is the hypotenuse of a right triangle with legs $$$x, y$$$ satisfies our functional equation, using power of a point. Thus the function $$$g(x,y)$$$ is actually $$$\sqrt{x^2+y^2}$$$, and our proof is complete.
PS: Another way is to just consider the case where the line $$$DE$$$ coincides with the line $$$AC$$$, but this method seems somewhat distinct.
regardless the blog, how to be good like you in math? it's a newbie-sh behavior & i will get downvotes but np hope you answer.
https://old.mccme.ru//dubna//2023/courses/gaifullin.html