Fast convolution for 64-bit integers
Warning: Math ahead. You can find my reference C++ implementation at https://github.com/quasisphere/conv64
Introduction
Let (a0, ..., an - 1) and (b0, ..., bn - 1), n ≥ 1, be two tuples of elements of some ring R. By their convolution we mean the tuple (c0, ..., c2n - 2) whose elements are given by
(Here we understand that ai = bi = 0 for i < 0 or i ≥ n.)
A succinct way of encoding this is via polynomials: If A(x) = a0 + a1x + ... + an - 1xn - 1 and B(x) = b0 + b1x + ... + bn - 1xn - 1, then
Convolution can thus be understood via multiplication of polynomials and vice versa. From this point on we will exclusively work with polynomials instead of tuples since that is much more natural.
Multiplying polynomials with real or complex coefficients can be done efficiently via the Fast Fourier Transform. The same method can also be applied to polynomials with integer coefficients, but then one has to worry about possible loss of precision and therefore getting a wrong answer. In this blog we will present a way of multiplying polynomials whose coefficients are 64-bit integers, or in mathematical terms, integers modulo 264. The underlying ideas of our method are not new, but I have not seen this exact combination used before. A nice survey of fast multiplication methods is given in https://cr.yp.to/papers/m3.pdf
We note that FFT computes cyclic convolutions, that is products in the ring R[x] / (xn - 1). This is not a problem since to compute an acyclic convolution one can simply pick n large enough and zero-pad the polynomial (so that no cyclic overflow occurs).
A short recap on the Fast Fourier Transform
Assume that R is a commutative ring that contains an element ξ such that ξ2m = 1 and 2m is the multiplicative order of ξ. Then the polynomial x2m - 1 = x2m - ξ2m splits recursively into factors as follows:
Now, assume that we want to compute the product of two polynomials in the quotient ring R[x] / (x2m - 1). Then by the Chinese remainder theorem it is enough to compute their product in R[x] / (x2m - 1 - ξ2m - 1) and R[x] / (x2m - 1 - (ξ2)2m - 1). The multiplication by FFT works by doing this reduction repeatedly until we are left only with first degree polynomials of the form x - ξj for j = 0, ..., 2m - 1.
In practice FFT algorithms give you the evaluations A(ξj), which corresponds exactly to reducing modulo x - ξj. By the preceding discussion to multiply the polynomials A and B we must form the products A(ξj)·B(ξj) and then do the Chinese remainder theorem all the way up to the original ring. This second stage is done by the inverse FFT.
Outline of the method
Let R = Z / 264Z denote the ring of integers modulo 264. There are two main obstacles to multiplying polynomials in R[x] using the FFT method.
Obstacle 1: 2 is not invertible. This means that we cannot perform the standard (radix-2) FFT, since in the inverse transform we must divide by 2. The solution we will use is to instead perform a radix-3 FFT on an array whose length is a power of 3.
Obstacle 2: There are no roots of unity of order 3m. Our solution is to first adjoin a 3rd root of unity to the ring R and then manufacture higher order roots via a Schönhage-type trick.
Having identified what we must overcome, we will now outline the method. First of all, we extend our ring of scalars by looking instead at the ring T = R[ω] / (ω2 + ω + 1). Its elements can be represented as a + bω, where a and b are 64-bit integers and the ring of 64-bit integers is embedded in it as the elements with b = 0. The product of two such elements is given by
where we have used the fact that ω2 = - ω - 1, and it is also easy to check that we have ω3 = 1. Thus ω is a 3rd root of unity in this ring. We say that the conjugate of an element a + bω is the element we get by mapping ω → ω2, that is a + bω2 = a - b - bω.
In what follows we will devise an algorithm for multiplication in T[x] / (xn - 1) where n is a power of 3. Assume that we are given a polynomial a0 + a1x + ... + an - 1xn - 1 with ai from the extended ring T. We will first let y = xm, where m and r are powers of 3 such that mr = n and 3m ≥ r. Then we can write our polynomial in the form
Notice that in a program this does not require us to do anything since the order of the coefficients stays the same.
Now since the coefficients of yis are polynomials of degree at most m - 1 and yr = xn = 1, we can think of this as an element of the ring T[x] / (x2m + xm + 1)[y] / (yr - 1). Clearly if we multiply two such polynomials the products of the coefficients in T[x] / (x2m + xm + 1) will not overflow, and we can deduce the result of the original multiplication.
But we can reduce the problem even further! We have x2m + xm + 1 = (xm - ω)(xm - ω2). Thus, if we can deduce the products in the rings T[x] / (xm - ω)[y] / (yr - 1) and T[x] / (xm - ω2)[y] / (yr - 1), we will be done by the Chinese remainder theorem. Now in either case x itself is a 3mth root of unity, so we can use FFT to compute the products, assuming that we have an efficient method of calculating products in T[x] / (xm - ω) and T[x] / (xm - ω2).
But this we can solve recursively! Indeed, the method of computing products in T[x] / (xn - 1) we have outlined goes through almost identically also in the case of T[x] / (xn - ω) and T[x] / (xn - ω2). The only difference is that we will end up with a ring T[x] / (xm - ω)[y] / (yr - ω) (in the first case, the second case is similar), which we can map to the ring T[x] / (xm - ω)[y] / (yr - 1) by mapping y → xm / ry. This requires that m ≥ r, which is a bit (but not significantly) worse than the condition 3m ≥ r we had earlier.
Details and optimizations
When implementing the above strategy, it is useful to notice a couple of things.
On the first round of the recursion when we are working in the ring T[x] / (xm - ω2)[y] / (yr - 1), we note that we can map this to the ring T[x] / (xm - ω)[y] / (yr - 1) by conjugation. Since our original data came from ordinary 64-bit integers, conjugation performs as identity on them. Hence the product in T[x] / (xm - ω2)[y] / (yr - 1) is just the conjugate of the product in T[x] / (xm - ω)[y] / (yr - 1) and it is enough to only compute the latter.
On further rounds of the recursion we can assume that we are always trying to multiply in T[x] / (xm - ω). Indeed, when we would need a result in T[x] / (xm - ω2)[y] / (yr - ω), we can map this by conjugation to T[x] / (xm - ω)[y] / (yr - ω2) and then perform the change of variables y → x2m / ry to get to T[x] / (xm - ω)[y] / (yr - 1) and proceed using FFT as usual.
The element of T[x] / (x2m + xm + 1) that is f modulo xm - ω and g modulo xm - ω2 is given quite concretely by 3 - 1(1 + 2ω)(g(xm - ω) - f(xm - ω2))
The radix-3 FFT is a rather standard modification of the regular radix-2 FFT, so we will not go through it here. The twiddle factors will be powers of x, and therefore one just needs a simple function that lets one compute the product xtp for p in T[x] / (xm - ω). This same function can also be used for the linear changes of variables in the earlier steps.
Conclusion
We have outlined an algorithm for computing exact convolutions modulo 264. All the computations are conveniently done modulo hardware. Other methods for exact convolutions include rounding of floating point convolutions, convolutions modulo suitable primes and the Nussbaumer/Schönhage-tricks. The algorithm here is close in spirit to the latter two, but the implementation is simplified because of the extension of scalars. In particular no zeropadding of the polynomials is needed.
Regarding speed: I haven't tested too much, but it seems reasonably fast, even compared to regular FFT algorithms (not optimized competitive programming snippets).
I'm happy to hear comments or about other interesting approaches! As it is, the code is on the border line of being competition ready. It certainly works if you can copy-paste but writing it down by hand requires some time. In my implementation there are a lot of long comments, so it's not quite as bloated as it might seem at first, however.









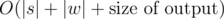 .
.

