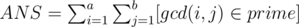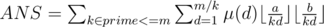Hi,
Recently I learned some of the basics of the hill climbing search. I have successfully used some of the versions to solve a few problems. For discrete domain, it worked as expected most of the time like solving n queens for board of 300 size.

Now, for continuous domain it doesn't works as expected. Although I have solved a few (e.g. Bike Roads from ASC 23 by climbing over two variable theta = [-PI PI]), it was more like a trail and error than a careful design.

As of my current understanding, to optimize(minimize) a function over multivariate continuous domain, I need to make it discrete. The smaller the cell division, the better(less error). For the problem(doesn't require to read it to understand my argument), 106E - Космические спасатели the function we optimize can return a error of 4*10^12*error_in_data. So, making the cell 10^-20 unit apart should be good enough as the error 10^-6 is allowed, otherwise all the ternary search would have failed too IMO.

But, it would make the grid so big. So, instead we use a bigger cell division say 500 apart, then find the minimal point by moving to the adjacent lower point until we can reach a minima. but, which of course have a great error, but the solution is near. Hence, we now divide the grid into twice smaller cell and improve from it. The process continue until we reach the targeted 10^-20 cell division.

I don't see a flaw in this approach. The function is convex, can be optimized with GSS. No place where we accumulate error. But still I ended up in a point which has a error 10^-2. I submitted the problem so many times that I don't know which one to link. So, instead give me some insight about when the method is to be chosen over GSS. And how to control/estimate the error. If there is a flaw in my understanding point it out.

Here is a implementation found online.
An adapted version which is a modification of the previous one to eliminate the fixed number of iteration (As I thought that might be a issue here).

Any resource suggestion will be good enough. :)

Please suggest some problems solvable using general matching/packing.

Problem: https://www.codechef.com/problems/D4
Submission: https://ideone.com/fuoYkk

The problem asked how many gcd(i, j) are prime, where 1 <= i <= a, 1 <= j <= b.

This is the first time I am studying mobius inversion. I modeled the problem as of many example given in: https://codeforces.com/blog/entry/53925

Which easily leads to,

This requires 3 * 10⁷ iteration for worst case. Due to tight time limit, this is huge. But I can't reduce it any further. Any hint will be helpful.

Many people on different articles suggests that if an optimization problem has a greedy solution, the underlying structure must have matroid property.

I was trying to understand this. So far, I was able to prove that for,
1. Maximum sum of m integers among n integer.
2. Minimum spanning tree.

However, The classical greedy algorithm Activity Selection seems to fail having exchange property.

Let,
E = {1-3, 2-4, 3-5, 4-6, 5-7}

Now, Take two independent set,
I = {2-4, 4-6} and J = {1-3, 3-5, 5-7}

There is no activity in J which can extend I. Which fails the exchange property of matroid, if I understood it correctly. Thus, it is not matroid and shouldn't have a greedy algorithms.

Where am I wrong?

NB:
1. a-b means starts at time a end just before time b.
2. I know matroid is not best way to find greedy algorithms in contest. I just like to understand the underlying structure once.

EDIT:
Please Suggest some math forum where I may get the answer.

UPDATE
Well, I got the answer. In strict sense, the activity selection algorithm is called greedy-like not greedy. That is the reason. There are many algorithm which we take as greedy but they aren't greedy in mathematical sense. They are just greedy-like. This also explain how many people misguiding others that you should prove the matroid property when solve greedy problem. Fortunately, many people also suggest not to use matoroid as an criteria.

Problem: 375E - Red and Black Tree

At first, the editorial seems like using black and red in the opposite meaning than the problem. If someone can edit the editorial than it would be good for newcomer because this problem is really an interesting one and many people will learn the concept of integer programming from this at first. (I googled to get some problem on LP and found this. Then read the editorial and a book on IP formulation, and It was really confusing until I really believed, the editorial is not always perfect.)

My solution: 35949315

The time limit is 1s and it passed in 935ms. Is it OK for an LP like this? I didn't wrote the template. And I do not also know its time complexity. There is a entire book on this. Which is not good (for now). Can you give an intuitive idea about the complexity?

I am concerned with 2 cases
1. This maybe with the simplex implementation. Maybe someone can help to verify this if it is good.
2. I used n+2 constraints. I don't know what is the standard technique to replace equality with inequalities without dividing it into 2. Is it the correct approach?

And finally,
Suggest me some problem on linear programming. I have solved 375E, 605C on CF and another one on HackerRank.

Thanks for your time. :)

Problem: http://www.spoj.com/problems/IQUERY/

I think we can use segment tree for this problem. I figured out that the multiplication and addition part has the following property:
mul(i, j) = mul(i, k)+mul(k+1, j)+mul(i, k)*mul(k+1, j) where i <= k <= j.
So, this is easy to do with range trees.

But as bitwise and is not distributive over addition we can't define the second type of query as the previous one. Anyone approached the problem?

Any hint will be appreciated.

I planned to write an tempermonkey script for codeforces, that will help me copying multi-test inputs. But As i didn't write javascript for years, I wanted to make use of the chrome console.

Here is a screenshot!

The script codeforces.js is pinging to some server and flooding the debug console. Is it intended or done by mistake? It makes my job harder :(

Nothing is well understood unless we can apply it to solve some problems. Currently, I am learning number theory and there is no good classified list of problems for number theory. So, It is difficult to find some problem based on a specific topic.

Here I will maintain a list of problems of number theory in a few category. So, In near future, nobody have to face the same problem. Contribute interesting problems, people(mostly me :D ) will be grateful to you.

1. Divisibility/Primes/Co-prime/GCD/LCM
Problems:
1. LOJ: 1014, 1035
2. CF: 230B, 711E, 585E, 585C, 222C, 546D, GYM101212B
3. SPOJ: LCMSUMH
4. E-OLYMP: 1146, 1243, 1147, 1229, 1244, 1230

2. Continued Fraction
Problems:
1. UVA: 834
2. HackerRank: euler064

3. Diophantine Equations
Problems:
1. LOJ: 1077
2. CF: 7C

4. Functions: Counting Divisors/Divisor Sum
Problems:
1. LOJ: 1054
2. UVA: 13083

5. Function: Totient and Similar
Problems:
1. LOJ: 1007
2. SPOJ: NFACTOR , NDIV

6. Modular Arithmetic/CRT
Problems:
1. LOJ: 1067
2. CF: 687B, GYM100825A

7. Discrete Logarithms
Problems:
1. LOJ: 1325

8. Number Systems
Problems:
1. LOJ: 1028
2. E-OLYMP: 1001, 1002, 1008, 1013

9. Primitive Root
Problems:
1. E-OLYMP: 647

NB: This list is just created. And hopefully will grow with user contribution and as I learn. Thanks for being a part of it. :)

Contributors:
HaabyHings, Rudy1444, Lucas97, Batman, t3rminated, MladenP, TooNewbie

I am trying to understand continued fraction. But I am unable to understand a statement from SY Yan's book.

Say, a/b = [q0, q1, ...., qn] where qi's are the partial quotients of the fraction. Then, the kth convergent of this fraction is the fraction which have a representation denoted by [q0, q1, ...., qk].

Now, lets the kth convergent is Ck. Then, Ck = Pk/Qk = (qk*Pk-1 + Pk-2)/(qk*Qk-1 + Qk-2) .... (1)

So far I have verified the statements and they are consistent.

But, then Yan stated that, if, Pk = qk*Qk-1 + Qk-2 and Qk = qk*Pk-1 + Pk-2, then GCD(Pk, Qk) = 1 ...... (2)

But, How it can be? As, (2) and (1) impiles Pk/Qk = Qk/Pk, implies Pk = Qk. What did I miss?

Problem link: http://www.lightoj.com/volume_showproblem.php?problem=1018

Verdict: TLE — O(n^2 * 2^n) solution

Code: http://ideone.com/7JjcIX

I transformed the problem into this. The idea is to given N integer 0 <= N < 2^M where M <= 16, find the minimum number of integer needed to make 2^M-1 by the operation bitwise-OR. My solution is a variation of subset sum as it is the only DP algorithm I know. But, The test cases are huge, 1000. Can you suggest a better approach? Thanks for your attention.