If you've ever taken some lessons on competitive programming, chances are that you have already heard about one of the most famous formula: the Möbius inversion. This article is aimed to provide some basic insight on what is the Möbius inversion, as well as how to apply it in various programming tasks.
Prequisite
If you are not familiar with the linear sieve and multiplicative functions, it is recommended that you read about them first here.
I will introduce some frequently used notations and lemmas first.
Notation
- [P] refers to the boolean expression, i.e. [P] = 1 when P is true, and 0 otherwise.
- ⌊ x⌋ refers to rounding x down to the nearest integer. Thus
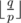 refers to the integer division.
refers to the integer division. - d|n means that d can divide n (without a remainder).
The following functions are all multiplicative functions, where p is a prime number and k is a positive integer.
- The constant function I(pk) = 1.
- The identity function Id(pk) = pk.
- The power function Ida(pk) = pak, where a is constant.
- The unit function
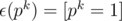 .
. - The divisor function
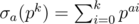 , denoting the sum of the a-th powers of all the positive divisors of the number.
, denoting the sum of the a-th powers of all the positive divisors of the number. - The Möbius function μ(pk) = [k = 0] - [k = 1].
- The Euler's totient function φ(pk) = pk - pk - 1.
Lemma
I have some my unofficial names for these frequently used conclusions. If you happen to know any more commonly used name for them, you are more than welcome to tell me.
- ( The integer division lemma ) For every positive integer p, q and r,
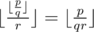 .
.
Proof: We know that 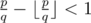 . Hence
. Hence 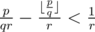 . Since the fraction part of
. Since the fraction part of 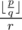 cannot exceed
cannot exceed 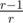 , we achieve the conclusion.
, we achieve the conclusion.
- ( The harmonic lemma ) Consider the harmonic sequence on integer division
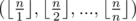 .
.
- The sequence is non-increasing, and there are at most
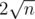 different elements.
different elements. - The sum of the sequence is approximate to
 .
.
Proof: Denote 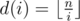 . For every i not exceeding
. For every i not exceeding  , there will be no more than
, there will be no more than  values in the domain of d(i), so there can be at most
values in the domain of d(i), so there can be at most  different values for d(i). For the rest part of i greater than
different values for d(i). For the rest part of i greater than  , we can infer that
, we can infer that 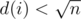 and is a positive integer, so there can be at most
and is a positive integer, so there can be at most  different values for d(i). Therefore we know that there are at most
different values for d(i). Therefore we know that there are at most 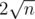 different elements in the sequence.
different elements in the sequence.
Since the Euler–Mascheroni constant states that 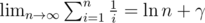 , we know that
, we know that 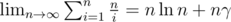 , so the sum of the original sequence is approximate to
, so the sum of the original sequence is approximate to  .
.
Moreover, it is actually possible to exploit the property that the sequence has at most 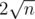 different elements, and write a loop that runs in
different elements, and write a loop that runs in  complexity to iterate through every possible value of d(i), using the fact that the greatest integer x satisfying d(x) = d(i) is
complexity to iterate through every possible value of d(i), using the fact that the greatest integer x satisfying d(x) = d(i) is 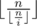 . The piece of code below demonstrates one way to program it.
. The piece of code below demonstrates one way to program it.
for (int i = 1, la; i <= n; i = la + 1) {
la = n / (n / i);
//n / x yields the same value for i <= x <= la.
}
- ( The transitive property of multiplicative functions )
- If both f(x) and g(x) are multiplicative, then h(x) = f(x)g(x) is also multiplicative.
- If both f(x) and g(x) are multiplicative, then their Dirichlet convolution
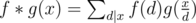 is also multiplicative. Specifically, if f(x) is multiplicative,
is also multiplicative. Specifically, if f(x) is multiplicative, 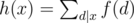 is also multiplicative.
is also multiplicative.
The proof is more mathematical, which I will skip here.
What is the Möbius inversion?
According to Wikipedia, the Möbius inversion states that:
If 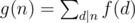 for every positive integer n, then
for every positive integer n, then 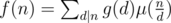 , where μ(x) is the Möbius function, which is multiplicative and satisfies f(1) = 1, f(p) = - 1, f(pk) = 0 for any prime number p and any integer k ≥ 2. ( It is worth noting that you can pre-compute all values of the Möbius function from 1 to n using the linear sieve. )
, where μ(x) is the Möbius function, which is multiplicative and satisfies f(1) = 1, f(p) = - 1, f(pk) = 0 for any prime number p and any integer k ≥ 2. ( It is worth noting that you can pre-compute all values of the Möbius function from 1 to n using the linear sieve. )
However, the definition alone does not mean much (unless the problem statement explicitly gives you something like 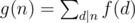 . In that case, well...). There is one important property that is probably more useful than the definition:
. In that case, well...). There is one important property that is probably more useful than the definition:
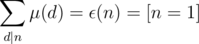
In order to prove this property, we have to use the transitive property of multiplicative functions to show that 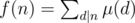 is multiplicative. After that, we can see f(1) = 1 and f(pk) = 0, which means f(x) = ε(x). Now you may ask: why is this property important? I think it is best to show the reasons in some basic examples below.
is multiplicative. After that, we can see f(1) = 1 and f(pk) = 0, which means f(x) = ε(x). Now you may ask: why is this property important? I think it is best to show the reasons in some basic examples below.
Example 1. Find out the number of co-prime pairs of integers (x, y) in range [1, n].
Solution 1. Notice that the question is the same as asking you the value of
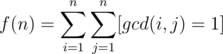
Now apply the Möbius inversion on [gcd(i, j)] = 1, we have
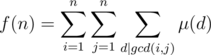
which is the same as
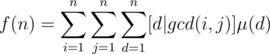
Notice that [d|gcd(i, j)] = [d|i][d|j]. Therefore
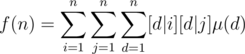
We can change the order of summing things up, so
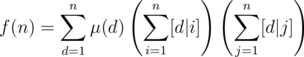
We know that 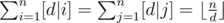 . Thus
. Thus
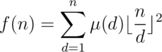
Then we can simply loop through 1 to n to compute the formula. While we can optimize this loop to  using the harmonic lemma, we still have to use the linear sieve to pre-compute the values of μ(d). Therefore, the overall complexity of the algorithm is O(n).
using the harmonic lemma, we still have to use the linear sieve to pre-compute the values of μ(d). Therefore, the overall complexity of the algorithm is O(n).
Example 2. Find out the sum of gcd(x, y) for every pair of integers (x, y) in range [1, n] (gcd(x, y) means the greatest common divisor of x and y).
Solution 2. Similar as above, notice that the question is the same as asking you the value of
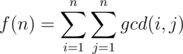
Let k = gcd(i, j). We can then loop for k first.
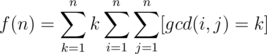
Now assume i = ak, j = bk, and then
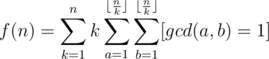
It can be observed that the last part of the formula is the same as the one in example 1. Applying the same procedure, we have
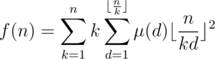
According to the harmonic lemma, 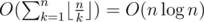 . Therefore, if we compute the sum above with brute force, the overall complexity will be
. Therefore, if we compute the sum above with brute force, the overall complexity will be  .
.
This is, however, not the best complexity we can achieve with the Möbius inversion. Now let l = kd, and we can loop for l first.
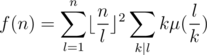
Applying the transitive property of multiplicative functions, we can see that 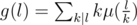 is multiplicative. Moreover, we have g(pk) = pk - pk - 1. If you have somewhat studied about the number theory, you may figure out that g(l) is actually the Euler's totient function. Regardless of whether you know about the coincidence or not, g(l) can be pre-computed with the linear sieve, and
is multiplicative. Moreover, we have g(pk) = pk - pk - 1. If you have somewhat studied about the number theory, you may figure out that g(l) is actually the Euler's totient function. Regardless of whether you know about the coincidence or not, g(l) can be pre-computed with the linear sieve, and 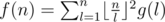 , which can be simply computed in O(n) complexity.
, which can be simply computed in O(n) complexity.
Example 3. Find out the sum of lcm(x, y) for every pair of integers (x, y) in range [1, n] (lcm(x, y) means the least common multiple of x and y).
Solution 3. Well, we should be pretty familiar with the techniques by now. First of all, the answer should be
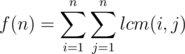
Since 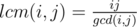 , let k = gcd(i, j). We can then loop for k first.
, let k = gcd(i, j). We can then loop for k first.
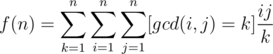
Now assume i = ak, j = bk, and then
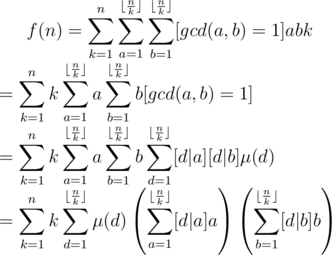
Now let's proceed to assume a = dp, b = dq, then
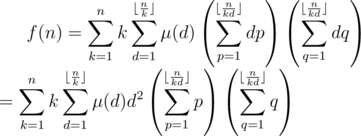
Now notice 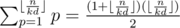 , and we have
, and we have
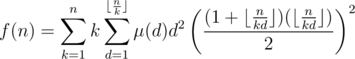
Now following the example above, let l = kd, and then
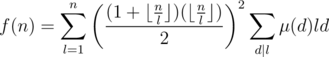
Notice that 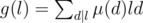 is also multiplicative, and g(pk) = pk - pk + 1. We can pre-compute the values of g(l) via the linear sieve, and
is also multiplicative, and g(pk) = pk - pk + 1. We can pre-compute the values of g(l) via the linear sieve, and 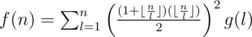 . The overall complexity will be O(n).
. The overall complexity will be O(n).
Example 4. Find out the sum of lcm(A[i], A[j]) for every pair of integers (A[i], A[j]) with an array A of length N (1 ≤ i, j ≤ N), with the constraint of 1 ≤ N ≤ 200, 000 and 1 ≤ A[i] ≤ 1, 000, 000.
Solution 4. This is a common variation of the example above. Denote
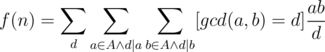
We simply have
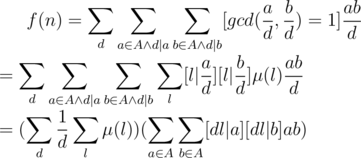
Let t = dl, then
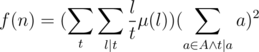
Now, similar to the example above 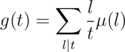 is multiplicative with g(pk) = p - k - p - k + 1, and thus can be computed with O(V), where V is the range span of A. The latter part of the formula
is multiplicative with g(pk) = p - k - p - k + 1, and thus can be computed with O(V), where V is the range span of A. The latter part of the formula  is also fairly easy to figure out if you keep track of the number of the elements equal to v as cnt(v), since
is also fairly easy to figure out if you keep track of the number of the elements equal to v as cnt(v), since
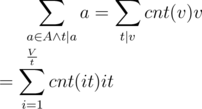
and with the harmonic lemma, the above computation can be done in 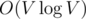 . Hence the overall complexity is
. Hence the overall complexity is 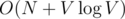 .
.
Practice Problems
Simple Sum
(Thanks Bashca for showing me this one!)
GCD
Sky Code
Extensions
It is known that all examples above can be further optimized to 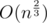 . The exact technique will (probably) be introduced in the upcoming article.
. The exact technique will (probably) be introduced in the upcoming article.
Update: The article introducing the optimization is ready here.
Finally, thanks Tommyr7 for his effort in the article!











Excellent tutorial. If you don't mind can you just write down in 1-2 sentences how to precompute the Mobius function using linear sieve ?
See the example for the Euler's totient function in the linear sieve tutorial.
For the Möbius function the three cases are:
1) if x is prime: mobius[x]=-1 (obiously the number of prime factors of a prime number is odd)
2) x=ip and i%p!=0: mobius[x]=mobius[i]*mobius[j] (since the function is multiplicative)
3) x=ip and i%p==0: mobius[x]=0 (p^2 divides x)
Can you explain how to use Mobius inversion in The GCD problem link given here. I am having problem in using the theory given the that problem.
Step 1: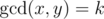 if and only if
if and only if 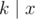 ,
, 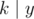 and
and  . Using this we can reduce the problem of finding 0 < x ≤ b, 0 < y ≤ d such that
. Using this we can reduce the problem of finding 0 < x ≤ b, 0 < y ≤ d such that 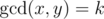 to the problem of example 1.
to the problem of example 1.
Step 2: The sum over the interval [a, b] × [c, d] is the sum over [1, b] × [1, d] minus [1, a - 1] × [1, d] minus [1, b] × [1, c - 1] plus [1, a - 1] × [1, c - 1].
Please notice that, (x=5, y=7) and (x=7, y=5) are considered to be the same.How you dealt with the condition that there should be unique pairs?
Firstly, note that a and c are both equal to 1 in the problem statement. Now, let's first handle the corner cases:
Let m = min(b, d). If k = 0 or m < k, the answer is clearly 0.
Now, firstly we obtain the answer without worrying about duplicate entries. It'll be computed by the formula given by newCEA.
After this, now let's eliminate all the duplicate values. Firstly, note that the duplicate pairs must have both the values lying within the range [1, m] because the remaining nos. from the 2 given ranges that are not lying within this range must be present in exactly one of the ranges and therefore cannot contribute to duplicates. Let X be the answer to the original problem that includes the duplicates entries, i.e., the no. of co-prime pairs between the ranges [1, b] and [1, d]. Now compute Y = no. of co-prime pairs where both numbers lie between the range [1, m]. Note that there must be exactly one pair (x, y) where x = y, and that is (k, k). For all other pairs x ≠ y, so (x, y) and (y, x) must both appear in the answer as a co-prime pairs, so there are only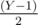 duplicate values and these are also the only duplicate values present within the ranges [1, b] and [1, d]. So, the final answer is
duplicate values and these are also the only duplicate values present within the ranges [1, b] and [1, d]. So, the final answer is 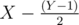 . Here is my solution for this problem as a reference.
. Here is my solution for this problem as a reference.
In your formula, the last must term must be
The max must be replaced with min.
how is the greatest integer x satisfying d(x) = d(i) is n/(n/i)?
We know that for two positive integers a, n: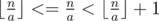
Let's define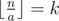
a * k <= n < a * k + a
a * k <= n and a * (k + 1) > n
So, if for a positive integer x,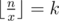

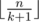 < x <=
< x <= 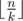
But

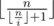 < x <=
< x <= 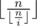
This tells us that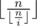 is the maximum x for which
is the maximum x for which 
If for some $$$x$$$ you have $$$\lfloor \frac{n}{x} \rfloor = k$$$ then the greatest $$$x'$$$ such that $$$\lfloor \frac{n}{x'} \rfloor = k$$$ is $$$x' = \lfloor \frac{n}{k} \rfloor$$$ because $$$\frac{n}{\frac{n}{k}} = k$$$ and if you divide $$$n$$$ by any bigger number than $$$\frac{n}{k}$$$ you get a smaller quotient than $$$k$$$.
What is the intended complexity in Sky Code? My N d(N) q solution gets TLE immediately. (N = 10000)
Precomputing the divisors of all numbers from 1 to 10000 gets AC on the problem. Using square root factorization gets TLE.
Moreover, we have g(p^k) = p^k - p^(k - 1).How did you conclude this?Update: I solved it for prime p and then generalized it for some p^k. Is it the right way?
So in example 1, step 2, did he just say that f = f ◦ μ?
How does one conclude from
that
Ah, I see, he just rewrote what was the dirichlet identity.
Duh doy, heh.
Very good tutorial. Thanks a lot!
Here is an easier version of the Sky Code problem. It asks to find co-prime triples, whereas in Sky Code, we are required to find co-prime quadruples (4-tuples).
now i know how bad my math is
Bob and Numbers How to solve this problem using the technique used in the above examples?
Can you explain the mobius inversion in the simple sum?
We have that:
Rearranging the sums:
Let l = i/k and divide by k in the second sum:
Using mobius inversion:
Rearranging the last 2 sums:
Due to symmetry, we can replace k by n/k, getting:
Which as shown in the article is:
Using properties mentioned in the article, we notice that k and φ(k) are multiplicative and therefore so is their product. Now since kφ(k) is multiplicative, so will its dirichlet convolution with the constant function be. In essence, f(n) is multiplicative and therefore we can precompute f(n) with a linear sieve.
Using the fact that φ(p^k) = p^k - p^(k-1), we can see that:
This editorial might also help, although it does not use the mobius function. That's it, hope I helped!
Thanks
can you explain LCM Sum using mobius function please? It would help a lot. Thank you.
Do you mean Example 3? If you do, since it's already explained, could you point out what you don't understand?
Thank you for paying attention , i got the example 3 , the only problem i am getting is i am not able to find the formula(using mobius inversion) for problems in which
i is varying from 1 to n
j is varying from i+1 to n
like GCDEX2
if both are varying from 1 to n then there is no problem.
can you help me in this please?
thank you .
yes, I am threat, this is exactly my solution, thanks.
can anyone please explain how mobius inversion is used to convert [gcd(i, j)] = 1 to summation d|gcd(i , j) u(d) ? please help me , i am stuck on this from last 2-3 days
Simply substitute $$$n=gcd(i,j)$$$ in this formula.
thank you so much , it really helped
How to interpret mobius inversion two forms equivalent to functions f(n) and g(n). For example in Vandermonde convolution we have a combinatorial interpretation which makes the resulting formula intuitive. Basically, I want to know why does the divisors comes into formulaes? Or does there exist a counting problem where counting them in two different ways results in the inversion by mobius? Nisiyama_Suzune
This may be helpful to get the intuition. (https://youtu.be/_noJI8UkTq8)
Oh, the famous necklace problem. No one ever mentions usage of mobius function while describing Burnside lemma.
In example 3, the sum of LCM(i,j), once we get to
can't we deduce an O(n log n) algorithm straightaway, since the above is
(is this step correct?) and for fixed $$$n$$$, $$$k$$$ it should be straightforward to work out
in O(1)?
Yes, you are right.
Still, for the sake of argument, one would need to show how to compute that in $$$O(1)$$$, which is basically what I was doing below. :)
Another practice problem: E — Sum of gcd of Tuples (Hard).
This is the n-tuple version of example 2.
Help with GCD_Pair_Array_Query problem.
This might help: RANDCHCL Editorial
Here the editorialist discusses about computing the sum of gcd(Wi,Wj) for an array 'W' in a really simple manner (in O(nlogn)).
Soln — https://ideone.com/32tjY8 https://imgur.com/E6p36i6 (This is how i tried, might be wrong)
Nisiyama_Suzune is this type of problems are solvable with mobius inversion?
It seems that a lot of people are asking so I have updated the article to include it as the 4th example.
Thank you! <3
I think after assuming, t = dl; the expression should be like this: $$$ (\sum\limits_{t}\sum\limits_{l|t}\frac{l}{t}\mu(l))(\sum\limits_{a \in A ^\wedge t|a}a)^2 $$$
rather than this: $$$ (\sum\limits_{t}\sum\limits_{l}\frac{l}{t}\mu(l))(\sum\limits_{a \in A ^\wedge t|a}a)^2 $$$
Yes, you are right. Sorry for the typo. :(
In example 1,
when you calculate the number of co primes, shouldn't you multiply 1/2 to f(n) since you're counting counting twice? i.e both [gcd(x,y)=1] and [gcd(y,x)=1]
It's möbing time!
the GCD problem has a chinees judje that requires verification with a chineese number :(