This is a follow-up blog to this talk Please let me know if there are any errors. I might not be able to reply rapidly as it is finals week for me.\
The previous post doesn't exactly explain how to actually work out the solutions to Sprague-Grundy problems, or how to code them. Within this follow-up blog, I shall attempt to explain some of my thought process on working through Sprague-Grundy and similar problems, as well as including some code.
First, some pseudo-code of calculating the Sprague-Grundy, and how to find the MEX.
However, this implementation is inefficient, as it's not memoized, and we might recompute Sprague-Grundy of certain games quite a lot. Usually, if the game is just in terms of stack size, we can just go in increasing order to evaluate, since each move reduces the stack size, and we would have stored the values for smaller stacks into an array. This is a fairly simple example of dynamic programming.
Consider a game where we're given a set S of numbers by which we can reduce the size of a pile. The following outlines how to use an array to calculate the Sprague-Grundy of a single pile.
Now, since we've computed the Sprague-Grundy for any given pile, we can determine who wins given a list of piles in the starting position in linear time. The S-Nim problem on kattis is basically these.
Sometimes, a turn on a game results in a combination of games of the same type. This is usually a strong indication for the usage of Sprague-Grundy. As an example, let us consider the Cuboid Slicing Game.
Each move can result in up to 8 different games of the same type. We consider any 0-volume cuboid as a losing position, as no further moves can be made upon it.
However, calculating the set of all possible next games might seem intimidating, but we can compute the Sprague-Grundy of game combinations using the Sprague-Grundy of the original games!
Let us first consider a pseudo-code of the recursion.
Converting this recursive definition to a solution that runs fast enough is left as an exercise. Additionally, some constant-factor optimizations may be needed.
Some further problems I could find are as follows:
One of the techniques mentioned in the previous post can be used for this problem: 717D - Dexterina’s Lab
In addition, there are quite a few problems on ProjectEuler that these concepts are also applicable to.
Now, for outlines of solutions to the problems from the previous blog:
Since someone was asking for the proof of the Sprague-Grundy Theorem, since it was omitted for brevity in the previous post, here is one.



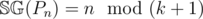 . This can be proven by strong induction.
. This can be proven by strong induction.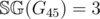 ,
, 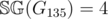 .
. 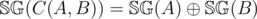
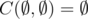 , and
, and 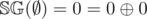 . Let
. Let 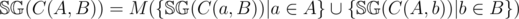 Since
Since 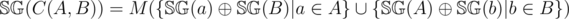 Hence,
Hence, 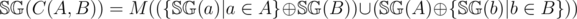
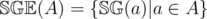 , then
, then  . Also, the above becomes.
. Also, the above becomes. 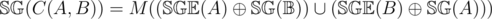
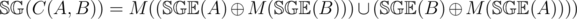
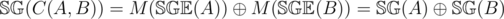






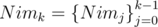
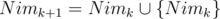
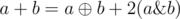 , where
, where  , except the bit is 1 if and only if both bits are 1. We can see this by noting that shifting left in binary is equivalent to multiplying by
, except the bit is 1 if and only if both bits are 1. We can see this by noting that shifting left in binary is equivalent to multiplying by  represents where carries do not need to occur.
represents where carries do not need to occur.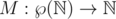 , where
, where 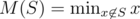 Equivalently stated,
Equivalently stated,  . Then, let
. Then, let 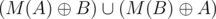 .
.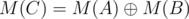 .
. cannot be in
cannot be in 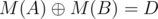 is in
is in 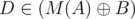 or
or 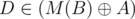 . Assume WLOG, that it is at least in
. Assume WLOG, that it is at least in 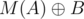 , then
, then 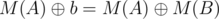 for some
for some 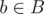 . Thus,
. Thus, 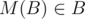 , which is a contradiction. Therefore,
, which is a contradiction. Therefore,  are in
are in 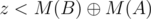 . Let
. Let 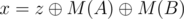 .
. 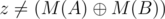 . Consider the largest bit that is set in
. Consider the largest bit that is set in 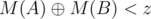 , as the most significant bit that differs is larger in
, as the most significant bit that differs is larger in 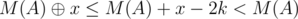 , so
, so  . Let
. Let 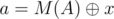 . Then,
. Then,  , as desired.
, as desired.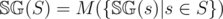
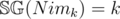 can be proven through strong induction. Since
can be proven through strong induction. Since 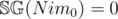 . Now, if we assume that
. Now, if we assume that  for all
for all 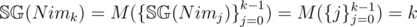 This completes the inductive step, so
This completes the inductive step, so 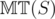 be the maximum number of moves a game
be the maximum number of moves a game 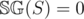 . Note that if
. Note that if 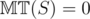 , then there are no moves, so we have a lost game and
, then there are no moves, so we have a lost game and 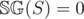 , so the base case is finished.
, so the base case is finished.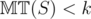 , it is true. Consider a game
, it is true. Consider a game 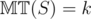 . If
. If 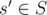 ,
, 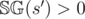 , from the definition of the Sprague-Grundy function. Thus, since
, from the definition of the Sprague-Grundy function. Thus, since 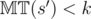 , all turns in this game lead to a winning games for the next player by the inductive hypothesis. Thus,
, all turns in this game lead to a winning games for the next player by the inductive hypothesis. Thus, 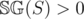 , then there is a game
, then there is a game 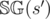 is
is 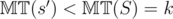 ,
, 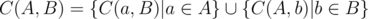 Theorem:
Theorem: 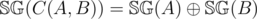 . Proof omitted for brevity, but it can be proven inductively on the value of
. Proof omitted for brevity, but it can be proven inductively on the value of 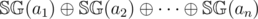
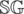
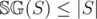 is obvious from the definition of Mex. In addition,
is obvious from the definition of Mex. In addition, 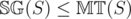 , as from any state with Sprague-Grundy value of
, as from any state with Sprague-Grundy value of 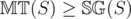 , as desired.
, as desired. 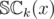 be the number of valid lists of
be the number of valid lists of 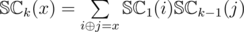 .
.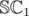 and
and 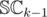 , which we will denote as
, which we will denote as 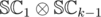 . Since XOR-convolution is associative, we want to actually compute
. Since XOR-convolution is associative, we want to actually compute 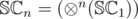 . The number of losing positions is
. The number of losing positions is 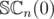 .
. 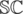 can thus be calculated in
can thus be calculated in  XOR-convolutions by binary exponentiation.
XOR-convolutions by binary exponentiation.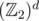 , where XOR becomes bitwise addition. Thus convolution can be performed with a normal
, where XOR becomes bitwise addition. Thus convolution can be performed with a normal 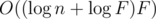 time to finish it overall. This is much smaller than
time to finish it overall. This is much smaller than 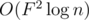 , and should be enough to solve it for most problems we would come across, if we can calculate the counts of each value of the Sprague-Grundy quickly.
, and should be enough to solve it for most problems we would come across, if we can calculate the counts of each value of the Sprague-Grundy quickly.
