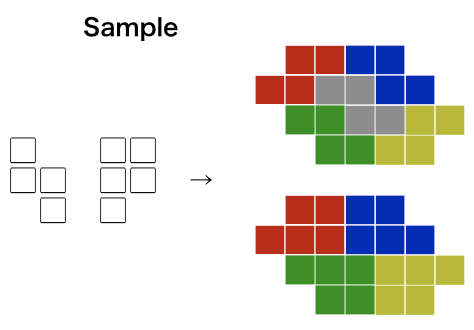
We will hold Tokio Marine & Nichido Fire Insurance Programming Contest 2023(AtCoder Beginner Contest 307).
- Contest URL: https://atcoder.jp/contests/abc307
- Start Time: http://www.timeanddate.com/worldclock/fixedtime.html?iso=20230624T2100&p1=248
- Duration: 100 minutes
- Number of Tasks: 8
- Writer: kyopro_friends, math957963, evima, m_99, Nyaan
- Tester: MMNMM, leaf1415
- Rated range: ~ 1999
- The point values will be 100-200-300-400-475-550-550-600.
We are looking forward to your participation!