Problem A. Chat room
Solution is greedy algorithm. The first thing we do is find in our string the first letter 'h'. Then we find letter 'e' which is righter that found 'h'. If we find the whole word 'hello' in such way, obliviously, answer is YES.
Now let's prove that if answer exists, we find it. Let see on position of the 'h' in right answer. If we move it to the first 'h' in our string, nothing changes. But now we can say that our greedy algorithm correctly Now let's do such with the second letter, and so on.
We have greedy algorithm with work time O(n), where n - length of the input.
Now let's prove that if answer exists, we find it. Let see on position of the 'h' in right answer. If we move it to the first 'h' in our string, nothing changes. But now we can say that our greedy algorithm correctly Now let's do such with the second letter, and so on.
We have greedy algorithm with work time O(n), where n - length of the input.
Problem B. Coins
This problem also have greedy solution: we run down all number from 2 and greater and while denomination of the last added to answer coin is divisible by current number, we divide and increase answer.
You can prove correctness, if you take a look at prime factorizations of coins' denominations. In each next denomination each prime have less or equal power than the current one (it's equivalent to 'a divide b'). Obliviously, if summary degree of primes decreases at least two (for example, we had numbera = x· y· z (where y, z > 1, and the current number is b = x), then we can add one more coin with demonitaion a > c = x· y > b. So, in the optimal answer sum of degrees decreasing at exactly one. Our greedy algorithm do exactly what it need.
You can prove correctness, if you take a look at prime factorizations of coins' denominations. In each next denomination each prime have less or equal power than the current one (it's equivalent to 'a divide b'). Obliviously, if summary degree of primes decreases at least two (for example, we had numbera = x· y· z (where y, z > 1, and the current number is b = x), then we can add one more coin with demonitaion a > c = x· y > b. So, in the optimal answer sum of degrees decreasing at exactly one. Our greedy algorithm do exactly what it need.
Problem C. Trees.
The first thing we notice - beautiful sequence is can be determined with any member. The next thing - at least one tree will remain the same height. Prove: let's fix height of the first tree, and correct heights of all other ones. Obliviously, they all remain positive.
Solution with work time O(n2): we run down which tree we will fix, determine required height of the first tree and then relax answer.
This solution can be optimized to linear solution: if we don't touch some tree, we know the first element of sequence. Let's count for each possible element amount of trees, which have required height. It can be done with linear loop and the 'increment' operation on array. After that we just find value of the first element, for which amount of 'good' trees is maximal and output n - x, where x is this amount.
Problem D. Calendar
Solution with work time O(n2): we run down which tree we will fix, determine required height of the first tree and then relax answer.
This solution can be optimized to linear solution: if we don't touch some tree, we know the first element of sequence. Let's count for each possible element amount of trees, which have required height. It can be done with linear loop and the 'increment' operation on array. After that we just find value of the first element, for which amount of 'good' trees is maximal and output n - x, where x is this amount.
Problem D. Calendar
We know, that all lines of calendar should have equal length, so we can find this length. It's just 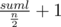 , where suml - summary length of all strings. Now let take a look at string, which will be the first one in our calendar. Obliviously, it's profitably to take string with maximal s + d (where s is our string and d - is character from input). Such string is unique otherwise we have two equal strings in input (as d is not contained in any string); Of cause, you should remember that if you fix the first string in a line, you fix length of the second one - it's required to have at least one such. Great, now we know the first string in our calendar. Now let's determine the second one. We know it's length, so we need just to take minimal string with such length.
, where suml - summary length of all strings. Now let take a look at string, which will be the first one in our calendar. Obliviously, it's profitably to take string with maximal s + d (where s is our string and d - is character from input). Such string is unique otherwise we have two equal strings in input (as d is not contained in any string); Of cause, you should remember that if you fix the first string in a line, you fix length of the second one - it's required to have at least one such. Great, now we know the first string in our calendar. Now let's determine the second one. We know it's length, so we need just to take minimal string with such length.
We know one line, let's do similary with the second line and so on.
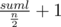 , where suml - summary length of all strings. Now let take a look at string, which will be the first one in our calendar. Obliviously, it's profitably to take string with maximal s + d (where s is our string and d - is character from input). Such string is unique otherwise we have two equal strings in input (as d is not contained in any string); Of cause, you should remember that if you fix the first string in a line, you fix length of the second one - it's required to have at least one such. Great, now we know the first string in our calendar. Now let's determine the second one. We know it's length, so we need just to take minimal string with such length.
, where suml - summary length of all strings. Now let take a look at string, which will be the first one in our calendar. Obliviously, it's profitably to take string with maximal s + d (where s is our string and d - is character from input). Such string is unique otherwise we have two equal strings in input (as d is not contained in any string); Of cause, you should remember that if you fix the first string in a line, you fix length of the second one - it's required to have at least one such. Great, now we know the first string in our calendar. Now let's determine the second one. We know it's length, so we need just to take minimal string with such length.We know one line, let's do similary with the second line and so on.
Problem E. Expression
Under construction. The main idea is 3D dynamic with O(102) transition.










