Пусть $$$T$$$ — дерево из $$$n$$$ вершин. Рассмотрим граф $$$G_0$$$, первоначально равный $$$T$$$. Также есть $$$q$$$ обновлений, где $$$i$$$-е обновление задается парой двух различных целых чисел $$$u_i$$$ и $$$v_i$$$.
Для каждого $$$i$$$ от $$$1$$$ до $$$q$$$ определим граф $$$G_i$$$ следующим образом:
- Если $$$G_{i-1}$$$ содержит ребро $$$\{u_i, v_i\}$$$, то удалите это ребро, чтобы сформировать $$$G_i$$$.
- Иначе добавьте это ребро к $$$G_{i-1}$$$, чтобы сформировать $$$G_i$$$.
Формально, $$$G_i := G_{i-1} \triangle \{\{u_i, v_i\}\}$$$, где $$$\triangle$$$ обозначает симметрическую разность множеств.
Более того, гарантируется, что $$$T$$$ всегда является подграфом $$$G_i$$$. Другими словами, обновление никогда не удаляет ребра из $$$T$$$.
Рассмотрим связный граф $$$H$$$ и запустим в нем поиск в глубину (далее DFS). Можно увидеть, что ребра дерева (то есть ребра, ведущие к еще не посещенной вершине во время обхода) образуют остовное дерево графа $$$H$$$. Это связующее дерево обычно бывает разным для конкретного графа и зависит от начальной вершины и от порядка прохождения соседей каждой вершины.
Назовём вершину $$$w$$$ хорошей, если можно упорядочить соседей каждой вершины таким образом, чтобы DFS, начинающийся в вершине $$$w$$$, давал $$$T$$$ как остовное дерево. Для каждого $$$i$$$ от $$$1$$$ до $$$q$$$ найдите и выведите количество хороших вершин.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$3 \le n \le 2\cdot 10^5$$$, $$$1 \le q \le 2 \cdot 10^5$$$) — количество вершин и обновлений, соответственно.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — вершины, которые соединяет ребро в $$$T$$$. Гарантируется, что этот граф является деревом.
Каждая из следующих $$$q$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — конечные вершины ребра, которое нужно добавить или удалить. Гарантируется, что эти ребра не принадлежат $$$T$$$.
Для каждого обновления, выведите одно целое число $$$k$$$ — количество хороших вершин $$$w$$$ после этого обновления.
3 2
1 2
1 3
2 3
3 2
2
3
6 6
1 2
2 3
1 4
4 5
1 6
2 5
3 4
5 2
6 4
3 4
6 5
3
2
3
2
3
2
Первый пример изображен на следующем рисунке.
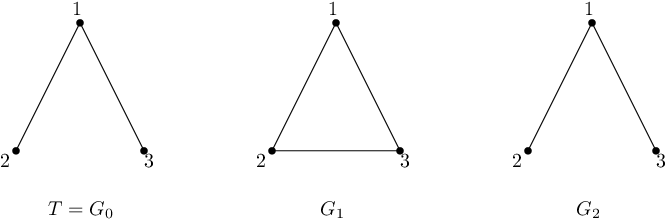
После первого обновления $$$G$$$ содержит все три возможные ребра. Результат DFS'а:
- Начнем в вершине $$$1$$$. Есть два способа как упорядочить соседей вершины $$$1$$$: либо $$$[2, 3]$$$, либо $$$[3, 2]$$$.
- Если мы выберем первый вариант, то мы посетим вершину $$$2$$$. Вне зависимости от порядка его соседей, далее мы посетим вершину $$$3$$$. Таким образом, остовное дерево, сгенерированное этим DFS'ом, будет содержать ребра $$$\{1, 2\}$$$ и $$$\{2, 3\}$$$, которое не равны дереву $$$T$$$.
- Если мы выберем второй вариант, мы получим остовное дерево с ребрами $$$\{1, 3\}$$$ и $$$\{2, 3\}$$$.
- Начнем в вершине $$$2$$$. Есть два способа как упорядочить соседей. Если мы сначала посетим вершину $$$3$$$, то остовное дерево будет состоять из ребер $$$\{2,3\}$$$ и $$$\{1,3\}$$$, которые не равны $$$T$$$. Если мы, однако, посетим сначала $$$1$$$, то мы сможем только перейти в $$$3$$$, и остовное дерево будет состоять из ребер $$$\{1, 2\}$$$ и $$$\{1,3\}$$$, которые равны $$$T$$$. Поэтому, $$$2$$$ является хорошей вершиной.
- Случай, когда мы начинаем в вершине $$$3$$$, симметрично, если бы мы начали в вершине $$$2$$$, и поэтому $$$3$$$ тоже хорошая вершина.
После второго запроса ребро между $$$2$$$ и $$$3$$$ удаляется, и $$$G = T$$$. Из этого следует, что остовное дерево, сгенерированное DFS'ом, всегда будет равно $$$T$$$, вне зависимости от выбора начальной вершины. Поэтому, ответ $$$3$$$.
Во втором примере, множества хороших вершин после каждого запроса:
- $$$\{2, 3, 5\}$$$
- $$$\{3, 5\}$$$
- $$$\{3, 4, 5\}$$$
- $$$\{4, 5\}$$$
- $$$\{4, 5, 6\}$$$
- $$$\{5, 6\}$$$
| Название |
|---|