| Codeforces Global Round 7 |
|---|
| Закончено |
Назовем граф с $$$n$$$ вершинами, каждой из которых соответствует своя точка $$$A_i = (x_i, y_i)$$$ с целыми координатами, планарным деревом, если:
- Все точки $$$A_1, A_2, \ldots, A_n$$$ различны и никакие три точки не лежат на одной прямой.
- Граф является деревом, то есть в графе ровно $$$n-1$$$ ребро и существует путь между любой парой вершин.
- Для всех пар ребер $$$(s_1, f_1)$$$ и $$$(s_2, f_2)$$$, таких что $$$s_1 \neq s_2, s_1 \neq f_2,$$$ $$$f_1 \neq s_2$$$ и $$$f_1 \neq f_2$$$, отрезки $$$A_{s_1} A_{f_1}$$$ и $$$A_{s_2} A_{f_2}$$$ не пересекаются.
Представим планарное дерево на $$$n$$$ вершинах. Рассмотрим выпуклую оболочку множества точек $$$A_1, A_2, \ldots, A_n$$$. Давайте назовем это дерево паутиной если для всех $$$1 \leq i \leq n$$$ следующие условия верны:
- Все листья (вершины со степенью $$$\leq 1$$$) лежат на выпуклой оболочке.
- Все вершины на выпуклой оболочке являются листьями.
Пример паутины:
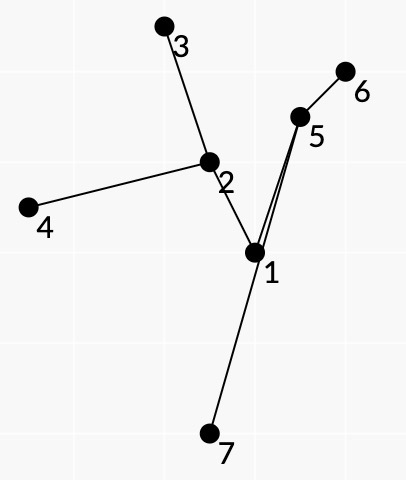
Точки $$$A_3, A_6, A_7, A_4$$$ лежат на выпуклой оболочке и вершины $$$3, 6, 7, 4$$$ это все листья этого дерева.
Обратитесь к примечанию для большего количества примеров.
Давайте назовем подмножество $$$S \subset \{1, 2, \ldots, n\}$$$ вершин поддеревом, если для всех пар вершин из $$$S$$$ существует путь между ними, содержащий только вершины из множества $$$S$$$. Обратите внимание, что любое поддерево планарного дерева также будет являться планарным деревом.
Вам дано планарное дерево, состоящее из $$$n$$$ вершин. Назовем разбиение множества вершин $$$\{1, 2, \ldots, n\}$$$ на непустые подмножества $$$A_1, A_2, \ldots, A_k$$$ (то есть $$$A_i \cap A_j = \emptyset$$$ для всех $$$1 \leq i < j \leq k$$$ и $$$A_1 \cup A_2 \cup \ldots \cup A_k = \{1, 2, \ldots, n\}$$$) хорошим, если для всех $$$1 \leq i \leq k$$$, множество $$$A_i$$$ является поддеревом и паутиной. Два разбиения различны, если существует некоторое множество, лежащее в одном разбиении, но не лежащее в другом.
Найдите количество хороших разбиений. Поскольку это число может быть очень большим, найдите его по модулю $$$998\,244\,353$$$.
В первой строке находится единственное целое число $$$n$$$ ($$$1 \leq n \leq 100$$$) — количество вершин в дереве.
В следующих $$$n$$$ строках находится по два целых числа $$$x_i, y_i$$$ ($$$-10^9 \leq x_i, y_i \leq 10^9$$$) — координаты $$$i$$$-й вершины, точки $$$A_i$$$.
В следующей $$$n-1$$$ строке находится по два целых числа $$$s, f$$$ ($$$1 \leq s, f \leq n$$$) — ребра $$$(s, f)$$$ данного дерева.
Гарантируется, что все точки различны и никакие три точки не лежат на одной прямой. Также гарантируется, что данные ребра и координаты точек описывают планарное дерево.
Выведите одно целое число — количество хороших разбиений множества вершин данного планарного дерева по модулю $$$998\,244\,353$$$.
4 0 0 0 1 -1 -1 1 -1 1 2 1 3 1 4
5
5 3 2 0 -3 -5 -3 5 -5 4 5 4 2 4 1 5 2 2 3
8
6 4 -5 0 1 -2 8 3 -10 0 -1 -4 -5 2 5 3 2 1 2 4 6 4 2
13
8 0 0 -1 2 -2 5 -5 1 1 3 0 3 2 4 -1 -4 1 2 3 2 5 6 4 2 1 5 5 7 5 8
36
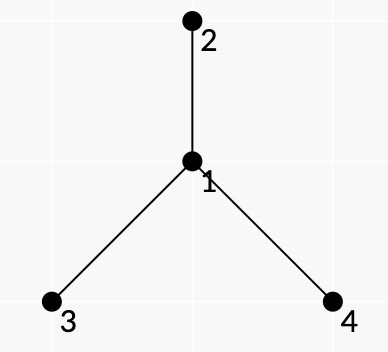Картинка дерева из первого теста. В первом тесте, все хорошие разбиения это:
- $$$\{1\}$$$, $$$\{2\}$$$, $$$\{3\}$$$, $$$\{4\}$$$;
- $$$\{1, 2\}$$$, $$$\{3\}$$$, $$$\{4\}$$$;
- $$$\{1, 3\}$$$, $$$\{2\}$$$, $$$\{4\}$$$;
- $$$\{1, 4\}$$$, $$$\{2\}$$$, $$$\{3\}$$$;
- $$$\{1, 2, 3, 4\}$$$.
Разбиение $$$\{1, 2, 3\}$$$, $$$\{4\}$$$ не является хорошим, потому что поддерево $$$\{1, 2, 3\}$$$ это не паутина, потому что вершина $$$1$$$, не являющаяся листом, лежит на выпуклой оболочке.
Разбиение $$$\{2, 3, 4\}$$$, $$$\{1\}$$$ не является хорошим, потому что подмножество $$$\{2, 3, 4\}$$$ не является поддеревом.
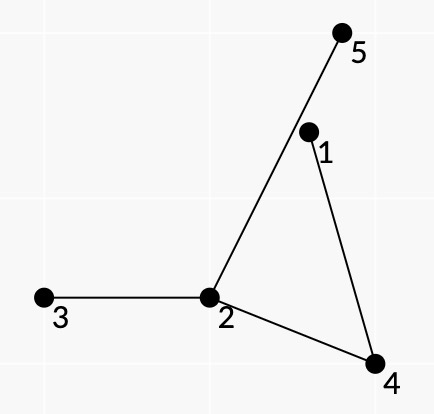Картинка дерева из второго теста. Во втором тесте, данное дерево само не является паутиной, потому что вершина $$$1$$$, которая является листом, не лежит на выпуклой оболочке. Однако, поддерево $$$\{2, 3, 4, 5\}$$$ является паутиной.
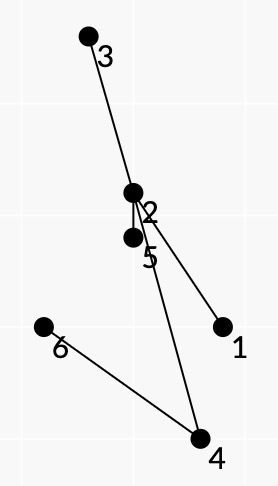Картинка дерева из третьего теста. 
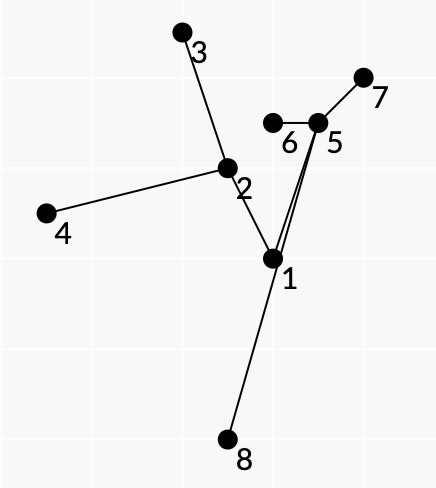Картинка дерева из четвертого теста. В четвертом тесте, разбиение $$$\{1, 2, 3, 4\}$$$, $$$\{5, 6, 7, 8\}$$$ хорошее, потому что оба подмножества являются паутинами.
