This is the easy version of the problem. The only difference is that in this version $$$q=1$$$. You can make hacks only if all versions of the problem are solved.
Zookeeper has been teaching his $$$q$$$ sheep how to write and how to add. The $$$i$$$-th sheep has to write exactly $$$k$$$ non-negative integers with the sum $$$n_i$$$.
Strangely, sheep have superstitions about digits and believe that the digits $$$3$$$, $$$6$$$, and $$$9$$$ are lucky. To them, the fortune of a number depends on the decimal representation of the number; the fortune of a number is equal to the sum of fortunes of its digits, and the fortune of a digit depends on its value and position and can be described by the following table. For example, the number $$$319$$$ has fortune $$$F_{2} + 3F_{0}$$$.
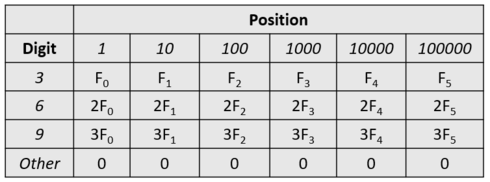
Each sheep wants to maximize the sum of fortune among all its $$$k$$$ written integers. Can you help them?
The first line contains a single integer $$$k$$$ ($$$1 \leq k \leq 999999$$$): the number of numbers each sheep has to write.
The next line contains six integers $$$F_0$$$, $$$F_1$$$, $$$F_2$$$, $$$F_3$$$, $$$F_4$$$, $$$F_5$$$ ($$$1 \leq F_i \leq 10^9$$$): the fortune assigned to each digit.
The next line contains a single integer $$$q$$$ ($$$q = 1$$$): the number of sheep.
Each of the next $$$q$$$ lines contains a single integer $$$n_i$$$ ($$$1 \leq n_i \leq 999999$$$): the sum of numbers that $$$i$$$-th sheep has to write. In this version, there is only one line.
Print $$$q$$$ lines, where the $$$i$$$-th line contains the maximum sum of fortune of all numbers of the $$$i$$$-th sheep. In this version, you should print only one line.
3 1 2 3 4 5 6 1 57
11
3 1 2 3 4 5 6 1 63
8
In the first test case, $$$57 = 9 + 9 + 39$$$. The three $$$9$$$'s contribute $$$1 \cdot 3$$$ and $$$3$$$ at the tens position contributes $$$2 \cdot 1$$$. Hence the sum of fortune is $$$11$$$.
In the second test case, $$$63 = 35 + 19 + 9$$$. The sum of fortune is $$$8$$$.
| Name |
|---|




