| Codeforces Global Round 13 |
|---|
| Finished |
There is a graph of $$$n$$$ rows and $$$10^6 + 2$$$ columns, where rows are numbered from $$$1$$$ to $$$n$$$ and columns from $$$0$$$ to $$$10^6 + 1$$$:
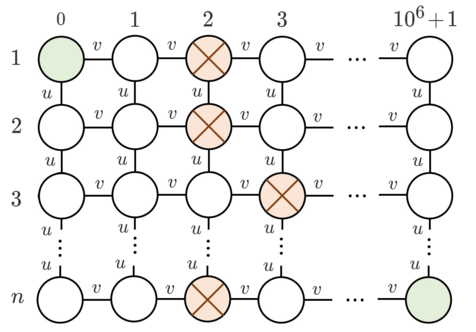
Let's denote the node in the row $$$i$$$ and column $$$j$$$ by $$$(i, j)$$$.
Initially for each $$$i$$$ the $$$i$$$-th row has exactly one obstacle — at node $$$(i, a_i)$$$. You want to move some obstacles so that you can reach node $$$(n, 10^6+1)$$$ from node $$$(1, 0)$$$ by moving through edges of this graph (you can't pass through obstacles). Moving one obstacle to an adjacent by edge free node costs $$$u$$$ or $$$v$$$ coins, as below:
- If there is an obstacle in the node $$$(i, j)$$$, you can use $$$u$$$ coins to move it to $$$(i-1, j)$$$ or $$$(i+1, j)$$$, if such node exists and if there is no obstacle in that node currently.
- If there is an obstacle in the node $$$(i, j)$$$, you can use $$$v$$$ coins to move it to $$$(i, j-1)$$$ or $$$(i, j+1)$$$, if such node exists and if there is no obstacle in that node currently.
- Note that you can't move obstacles outside the grid. For example, you can't move an obstacle from $$$(1,1)$$$ to $$$(0,1)$$$.
Refer to the picture above for a better understanding.
Now you need to calculate the minimal number of coins you need to spend to be able to reach node $$$(n, 10^6+1)$$$ from node $$$(1, 0)$$$ by moving through edges of this graph without passing through obstacles.
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 10^4$$$) — the number of test cases.
The first line of each test case contains three integers $$$n$$$, $$$u$$$ and $$$v$$$ ($$$2 \le n \le 100$$$, $$$1 \le u, v \le 10^9$$$) — the number of rows in the graph and the numbers of coins needed to move vertically and horizontally respectively.
The second line of each test case contains $$$n$$$ integers $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^6$$$) — where $$$a_i$$$ represents that the obstacle in the $$$i$$$-th row is in node $$$(i, a_i)$$$.
It's guaranteed that the sum of $$$n$$$ over all test cases doesn't exceed $$$2 \cdot 10^4$$$.
For each test case, output a single integer — the minimal number of coins you need to spend to be able to reach node $$$(n, 10^6+1)$$$ from node $$$(1, 0)$$$ by moving through edges of this graph without passing through obstacles.
It can be shown that under the constraints of the problem there is always a way to make such a trip possible.
3 2 3 4 2 2 2 3 4 3 2 2 4 3 3 2
7 3 3
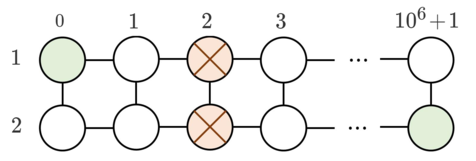
In the first sample, two obstacles are at $$$(1, 2)$$$ and $$$(2,2)$$$. You can move the obstacle on $$$(2, 2)$$$ to $$$(2, 3)$$$, then to $$$(1, 3)$$$. The total cost is $$$u+v = 7$$$ coins.
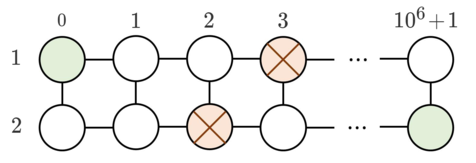
In the second sample, two obstacles are at $$$(1, 3)$$$ and $$$(2,2)$$$. You can move the obstacle on $$$(1, 3)$$$ to $$$(2, 3)$$$. The cost is $$$u = 3$$$ coins.
| Name |
|---|




