1491A - K-th Largest Value
Setter: syksykCCC
Prepared by: syksykCCC
How can we find the largest $$$k$$$ such that the $$$k$$$-th smallest element of the array is $$$0$$$?
How can we maintain $$$k$$$?
Let's define $$$cnt$$$ to represent the number of 1s in the array.
For the modifications, if $$$a_i$$$ is already $$$1$$$ now, then we let $$$cnt \gets cnt - 1$$$. Otherwise, let $$$cnt \gets cnt + 1$$$.
For the querys, just compare $$$cnt$$$ with $$$k$$$. If $$$cnt \ge k$$$, the answer will be $$$1$$$. Otherwise, the answer will be $$$0$$$.
The complexity : $$$O(n + q)$$$.
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, q, a[N], cnt;
int main()
{
scanf("%d%d",&n,&q);
for(int i = 1; i <= n; ++i)
{
scanf("%d",a+i);
cnt += a[i];
}
while(q--)
{
int opt, x;
scanf("%d%d",&opt,&x);
if(opt == 1)
{
if(a[x]) cnt--;
else cnt++;
a[x] = 1 - a[x];
}
else
{
if(cnt >= x) puts("1");
else puts("0");
}
}
return 0;
}
n, q = map(int,input().split())
a = list(map(int,input().split()))
zero = a.count(0)
one = n - zero
for _ in range(q):
t, x = map(int,input().split())
if t == 1:
if a[x-1] == 1:
zero += 1
one -= 1
a[x-1] = 0
else:
zero -= 1
one += 1
a[x-1] = 1
else:
if x<=one:
print(1)
else:
print(0)
1491B - Minimal Cost
Setter: syksykCCC
Prepared by: syksykCCC
When is the answer $$$0$$$? Or rather, when do you not have to make any moves?
What happens if $$$a[i]$$$ is same for all $$$i$$$?
Consider the following situations:
- $$$\forall i \in [2,n], |a_i - a_{i - 1}| = 0$$$, then the answer will be $$$v + \min(u, v)$$$.
- $$$\exists i \in [2,n], |a_i - a_{i - 1}| > 1$$$, then the answer will be $$$0$$$.
- Otherwise, the answer will be $$$\min(u, v)$$$.
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, a[N], ans = INT_MAX, u, v, T;
int main()
{
ios::sync_with_stdio(false);
cin>>T;
while(T--){
ans = INT_MAX;
cin >> n >> u >> v;
for(int i = 1; i <= n; i++)
cin >> a[i];
for(int i = 2; i <= n; i++)
{
if(abs(a[i] - a[i - 1]) >= 2) ans = 0;
if(abs(a[i] - a[i - 1]) == 1) ans = min(ans, min(u, v));
if(a[i] == a[i - 1]) ans = min(ans, v + min(u, v));
}
cout << ans << endl;
}
return 0;
}
1491C - Pekora and Trampoline
Setter: oolimry
Prepared by: errorgorn
Think greedily!
By exchange argument, where can Pekora start her pass in an optimal solution?
For a series of passes, we can describe it as an array $$$P$$$ where $$$P_i$$$ is the trampoline Pekora starts at in the $$$i$$$-th pass. We claim that the final state of trampolines after performing any permutation of $$$P$$$ will be the same.
Focus on $$$2$$$ adjacent passes. We realize that if we swap those $$$2$$$ passes, the jumps done on both these passes are the same.
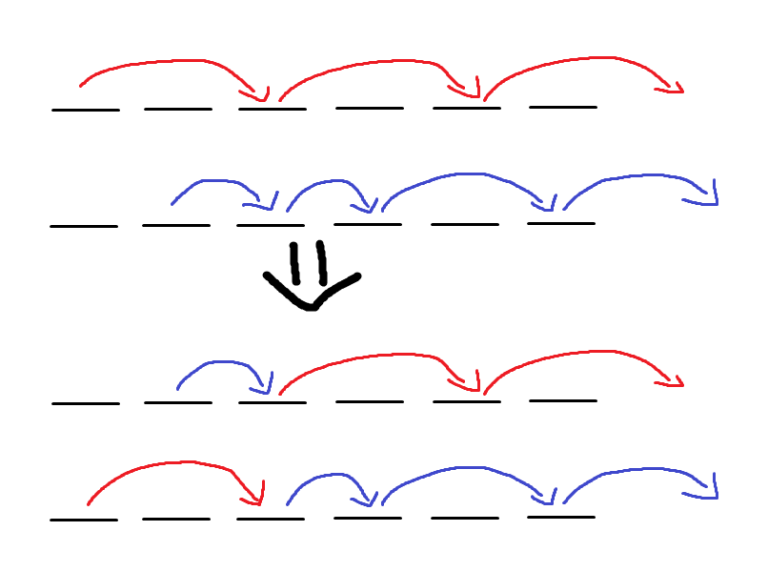
Since swapping any $$$2$$$ adjacent passes does not change the final state of trampolines, any permutation of $$$P$$$ will not change the final state of trampolines.
Now, we can claim that there is an optimal solution with $$$P$$$ being non-decreasing. Since Pekora can only move right, we must put Pekora on the first trampoline such that $$$S_i \ne 1$$$.
However, we cannot directly simulate putting Pekora on the first trampoline such that $$$S_i \ne 1$$$. This actually uses $$$O(N^3)$$$.
5000 4999 4998 4997 ... 2 1
However, we can simulate this in $$$O(N^2)$$$ by the following. Instead of simulating passes individually, we will combine them. The main idea is that when Pekora jumps on a trampoline of strength $$$S_i$$$, we just add another Pekora on trampoline $$$S_i+i$$$ and process it later.
So, when we process trampolines from $$$1$$$ to $$$N$$$, we keep track of how many Pekoras there are on trampoline $$$i$$$, which we will denote as $$$C_i$$$. Then, we only add extra Pekoras to trampoline $$$i$$$ if $$$S_i>C_i+1$$$. Now, we have some Pekoras on trampoline $$$i$$$ and we need to update other values of $$$C_i$$$.
If $$$S_i=4$$$ and $$$C_i=6$$$ for example, we would add $$$1$$$ Pekora each trampolines to $$$i+2,i+3,i+4$$$ to reduce $$$S_i$$$ to 1. Then, the rest of the Pekoras will be moved to trampoline $$$i+1$$$.
This algorithm runs in $$$O(N^2)$$$ as we only need to update $$$O(N)$$$ other trampolines at each step.
Bonus: solve this problem in $$$O(N)$$$. (This was the original constraints but it was later changed since it was too hard for its position.)
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define up upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n;
int arr[5005];
ll curr[5005];
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
cin>>n;
rep(x,0,n) cin>>arr[x];
rep(x,0,n) curr[x]=0;
ll ans=0;
rep(x,0,n){
ll temp=curr[x];
if (temp<arr[x]-1){
ans+=arr[x]-1-temp;
temp+=arr[x]-1-temp;
}
curr[x+1]+=temp-arr[x]+1;
if (x+2<n) rep(y,x+2,min(n,x+arr[x]+1)) curr[y]++;
}
cout<<ans<<endl;
}
}
TC=int(input())
for tc in range(TC):
n=int(input())
arr=list(map(int,input().split()))
curr=[0]*(n+5)
ans=0
for x in range(n):
temp=curr[x]
if (temp<arr[x]-1):
ans+=arr[x]-1-temp
temp+=arr[x]-1-temp
curr[x+1]+=temp-arr[x]+1
for y in range(x+2,min(n,x+arr[x]+1)):
curr[y]+=1
print(ans)
1491D - Zookeeper and The Infinite Zoo
Setter: errorgorn
Prepared by: errorgorn
Since $$$\&$$$ is a bitwise operation, represent the number in binary form!
We can convert any $$$u+v$$$ move to a series of $$$u+v'$$$ moves where $$$u\&v'=v'$$$ and $$$v'=2^k$$$.
Such a move converts a substring of the binary string of the form $$$01\ldots11$$$ into $$$10\ldots00$$$.
Focus on converting $$$01$$$ into $$$10$$$.
Firstly, we can show that the reachability graph is equivalent if we restrict to a directed edge between vertices $$$u$$$ and $$$u+v$$$ if $$$u\&v=v$$$ and that $$$v=2^k$$$ for some $$$k$$$.
This is because we can add each bit from $$$v$$$ from $$$u$$$ from the highest bit as adding a bit to a number will not affect lower bits.
Now, we observe that such as operation converts a binary string of the form $$$01\ldots11$$$ into $$$10\ldots00$$$ for some substring when we represent $$$u$$$ as a binary string. (more significant bits are to the left).
Now, we consider $$$s$$$ and $$$t$$$ as binary strings.
If and only if there is a matching from bits in $$$t$$$ to a lower bit in $$$s$$$ and $$$t$$$ > $$$s$$$, then $$$t$$$ is reachable from $$$s$$$.
Turning $$$01\ldots11$$$ into $$$10\ldots00$$$ means that we can move a bit ($$$01$$$->$$$10$$$) or we can squish multiple bits ($$$0111$$$->$$$1000$$$).
Let us show it is necessary. If $$$s>t$$$, it is impossible. And if there is no such matching, we are not able to put a position in $$$t$$$ as bits cannot move back, or there are not enough bits in $$$s$$$ to form $$$t$$$ (since the number of bits cannot increase).
Let is show it is sufficient. Since $$$s<t$$$ ($$$s=t$$$ is trivial), the strings have some common prefix and the most significant different bit has $$$0$$$ in $$$s$$$ and $$$1$$$ and $$$t$$$. Now, we can shift every bit in s into a position in t and squish the most significant bits.
To check if there is a matching, we find the least significant bit ($$$lsb$$$) of $$$t$$$ and $$$s$$$. if $$$lsb(t) < lsb(s)$$$ or if $$$s = 0$$$, then it is impossible. Else, we remove the $$$lsb$$$ from both $$$t$$$ and $$$s$$$ and repeat. If we're able to remove bits until $$$t=0$$$, then it is possible to go from $$$s$$$ to $$$t$$$.
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define up upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
int TC;
cin>>TC;
while (TC--){
int a,b;
cin>>a>>b;
vector<int> va,vb;
if (a>b){
cout<<"NO"<<endl;
goto done;
}
rep(x,0,30){
if (a&(1<<x)) va.pub(x);
if (b&(1<<x)) vb.pub(x);
}
if (sz(va)<sz(vb)){
cout<<"NO"<<endl;
goto done;
}
rep(x,0,sz(vb)){
if (va[x]>vb[x]){
cout<<"NO"<<endl;
goto done;
}
}
cout<<"YES"<<endl;
done:;
}
}
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int t;cin >> t;
while(t--){
int x,y;cin >> x >> y;
int z=0;
bool ok=(x<=y);
for(int i=0; i<30 ;i++){
if((x>>i)&1) z++;
if((y>>i)&1) z--;
if(z<0) ok=false;
}
if(ok) cout << "YES\n";
else cout << "NO\n";
}
}
def lsb(x):
return x & (-x)
Q = int(input())
for q in range(Q):
a,b = map(int,input().split(" "))
if a > b:
print("NO")
else:
can = True
while b > 0:
if lsb(b) < lsb(a) or a == 0:
can = False
break
a -= lsb(a)
b -= lsb(b)
print("YES" if can else "NO")
1491E - Fib-tree
Setter: Widowmaker
Prepared by: Widowmaker and syksykCCC
The only pair $$$(j,k)$$$ that satisfies $$$F_i=F_j+F_k$$$ is $$$(i-1,i-2)$$$.
Firstly, we can discover that we can only cut a tree in the size of $$$f_{i}$$$ into one in size of $$$f_{i-1}$$$ and one in size of $$$f_{i-2}$$$.
We want to show that the only solution to $$$F_i=F_j+F_k$$$ is $$$(j,k)=(i-1,i-2)$$$ for $$$j \geq k$$$.
Clearly, $$$i>j$$$, otherwise, $$$F_i<F_j+F_k$$$.
Furthermore, $$$j>i-2$$$ as $$$F_i>2 \cdot F_{i-2}$$$.
Therefore, we have shown the only solution is $$$(j,k)=(i-1,i-2)$$$.
However, we will have 2 ways to partition the tree sometimes. But it turns out we can cut any edge!
We will prove that if some edge cuts Fib-tree of $$$F_n$$$ vertices into trees with sizes $$$F_{n-1}$$$ and $$$F_{n-2}$$$, we can cut it, and the resulting trees are also Fib-trees.
By induction. For $$$n = 2$$$ it's obvious.
If only edge cuts Fib-tree into trees with sizes $$$F_{n-1}$$$ and $$$F_{n-2}$$$, we have to cut it.
If there are two such edges: suppose that cutting the first edge results in making two Fib-trees. Then in the tree of size $$$F_{n-1}$$$ the second edge divides it into trees of sizes $$$F_{n-2}$$$ and $$$F_{n-3}$$$, so we can cut it as well in the next step. But then we could as well cut the second edge first: we will have one Fib-tree of size $$$F_{n-2}$$$, and one tree of size $$$F_{n-1}$$$ which is cut into Fib-trees of sizes $$$F_{n-2}$$$ and $$$F_{n-3}$$$ by the first edge, so it's also a Fib-tree!
Because the growth of Fibonacci sequence is approximately $$$O(\phi^n)$$$, we only need to cut our tree $$$O(\log_\phi n)$$$ times: every time, if we find the splitting edge, we cut it, and recurse to the resulting trees, if at some point there was no splitting edge — tree isn't Fib-tree.
Finally, we got an $$$O(n\log_\phi n)$$$ solution.
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int n, siz[N];
vector<int> fib;
vector<pair<int, bool> > G[N];
void NO() { cout << "NO\n"; exit(0); }
void GetSize(int u, int fa)
{
siz[u] = 1;
for(pair<int, bool> e : G[u])
{
if(e.second) continue;
int v = e.first;
if(v == fa) continue;
GetSize(v, u);
siz[u] += siz[v];
}
}
void CutEdge(int u, int fa, int k, int &pu, int &pv, int &kd)
{
for(pair<int, bool> e : G[u])
{
if(pu) return;
if(e.second) continue;
int v = e.first;
if(v == fa) continue;
if(siz[v] == fib[k - 1] || siz[v] == fib[k - 2])
{
pu = u; pv = v;
kd = (siz[v] == fib[k - 1]) ? k - 1 : k - 2;
break;
}
CutEdge(v, u, k, pu, pv, kd);
}
}
void Check(int u, int k)
{
// cout << "Check " << u << ' ' << k << endl;
if(k <= 1) return;
GetSize(u, 0);
int pu = 0, pv = 0, kd = 0;
CutEdge(u, 0, k, pu, pv, kd);
// cout << pu << ' ' << pv << ' ' << kd << endl;
if(!pu) NO();
for(pair<int, bool> &e : G[pu])
if(e.first == pv) e.second = true;
for(pair<int, bool> &e : G[pv])
if(e.first == pu) e.second = true;
Check(pv, kd);
Check(pu, (kd == k - 1) ? k - 2 : k - 1);
}
int main()
{
ios::sync_with_stdio(false);
cin >> n;
fib.push_back(1);
fib.push_back(1);
for(int i = 1; ; i++)
{
if(fib[i] >= n) break;
int new_fib = fib[i] + fib[i - 1];
fib.push_back(new_fib);
}
for(int i = 1; i < n; i++)
{
int u, v;
cin >> u >> v;
G[u].push_back(make_pair(v, false));
G[v].push_back(make_pair(u, false));
}
if(fib[fib.size() - 1] != n) NO();
Check(1, fib.size() - 1);
cout << "YES\n";
return 0;
}
1491F - Magnets
Setter: 3.141592653 and star_xingchen_c
Prepared by: 3.141592653 and star_xingchen_c
Try to construct a solution that works in $$$2n$$$ queries.
Try to find the second magnet which is not `-'.
The actual query limit is $$$n-1+\lceil\log_2n\rceil$$$.
It seems this problem needs some random technique, but here is a determinate solution:
We just try to find a not demagnetized magnet.
You can go through the following method to find one:
First put the first magnet in the left.
Then ask all the other magnets with the left pile.
If we got a non-zero answer, we find a valid magnet; else we just put this magnet in the left.
It can be proven later that we will always be able to find a valid magnet.
Then use this magnet to try on all other magnets.
This process form a solution requiring at most $$$2n-2$$$ queries.
However, when we look back at this solution we'll realize that there is a huge waste of information in the previous queries.
As all the previous answers are $$$0$$$, it's easy to prove that the magnet we found is the second one we have selected.
Since we know nothing about the right part, we can simply check the magnets in the right one by one.
However, you have known that there is only $$$1$$$ magnetic magnet in the left, so you can do a binary search to seek for the answer.
The maximum number of queries is $$$n-1+\lceil\log_2n\rceil$$$, which perfectly matches the limit.
#include<bits/stdc++.h>
int n;
std::vector<int>ans,tmp,hlf;
int main()
{
int T;
scanf("%d",&T);
for(;T--;)
{
ans.clear(),tmp.clear(),hlf.clear();
scanf("%d",&n);
register int i,ii;
int sec=0;
for(i=2;i<=n;i++)
{
printf("? 1 %d\n%d\n",i-1,i);
for(ii=1;ii<i;ii++)printf("%d ",ii);
puts(""),fflush(stdout);
int f;
scanf("%d",&f);
if(f){sec=i;break;}
}for(i=sec+1;i<=n;i++)
{
printf("? 1 1\n%d\n%d\n",sec,i);
fflush(stdout);
int f;
scanf("%d",&f);
if(!f)ans.push_back(i);
}for(i=1;i<sec;i++)tmp.push_back(i);
while(tmp.size()>1)
{
int md=tmp.size()>>1;
hlf.clear();
for(i=1;i<=md;i++)
hlf.push_back(tmp.back()),tmp.pop_back();
printf("? 1 %d\n%d\n",md,sec);
for(int t:hlf)printf("%d ",t);
puts(""),fflush(stdout);
int f;
scanf("%d",&f);
if(f)tmp=hlf;
}
for(i=1;i<sec;i++)if(tmp[0]!=i)ans.push_back(i);
printf("! %u",ans.size());
for(int t:ans)printf(" %d",t);
puts(""),fflush(stdout);
}
}
1491G - Switch and Flip
Setter: errorgorn and oolimry
Prepared by: errorgorn
Visualize this problem as graph with directed edges $$$(i,c_i)$$$.
Solve this problem where there is only $$$1$$$ big cycle.
What if a cycle has $$$2$$$ coins that are upside down? How can we force a cycle into such state?
We can visualize the problem as a graph with nodes of $$$2$$$ colors (face up — red and face down — blue). Initially, the graph has nodes with all red color and with a directed edge to $$$c_i$$$.
Firstly, any $$$2$$$ cycles with all red nodes can be converted into a single cycle with $$$2$$$ blues nodes with $$$1$$$ swap.
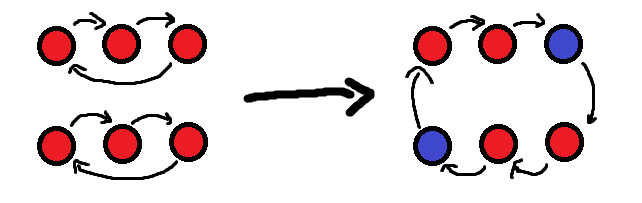
A cycle with $$$2$$$ blue nodes is very convenient here as swapping a blue node with a red node it is pointing to will decrease the cycle size and maintain that the cycle still has $$$2$$$ blue nodes. We can keep decreasing the cycle size until the cycle has only $$$2$$$ blue nodes and solve that in $$$1$$$ swap. Thus, solving $$$2$$$ cycles which have $$$X$$$ nodes in total uses only $$$X$$$ swaps.
Now, we simply pair the cycles and do this.
However, if there is an odd number of cycles, there are $$$2$$$ cases:
If the cycle does not cover the whole graph, we can solve the remaining cycle and a cycle of size $$$1$$$ together.
Otherwise, we can force $$$2$$$ blue nodes into the cycle with $$$2$$$ swaps (does not work for $$$n = 2$$$ so be careful).
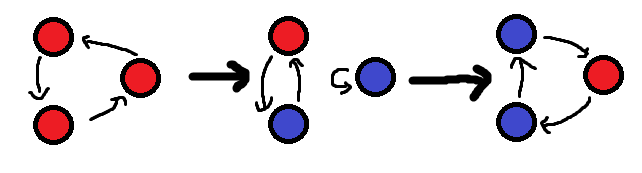
Both cases need $$$X+1$$$ moves where $$$X$$$ is the size of the remaining cycle.
Thus, at most $$$X+1$$$ swaps is needed in this algorithm.
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define up upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n;
int arr[200005];
bool vis[200005];
vector<ii> ans;
void cswap(int i,int j){
swap(arr[i],arr[j]);
arr[i]=-arr[i],arr[j]=-arr[j];
ans.pub(ii(i,j));
}
void swap_cyc(int i,int j){
cswap(i,j);
int curr=i;
while (arr[-arr[curr]]>0){
cswap(curr,-arr[curr]);
}
curr=-arr[curr];
while (arr[-arr[curr]]>0){
cswap(curr,-arr[curr]);
}
cswap(curr,-arr[curr]);
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n;
rep(x,1,n+1) cin>>arr[x];
int p=-1;
rep(x,1,n+1) if (!vis[x]){
if (arr[x]==x) continue;
int curr=x;
do{
vis[curr]=true;
curr=arr[curr];
} while (curr!=x);
if (p==-1) p=x;
else{
swap_cyc(p,x);
p=-1;
}
}
if (p!=-1){
bool can=false;
rep(x,1,n+1) if (arr[x]==x){
swap_cyc(p,x);
can=true;
break;
}
if (!can){
int t1=arr[p],t2=arr[arr[p]];
cswap(p,t1);
swap_cyc(t1,t2);
}
}
cout<<sz(ans)<<endl;
for (auto &it:ans) cout<<it.fi<<" "<<it.se<<endl;
}
from sys import stdin, stdout
n=int(stdin.readline())
#make 1-indexed
arr=[0]+list(map(int,stdin.readline().split()))
vis=[0]*(n+1)
ans=[]
def cswap(i,j):
arr[i],arr[j]=-arr[j],-arr[i]
ans.append((i,j))
def swap_cyc(i,j):
cswap(i,j)
curr=i
while (arr[-arr[curr]]>0):
cswap(curr,-arr[curr])
curr=-arr[curr]
while (arr[-arr[curr]]>0):
cswap(curr,-arr[curr])
cswap(curr,-arr[curr])
p=-1
for i in range(1,n+1):
if (vis[i]==1): continue
if (arr[i]==i): continue
curr=i
while (True):
vis[curr]=1
curr=arr[curr]
if (curr==i): break
if (p==-1):
p=i
else:
swap_cyc(p,i)
p=-1
if (p!=-1):
can=False
for i in range(1,n+1):
if (arr[i]==i):
swap_cyc(p,i)
can=True
break
if (can==False):
t1,t2=arr[p],arr[arr[p]]
cswap(p,t1)
swap_cyc(t1,t2)
print(len(ans))
[print(i[0],i[1]) for i in ans]
1491H - Yuezheng Ling and Dynamic Tree
Setter: Ynoi
Prepared by: Widowmaker and Ynoi
The complexity is $$$\mathcal O(n\sqrt{n})$$$.
Divide the nodes into $$$\sqrt{n}$$$ blocks. The $$$i$$$-th block will contain the nodes in $$$[(i-1) \sqrt{n}+1,i \sqrt{n}]$$$.
Let's define $$$f_x$$$ as an ancestor of $$$x$$$ such that $$$f_x$$$ is in the same block as $$$x$$$ and $$$a_{f_x}$$$ is not in the same block as $$$x$$$.
Notice that for a given block, if all $$$a_x$$$ is not in the same block as $$$x$$$, then $$$f_x=x$$$.
So, we do not have to re-compute all values of $$$f_x$$$ for a certain block if $$$\forall x, x-a_x \geq \sqrt n$$$ in this block.
When we update a range, we will update some ranges fully and update at most $$$2$$$ ranges partially. Let's show that only $$$O(n+q)$$$ re-computations will happen.
For a certain block, if it is completely contained in an update, the value of $$$x-a_x$$$ will increase by $$$1$$$, a single block will be re-computed by at most $$$O(\sqrt n)$$$ of such updates, which will contribute $$$O(\sqrt n \cdot \sqrt n)=O(n)$$$ re-computations.
For blocks that are partially updated by an update, such things will only happen at most $$$2q$$$ times, therefore we have a bound of $$$O(q)$$$ re-computations from such updates.
Maintaining $$$f_x$$$, querying can be easily done in $$$O(\sqrt n)$$$.
#include <bits/stdc++.h>
#define N 100005
using namespace std;
template <typename T>
void read(T &a)
{
T x = 0,f = 1;
char ch = getchar();
while (ch < '0' || ch > '9')
{
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9')
{
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
a = x * f;
}
template <typename T>
void write(T x)
{
if (x < 0) putchar('-'),x = -x;
if (x < 10) return (void) putchar(x + '0');
write(x / 10);
putchar(x % 10 + '0');
}
template <typename T>
void writeln(T x)
{
write(x);
putchar('\n');
}
template <typename T>
void writes(T x)
{
write(x);
putchar(' ');
}
template <typename T,typename... Args>
void read(T &maxx,Args &... args)
{
read(maxx);
read(args...);
}
template <typename T,typename... Args>
void writeln(T maxx,Args ... args)
{
writes(maxx);
writes(args...);
putchar('\n');
}
const int B = 300;
int n,q,a[N],num,bl[N],vis[N];
std::vector<int> v;
struct Block
{
int f[B],lazy,flag,cnt,L,R;
void update()
{
flag = 1;
for (int i = L; i <= R; i++)
{
if (bl[i] != bl[a[i]]) f[i - L] = i;
else f[i - L] = f[a[i] - L],flag = 0;
}
}
void update(int l,int r,int x)
{
for (int i = l; i <= r; i++)
a[i] = i == 1 ? 0 : max(a[i] - x,1);
update();
}
void update(int x)
{
if (flag) lazy += x;
else update(L,R,x);
}
}T[(N - 1) / B + 5];
void update(int l,int r,int x)
{
if (bl[l] == bl[r])
{
T[bl[l]].update(l,r,x);
return ;
}
T[bl[l]].update(l,T[bl[l]].R,x);
for (int i = bl[l] + 1; i < bl[r]; i++)
T[i].update(x);
T[bl[r]].update(T[bl[r]].L,r,x);
// cout << l << ' ' << r << ' ' << x << endl;
// cout << '0' << ' ';
// for (int i = 2; i <= n; i++)
// cout << max(a[i] - T[bl[i]].lazy,1) << ' ';
// cout << endl;
}
void clear()
{
for (int i = 0; i < v.size(); i++)
vis[v[i]] = 0;
v.clear();
}
int query(int x,int y)
{
// cout << '0' << ' ';
// for (int i = 2; i <= n; i++)
// cout << max(a[i] - T[bl[i]].lazy,1) << ' ';
// cout << endl;
while (T[bl[x]].f[x - T[bl[x]].L] != T[bl[y]].f[y - T[bl[y]].L])
{
if (bl[x] < bl[y]) swap(x,y);
// cout << x << ' ' << T[bl[x]].f[x - T[bl[x]].L] << endl;
x = (T[bl[x]].f[x - T[bl[x]].L] == 1) ? 0 : max(a[T[bl[x]].f[x - T[bl[x]].L]] - T[bl[x]].lazy,1);
}
int qaq = (T[bl[x]].f[x - T[bl[x]].L] == 1) ? 0 : max(a[T[bl[x]].f[x - T[bl[x]].L]] - T[bl[x]].lazy,1);
while (x != qaq)
{
assert(x != qaq);
vis[x] = 1;
v.push_back(x);
x = (x == 1) ? 0 : max(a[x] - T[bl[x]].lazy,1);
}
while (y != qaq)
{
if (vis[y]) return clear(),y;
y = (y == 1) ? 0 : max(a[y] - T[bl[y]].lazy,1);
}
}
signed main()
{
read(n,q);
for (int i = 2; i <= n; i++) read(a[i]);
num = (n - 1) / B + 1;
for (int i = 1; i <= num; i++)
{
T[i].L = (i - 1) * B + 1;
T[i].R = min(i * B,n);
T[i].cnt = i * B - (i - 1) * B;
T[i].flag = T[i].lazy = 0;
for (int j = T[i].L; j <= T[i].R; j++)
bl[j] = i;
}
for (int i = 1; i <= num; i++)
T[i].update();
while (q--)
{
int opt;
read(opt);
if (opt == 1)
{
int l,r,x;
read(l,r,x);
update(l,r,x);
}
if (opt == 2)
{
int u,v;
read(u,v);
writeln(query(u,v));
}
}
// cerr << (double) clock() / CLOCKS_PER_SEC << endl;
return 0;
}
1491I - Ruler Of The Zoo
Setter: oolimry
Prepared by: oolimry
As the solution to this problem is very long, the full editorial is split into $$$4$$$ parts. If you want to challenge yourself, you can try reading one part at a time and see if you get any inspiration. You can also try to read the specific hints for each part.
Convert the queue into a circle.
Firstly, let's convert the queue into a circle. In our new problem, $$$n$$$ animals stand in a circle. The king fights the animal directly clockwise to it. If the king wins, he and the other person swap places, otherwise nothing happens. The animal that is king will always move 1 space clockwise regardless of what happens.

For example, in this scenario, 0 beats 1, so he stays as king. But he then loses to 2.
Call animals whose A is smaller than the B of the animal before them RED color and the rest of the animals NONRED color.
Work out the inequalities.
How do the colors of animals change?
Let's give each animal a color. An animal $$$i$$$ is RED if $$$B_{i-1}$$$ > $$$A_i$$$. In other words, and animal is red if and only if the previous animal will beat it as king. The animals that are not red are called NONRED for now.
We can assume no two animals are consecutively RED* (*will elaborate more in part 4). Suppose we have 3 animals $$$XYZ$$$ in that order, and $$$Y$$$ is red while $$$X$$$ and $$$Z$$$ are non-red. Suppose $$$X$$$ becomes king and wins $$$Y$$$ but not $$$Z$$$. As such, the final arrangement is $$$YXZ$$$. The claim here is that $$$X$$$ and $$$Z$$$ cannot become RED.
For $$$X$$$, $$$X$$$ beats $$$Y$$$, We have $$$B_X > A_Y$$$, but since $$$A_X > B_X$$$ and $$$A_Y > B_Y$$$, we get that $$$B_Y < A_X$$$. As such, $$$X$$$ cannot be RED.
For $$$Z$$$, we have $$$C_X < A_Z$$$ (since X lost to Z) and $$$B_X < C_X$$$, we hence have $$$B_X < A_Z$$$. As such, $$$Z$$$ cannot be RED
Finally for $$$Y$$$, it is possible that it turns from RED to NONRED.
From these we can conclude that RED cannot be created, but can be destroyed.
REDs can only be destroyed at most $$$O(n)$$$ times.
Simulate a lot "uneventful" moves at once.
Consider NONRED positions to be fixed, and the REDs rotate anti-clockwise about them.
After $$$n-1$$$ moves, what do you observe?
Do many sets of $$$n-1$$$ moves at once until a RED is destroyed or when the game ends.
How to find when a RED is destroyed or when the game ends event occurs quickly?
As such, we have the following conclusions:
- REDS are never created only destroyed
- The order of NONREDS will not change unless a RED inserts itself within the sequence
- REDS will never battle REDS (because of * assumption)
Since the number of times REDS can be destroyed is limited, we should exploit that. We define an event as either when a RED is destroyed or when the game ends. Since events can occur at most $$$O(n)$$$ times, we just need to find some way to quickly simulate the moves until the next event.
Let's visualize the moves like this: instead of the RED and NONRED swapping positions, the NONREDs are fixed in position, and the REDs move around anticlockwise.
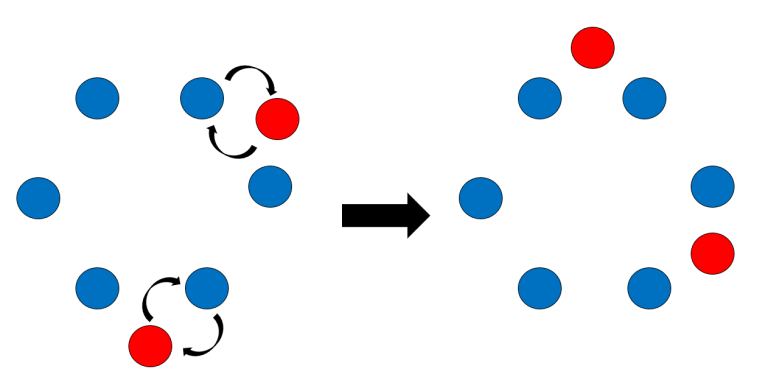
After $$$n-1$$$ moves, every RED moves one space anticlockwise around the belt of NONREDs Then in that case, we just need to check how many sets of $$$n-1$$$ moves is needed until the first event occurs.
For convenience, let's split NONRED into BLUE and GREEN. If a NONRED beats a red in front of it, and it loses to next animal, then it is BLUE. If it wins one more time (and hence the entire game) it is GREEN.
Let's look at the conditions for the events:
- A RED is destroyed. This occurs when $$$B_{nr} < A_{r}$$$ where $$$nr$$$ is any BLUE or GREEN
- The game ends. This occurs when $$$B_{g} > A_{r}$$$ where $$$g$$$ is any GREEN
To find the first how many times the reds need to move anticlockwise, we could maintain a monotonic vector across the belt of NONREDs, and then for each RED, binary search the earliest position where an event occurs.
Finally, when we find the number of sets of $$$n-1$$$ we need to move backwards, we move everything manually, check if the game ends. Then we recompute the color of all animals, and repeat. If no event occurs, then it will repeat infinitely.
The step of finding the number of steps before first event occurs takes $$$O(nlogn)$$$ in total. Since REDs can disappear at most $$$O(n)$$$ times, then the total time complexity is $$$O(n^2logn)$$$.
It's worth noting that the constant factor for this algorithm is small as the number of REDs is $$$0.5n$$$ and binary search is a very fast log. Hence, it passes quite comfortably (author's solution is under 400ms) even though $$$n \leq 6000$$$.
In terms of implementation, we can run the first $$$2n$$$ by brute force just to handle some bad corner cases. In particular, it is mostly to handle the assumption "We can assume no two animals are consecutively RED".
If two animals are consecutively RED, then working out the inequalities will show that the one right before the two REDs should be able to win, and hence the game should end within $$$2n$$$ moves.
#include <bits/stdc++.h>
using namespace std;
const int RED = 0, BLUE = 1, GREEN = 2;
const long long inf = 1e16;
typedef pair<long long, long long> ii;
typedef pair<long long, ii> iii;
long long n;
struct animal{ int a, b, c, id, pos, colour, redHere; };
vector<animal> belt;
vector<animal> arr;
vector<iii> s; ///strictly increasing stack
vector<ii> reds;
void insert(long long b, long long beltPos, long long pos){
while(!s.empty() && s.back().first >= b) s.pop_back();
s.push_back(iii(b,ii(beltPos, pos)));
}
long long totalMoves = 0;
void brute(){
deque<animal> q;
animal w = arr[0];
for(int i = 1;i < n;i++){
q.push_back(arr[i]);
}
long long count = 1;
for(int x = 1;;x++){
if(x > 2*n){
return;
}
if(count == 3){
cout << w.id << " " << x << "\n"; // << "\n" << (int)((clock() - start));
exit(0);
}
if(count == 1){
if(w.b > q.front().a){
animal y = q.front();
q.push_back(y);
q.pop_front();
count++;
}
else{
q.push_back(w);
w = q.front();
q.pop_front();
count = 1;
}
}
else{
if(w.c > q.front().a){
animal y = q.front();
q.push_back(y);
q.pop_front();
count++;
}
else{
q.push_back(w);
w = q.front();
q.pop_front();
count = 1;
}
}
}
}
int main(){
ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin >> n;
for(int i = 0;i < n;i++){
int a, b, c; cin >> a >> b >> c;
assert(a > b and b < c);
arr.push_back({a,b,c,i,-1,1,-1});
}
if(arr[0].a > arr[1].a) swap(arr[0],arr[1]); ///settle first game
arr.push_back(arr[0]); arr.erase(arr.begin());
brute();
///deciding which are RED
for(int i = 1;i < n;i++){
if(arr[i-1].b > arr[i].a){
arr[i].colour = RED;
}
}
///for non-RED, decide if it's BLUE or GREEN
for(int i = 0;i < n;i++){
arr[i].pos = i;
if(arr[i].colour == RED) continue;
int nxt = i+1; if(nxt == n) nxt = 0;
if(arr[nxt].colour == RED) nxt++; if(nxt == n) nxt = 0;
if(arr[i].c > arr[nxt].a) arr[i].colour = GREEN;
else arr[i].colour = BLUE;
}
///get ready the belt
arr.push_back(arr[0]);
for(int i = 0;i < n;i++){
if(arr[i].colour != RED){
if(arr[i+1].colour == RED){
arr[i].redHere = arr[i+1].pos;
}
belt.push_back(arr[i]);
}
}
while(true){
s.clear(); reds.clear();
///Account for cyclic nature, so every element is inserted once, then later inserted again
for(int i = 0;i < (int) belt.size();i++){
animal A = belt[i];
if(A.colour == BLUE) insert(A.b, A.pos, i);
else insert(-inf, A.pos, i); ///GREEN trigger events regardless of the value of a
}
long long minMoves = inf;
for(int i = 0;i < (int) belt.size();i++){
animal A = belt[i];
if(A.colour == BLUE) insert(A.b, A.pos, i);
else insert(-inf, A.pos, i); ///GREEN trigger events regardless of the value of a
///find the RED at that position, if any
int red = A.redHere; if(red == -1) continue;
reds.push_back(ii(red, i));
///find the earliest event that triggers this RED (rightmost non-Red with nonRED.a < RED.b or rightmost GREEN)
auto early = lower_bound(s.begin(), s.end(), iii(arr[red].a, ii(-1,-1)));
if(early == s.begin()) continue; ///no event in this case
early--;
///Number of rotations before event (rotation = N-1 turns)
long long distance = i - (early->second).second;
if(distance < 0) distance += (belt.size());
minMoves = min(distance, minMoves); ///find the minimum number of rotations
}
///No event can occur, answer last infiinite
if(minMoves == inf){
cout << "-1 -1";
return 0;
}
else if(minMoves != 0){ ///Move the reds CCW along the belt
totalMoves += minMoves * (n-1);
for(ii R : reds) belt[R.second].redHere = -1;
for(ii R : reds){
int pos = R.second;
pos -= minMoves; if(pos < 0) pos += belt.size();
belt[pos].redHere = R.first;
}
}
ii ans = ii(inf, inf);
///Updating the belt
for(int i = 0;i < (int) belt.size();i++){
if(belt[i].redHere == -1) continue;
animal R = arr[belt[i].redHere];
if(belt[i].b < R.a){ ///BLUE type event occured
belt[i].redHere = -1;
belt.insert(belt.begin()+(i+1), R); ///inserting in middle of vector
///updating the colours of the surrounding non-REDs
if(belt[i].c > R.a) belt[i].colour = GREEN;
else belt[i].colour = BLUE;
int nxt = i+2; if(nxt == (int) belt.size()) nxt = 0;
if(belt[i+1].c > belt[nxt].a) belt[i+1].colour = GREEN;
else belt[i+1].colour = BLUE;
}
else if(belt[i].colour == GREEN){ ///GREEN type event occured, game ends
ans = min(ans, ii(totalMoves + R.pos + 2, belt[i].id));
}
}
if(ans.first != inf){
cout << ans.second << " " << ans.first;
return 0;
}
}
}
//雪花飄飄北風嘯嘯
//天地一片蒼茫
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/rope>
using namespace std;
using namespace __gnu_pbds;
using namespace __gnu_cxx;
#define ll long long
#define ii pair<ll,ll>
#define iii pair<ii,ll>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << " is " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define up upper_bound
#define rep(x,start,end) for(auto x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
#define indexed_set tree<ll,null_type,less<ll>,rb_tree_tag,tree_order_statistics_node_update>
//change less to less_equal for non distinct pbds, but erase will bug
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
struct dat{
int a,b,c;
int idx;
};
int n;
dat head;
deque<dat> dq;
dat state[6005];
dat trans_belt[6005];
bool green[6005];
int curr;
ll moves=1;
void brute(){
rep(x,0,1000000){
if ((curr==0?head.a:(curr==1?head.b:head.c))>dq.front().a){
dq.pub(dq.front());
dq.pof();
curr++;
if (curr==3){
cout<<head.idx<<" "<<moves<<endl;
exit(0);
}
}
else{
dq.pub(head);
head=dq.front();
dq.pof();
curr=1;
}
moves++;
if (x>n && curr==1) break;
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n;
rep(x,0,n){
int a,b,c;
cin>>a>>b>>c;
if (!x) head={a,b,c,x};
else dq.pub({a,b,c,x});
}
curr=0;
brute();
//convert to state
state[0]=head;
rep(x,1,n) state[x]=dq[x-1];
while (true){
//cout<<"move: "<<moves-1<<endl;
//rep(x,0,n) cout<<state[x].idx<<" "; cout<<endl;
vector<ii> stk;
//find the first instance where state[z].b<state[x].a
//maintain min stack of state[z].b
//now, we focus on the belt itself
//there is a case where the red does not convert to a anything but the game ends
//we need to handle that case carefully!
//i think lets just insert it into stack with value -1
//then if it appears its easily handled
memset(green,false,sizeof(green));
int cnt=0;
int pidx=-1;
rep(x,0,n){
if (x && state[x-1].b>state[x].a){ //red
}
else{ //not red
if (pidx!=-1 && state[pidx].c>state[x].a){
green[pidx]=true;
}
pidx=x;
}
}
if (state[pidx].c>state[0].a) green[0]=true;
rep(x,0,n){
if (x && state[x-1].b>state[x].a){ //red
}
else{ //not red
int temp=green[x]?-1:state[x].b;
while (!stk.empty() && stk.back().fi>temp) stk.pob();
stk.pub(ii(temp,cnt));
cnt++;
}
}
int best=1e9; //shortest distance until red becomes not red
int cnt2=cnt;
//cout<<"non-reds: "<<cnt<<endl;
rep(x,0,n){
if (x && state[x-1].b>state[x].a){ //red
if (stk.front().fi>state[x].a) continue; //it wont become red here
int lo=0,hi=sz(stk),mi;
while (hi-lo>1){
mi=hi+lo>>1;
if (stk[mi].fi<state[x].a) lo=mi;
else hi=mi;
}
//cout<<"debug: "<<x<<endl;
//for (auto &it:stk) cout<<it.fi<<"_"<<it.se<<" "; cout<<endl;
//cout<<state[x].a<<endl;
//cout<<"found: "<<pos[stk[hi]]<<endl;
int dist=cnt2-stk[lo].se;
//cout<<dist<<endl;
if (dist<best){
best=dist;
}
//cout<<endl;
}
else{ //not red
int temp=green[x]?-1:state[x].b;
while (!stk.empty() && stk.back().fi>temp) stk.pob();
stk.pub(ii(temp,cnt2));
cnt2++;
}
}
//cout<<"number in belt: "<<cnt<<endl;
//cout<<"d: "<<best<<" "<<idx<<endl;
if (best==1e9){
cout<<"-1 -1"<<endl;
return 0;
}
//we simulate best-1 cycles for the reds
best--;
//cout<<"hmm: "<<endl;
//cout<<best<<" "<<cnt<<endl;
if (best>=0){
moves+=best*(n-1);
//cout<<endl;
cnt2=0;
rep(x,0,n){
if (x && state[x-1].b>state[x].a){ //red
}
else{ //not red
trans_belt[cnt2]=state[x];
cnt2++;
}
}
//rep(x,0,cnt2) cout<<trans_belt[x].idx<<" "; cout<<endl;
rep(x,n,0){
if (x && state[x-1].b>state[x].a){ //red
}
else{ //not red
cnt2--;
//cout<<x<<" "<<(cnt2-best+cnt)%cnt<<endl;
state[x]=trans_belt[(cnt2-best+cnt)%cnt];
}
}
}
//cout<<cnt<<endl;
//cout<<"move: "<<moves-1<<endl;
//rep(x,0,n) cout<<state[x].idx<<" "; cout<<endl;
head=state[0];
dq.clear();
rep(x,1,n) dq.pub(state[x]);
curr=1;
brute();
//convert to state
state[0]=head;
rep(x,1,n) state[x]=dq[x-1];
//cout<<"move: "<<moves-1<<endl;
//rep(x,0,n) cout<<state[x].idx<<" "; cout<<endl;
//cout<<endl;
//break;
}
}











oolimry orz
oolimry orz
What is orz?
seems it:
We can alternatively use OTL
i prefer nO
OTL????
oolimry orz
Is there any stream coming up for post-contest discussions?
No one as per I notice for this contest.
In the editorial for D, it has the & thing
yep it was fixed. writing
&on codeforces latex equations is finnicky :/ you have to do\\&There is still the & thing in the solution part for D
I thought D very differently
Observations :-
If you want to reach from X to Y
1) X>Y this case is a clear NO. it needs no explanation.
2) THE NUMBER OF SET BITS IN Y can never be greater than X if you want to reach from X to Y.
3) IF YOU HAVE AN ODD X then you can reach every Y which has number of set bits less than of equal to Number of set bits in X.
4) NOW IF YOU HAVE AN EVEN X , I was stuck on this case and had no patterns to observe , if anyone has done it this way , please share your approach
I think your case 3 is wrong. Consider X=
1000110and Y=0111001where least significant bit is on the left. We cannot obtain Y from X.I think the case you have given me has number of Set Bits in Y as 4 and number of set bits in X is 3 , My case 3 says for Odd X we can reach any Y which has number of set bits less than or equal number of set bits in X.
wait sorry. X=
10011100and Y=01100001Another thing you have to check is that there exists a matching. Here, the $$$2$$$ bits in Y can only use $$$1$$$ bit in X.
ok lemme see this case once
I have got accepted in this way. Idea was if you want to reach X to Y then Y have to be smaller or equal than X, number of setbits in Y should be less or equal than number of setbits in X and all setbits index in Y should be later or in same index corresponding to X. Because if one of the setbit of Y is before the corresponding setbit of X then you will never decrease Y to X.
As a Chinese writer, here is the Chinese version of the tutorial (A-H).
Hope you enjoy it. :D
UPD: The tutorial of problem I has been attached.
Can Chinese visit internet? I heard that China is the censorship king? Are you here through a VPN?
You spelled north korea wrong
A perfect round I see.
And I want to explain why some people fst on H.
They pushdowned lazytag to every a in the block.
It's wrong actually. Its complex is $$$O(n^{\frac{5}{3}})$$$
I am sorry to say that I thought it when I doing with my data, but I think no one would write like that because it's easy to change it into just pushdown when query.
Sorry for the fster.
FST is the soul of CF. —— Sooke
[user:Wodiwmaker] What is "fst" ?
Edit: Ans->FST is short for failed in system testing.
In the problem B there are some cases when |a[i] — a[i — 1]| > 1, but answer is not 0.
One of that cases is:
n = 4 a[1] = 1 a[2] = 3 a[3] = 1000001 a[4] = 1000000
If we want to reach to the node (4, 1000001), we will move one of the obstacles in node (3, 1000001) or (4, 1000000).
This means, that in this case answer is not equal to 0.
1 <= a[i] <= 10^6
I'm sorry, but I'm honestly not sure how it's even possible to write such egregiously weak pretests. My E fails on any test case where N is not a Fibonacci number, as it doesn't return after printing no (and thus prints either yes or a second no afterwards), and yet it passes all pretests and ultimately gets FST24. I would understand the FST if I had some minor bug in an edge case, but a generator that outputs trees completely at random would fail my submission nearly 99.99% of the time. (And evidently, pretests for A, B, C, and G weren't so strong, either...)
I would have assumed y'all were intentionally aiming for weak pretests if not for the comment on the other thread hoping for few FSTs. Especially given that comment, I think it was pretty reasonable to assume that a test covering this sort of case was included in pretests. I appreciate the preparation that went into the remaining problems, but it probably shouldn't be too hard to understand why losing 90 rating over this FST sours my opinion of this round in general.
LOL the same thing happened to me too. I got RE on test 24 (my code also fails in any test where n is not a fibonacci number). That's very upsetting because I could have found my bug in a few minutes and the effect of this minor error cost me over a 100 rating points (and a t-shirt :( )
I want to say a lot, but I can just say sorry now.
I did write a generator for that case.
It has 1/5 posibility to generate a non-fibonacci-number $$$n$$$.
For some reason, I just upload it and add a test to tell them I have written a generator for E.
But they write a new generator and forget this case.
So finally We just used that to create a test however. And unluckily, it's not in that case.
Sorry again :sadness:
I saw tourists solution of C in O(n) using DSU, how to solve it using DSU?
Typo in the solution for 1491D?
bit from v from u from theCan we get an example for this — 1491D
We can convert any u+v move to a series of u+v′ moves where u&v′=v′ and v′=2k.You serious?
5000 score bro.
Got the correct idea of E but failed to implement it :(
same
same, just missing a "break" :(
Problem B got me confused with the constraints during contest. Didn't realise that the obstacle can't be placed on first and last column which led to completely different approach. And rather complex bounds to deal with.
I realized this only after reading your comment. OMG.
I think I have the same logic in 2nd question but the test didn't pass. How can I know which test case made it wrong?
You can scroll down through your submission to see on which case your o/p differ. But there is limitation to number of test case shown.
Peko Peko
I think C's editorial is kinda overcomplicated although the final idea is the same. You always need to start from the first s_i that is not 1 and perform s_i-1 jumps, then it is just a simulation problem.
Can u demonstrate plz more ? I did the following : each number can't be more than 5000 (worst case) because it throws the rabbit out so we add to the answer A_i — 5000 if A-i >5000 then iterate from left for every value that is not 1 run a simple DFS starting from this index until it becomes 1 and simulate the process but that was TLE since it is O(n³) I need to improve it to become O(n²)... thanks in advance.
Just maintain an array nxt[i] for the position of next non-1 number after i. Then if a[i] is 1, use nxt[i] instead of simply i++.
Since after use nxt[i], you can always land on a non-1 number and decrease it by one. And the initial total height of all a[i], as you said, is at most 5000*5000. Therefore, this solution is O(n^2).
Can you please explain the solution to C a bit in detail , I can't get what the editorial is trying to say at all
thanks, upsolving time
what about when the obstacles in (0 ,1) and (n-1 , 1e6+1) in problem "B"!!
The first and the last column are excluded from having obstacles, see the constraints!
It is written that 1<=a[i]<=1e6
In problem E, I started dfs from 1 and calculated the sizes of all the subtrees and checked whether the size of any subtree is a part of fibonacci sequence, but can anyone please explain why it gave wrong answer on pretest 14, link to my SOLUTION. Thank you :)
I got WA using the same algorithm, and find the counter example:
Can anyone explain C better that is what is happening in editorialists solution?
Have an array curr which holds all the jumps made on an index.
For an index i:
if the jumps made so far (curr[i]) were not enough to get it to 1, then add to the solution the remaining Si-1-curr[i] jumps (each of these jumps is a new pass because i is the first non-1 trampoline).
after the if is executed, temp is the number of jumps on index i
temp — (Si — 1) = the number of jumps on index i — the number of jumps necessary to get to strength 1 = all the jumps that jumped to i + 1. So we add all of these jumps to curr[i + 1]
add 1 jump to curr[j] for j in range [i + 2, i + Si]. These jumps are performed in order to get the trampoline i to strength 1
emp — (Si — 1) = the number of jumps on index i — the number of jumps necessary to get to strength 1 = all the jumps that jumped to i + 1. So we add all of these jumps to curr[i + 1]
can you explain this part a bit ! I just cannot understand how is this true ?
When the for loop gets to index i:
curr[i] represents the number of jumps that happened already on trampoline i
curr[j] where i < j (all indexes to the right of i) represent the number of jumps on trampoline j that were the second jump of a pass. This is the key point. If a pass started at index 1, jumped from 1 to 3 and from 3 to j, this jump on j is not yet added to curr[j].
Example: Si = 3, curr[i] = 5.
The first jump gets us to i + 3 (we add this to curr[i + 3])
The second jump gets us to i + 2 (we add this to curr[i + 2])
Jumps 3,4,5 jump to i + 1 but we don't add +3 to curr[i + 1] in the second for loop, that only does cur[j]++. So when we get to index i, we add these 3 jumps to i + 1. This is done in curr[x+1]+=temp-arr[x]+1;
can someone explain c more clearly?
someone please Explain C ..... the editorial is too complex at least for me
Same here
You have to jump on the first number which is greater than 1, then just add 1 to all the further indexes where current number will jump (for this you can keep an temp array) and for any further number check how many times you came on it already , then jump more if then number is still greater than 1
it's clear that for each i from 1 to n you have to jump in the i'th position a[i]-1 time right?
ok we will do it lets start from the first position and jump on it until it become 1 but on each jump on this element tell the next positions that you have jump to them
how??
ok if n = 10
and a[1] = 5
in the first jump you will go to the position 1+5 ok just tell the 6'th position that you will go to him
know a[1] = 4 and that next jump will take you at the first step to 1+4 yes tell the 5'th position you will go to him
when a[1] become 1 you will have told each position that you will jump to him
so when you go to i+1, i+2, i+3.... you can know that you jump on the current position some times if this number of jumps grater then a[i]-1 you don't have to make any other jumps in the current position else you will do the remain jumps
but don't forget you have just calculate one step from each position to another so when you are in some position j you have to till the next positions that you are jumped on them
O(n^2)
now i know the basic O(N^3) solution with help of some and your comments. can you explain how to reduce it to O(N^2) time complexity?
So basically what I can conceive is that we don't really wanna do the jumps as in a simulation but all we do is store where those jumps are going to be so that when we want to start the procedure at index j we will determine if that index is already has become 1 or it is valid to start another jumping journey from it . If I'm right then your explanation should really be the editorial :D
I finally get how to solve C. Here's how:
Problem Recap
Jump from any trampoline (say index 'i'), land at index (S[i] + i). If index (S[i] + i) is in bounds, then continue jumping in a similar manner until you're out of bounds. At each hop, you're reducing the trampoline's strength by 1. Make all trampolines' strength 1. How many initial jumps does it take?
Observations
Reference
Thanks for the clean explanation!
Thanks a lot. Nice explanation!
This is best to be included in official editorial.
Thanks for the explanation. But I am not getting what pref[] array is storing. I got that starting from any non-zero value of s[i] we can increment the range (i+s[i],i+2) by 1 and when we will get there we will decrement that s[j] by 1+pref[j] but how we are maintaining this pref[] array?
In general, pref[i] stores t[i]-t[i-1], where t[i] is the number of ranges that started at some j<=i and will end at some k>i. Notice that we can always derive t[i] from the pref array, using the formula t[i] = pref[0] + ... + pref[i]. If i is running from 0 to n-1, deriving t[i] per i is O(1), since pref[0]+...+pref[i-1] is pre-computed. The advantage of maintaining pref[] (instead of t[]) is that, updating information for a range is faster: just 2 operations (Observation 3 in sh_maestro's post). Whereas if we maintained t[], that would be linear in the size of the range.
Thanks for replying.
Thanks for the descriptive explanation.
Thanks, very nice explanation, I just to understand point $$$6$$$
what is incoming hops, did you mean $$$pref$$$
can you please elaborate more on point $$$6$$$.
I have implemented this during contest, but it did not work.
I think incoming_hops[i] is the total number number of jumps from previous positions to position i. We have that incoming_hops[i] = pref[0]+...+pref[i] = incoming_hops[i-1] + pref[i]
I'll elaborate here (I've also added a little more context to the original explanation)
pref[] is the same as incoming hops. When you are at index i, you need a way to designate the indexes that index i will hop to. Say the trampoline at index i has a strength of 5 and hence hops from indexes (i + 2) to index (i + 5). pref[] will add 1 for each element between these 2, inclusive (i.e. pref[i + 2]++, pref[i + 3]++, pref[i + 4]++, pref[i + 5]++). Note that you don't actually need to update each index as that would be an expensive O(N) operation. You can do it in O(1) by simply updating the bounds (one at start, and one right after end) and have a rolling prefix sum to calculate the net result so far (pref is called "here" in the reference code — I should've been more consistent).
To elaborate on point 6 (which is now point 7 since I added one), consider this example:
At index 1, a strength of 4 means that it will initiate 3 jumps (to indexes 3 through 5). Lets update pref accordingly.
Move to the next trampoline to its right.
At index 2, initiate 3 more jumps (to indexes 4 and 5 and once out of bounds).
Done with this trampoline. Move on to index 3.
At index 3, notice that there was 1 prior jump so 2 (i.e. pref[3] == 1) new jumps need to be initiated to bring its strength to 1. Total of 3 jumps (one prior, 2 new) — once to index 5 and twice out of bounds.
Done. Lets move to index 4.
Now, index 4 is different from the rest. It has had 2 incoming jumps and has a strength of 2. The first hop makes it jump out of bounds, and brings its strength down to 1. The second hop makes it jump to index 5 (i + 1, instead of the i + 2 that we've seen so far). Had there been a third jump, that would've gone to index 5 as well. Note that the answer remains 8 since no new jumps had to be initiated here.
Finally we move to the last index
Here again, the incoming jumps (pref[5] = 4) exceed strength — 1 (3 — 1 = 2) by 2. So no new jumps need to be initiated and the answer remains 8.
Excellent explanation, this is more than what I could hope for! thank you so much for your time.
Just want to say thank you! Finally understood the solution.
Why we can't start from 1 as we eventually reach first non-one and it did not increase the pass count ?
Good point. You could start from the first trampoline on the left — it has the same effect as starting from the first trampoline with a strength greater than 1. I've updated the text around this.
I have 2 questions: 1.) What is "count" doing? 2.) Why decrement one from the position after range? I mean, why here[mx + 1]-- and why not here[mx]--?
1) after some pass s[i] will be equal to 1. then pekora will jump from i to i+1 trampoline when it is on i-th trampoline . here count variable counts the number of incoming hops on i after s[i]=1
2) to increment the number of incoming hops from i+2 to i+s[i]. To understand it better you can read this article.
To your first question:
"count" tracks the number of extra hops (i.e. for any index i, it's incoming hops — (strength — 1)). The reason for counting this separately is that these hops will all go to index i + 1.
To recap, if incoming_hops is 10, and strength is 4. Then the first 3 hops will go to indexes i + 4, i + 3 and i + 2. At that point the strength becomes 1. But there are still 7 (10 — 3) more incoming hops. Those 7 will all go to index i + 1.
To your second question:
When you want to add an "amount" to a range [l, r] (both inclusive), the way you do it is to mark pref[l] += amount and pref[r + 1] -= amount. This is because you want pref[l] through pref[r] to all get incremented by that amount, and then decrement by the same as soon as you step beyond r. Then at each index, you accumulate the sum. So pref[l + 1] += pref[l], then in the next iteration pref[l + 2] += pref[l + 1], etc. — this way the sum gets carried over from the current index to the next.
The link shared by Saimun_Islam explains it in detail.
This is optimal as we can consider the first trampoline that Pekora jumps on for both these passes. It is clear that the series of trampolines jumped on in these 2 jumps does not change.
Please someone explain this in Problem C.
It basically says that you can freely exchange the order of trampolines you choose to start and the resulting strengths in the end will always be the same. You can play around with some examples to see why this is true.
Can anyone help me to figure out why and where I am getting that one extra (0/1) in the answer in Testcase 2 in Problem A Solution . Thanks in advance for your help.
There are q queries not n queries. See the input section.
My self worth took a big hit during this contest.. The round was really great though! Kudos to the authors..
The problems had a lot of variety. I appreciate your hard work in setting such a nice contest and for such a quick editorial. Wish more such contests keep happening!
Your solution is O(n^3) !!
I've done C with a lazy propagation segment tree (adding a constant on the range), so my solution is O(n log n). Any ideas how to get to O(n)?
You need to add on range right, so you can just maintain a array and increase $$$l$$$ by $$$1$$$ and decrease $$$r$$$ by $$$1$$$. So you are just iterating from left and these range additions are also accounted for.
ahh yes, that trick.. Thank u very much
Can u plz explain your approach ? I'm learning segment tree right now so this would be so helpful
U can learn seg tree here https://cp-algorithms.com/data_structures/segment_tree.html My approach was to have a segtree of lenth n, initially set to zero. Then I would traverse the array from left to right and add the value from index i on the appropriate segment
Please Help meIn Problem C, I have done normal simulation as given in editorialO(N^2)and still am getting TLE on TC 9.My Submission Link https://codeforces.com/contest/1491/submission/108727431
Please Codeforces community
TLE because O(N^3)
The editorial doesn't simulate all the jumps in order. I did, but I skipped all the jumps equal to 1 by using a set of intervals for these trampolines. The code is long and ugly though.
In python solution of 1491C — Pekora and Trampoline
What is the meaning of line
temp+=arr[x]-1-temp
doesn't it just means temp = arr[x] — 1?
no , it means temp = temp + arr[x] — 1
temp += arr[x] — 1 — temp
this is equal to : temp = temp + (arr[x] — 1 — temp)
which means temp = arr[x] — 1
Am I doing anything wrong here?
In problem E, my code will have some problems when n is not a fib number, I noticed that after I locked problem. There is a person in my room who make mistakes with data like this, I submitted a hack data (this data also can hack myself), and it returned unexpected verdict.
I Failed System Test in E, and my hack has been ignored. But this submission was hacked by me, I didn't get 100 score.
Why is it?
this is strange!!
雪花飄飄北風嘯嘯 天地一片蒼茫
:D
In fact, I have some questions about the problem B.
In the tutorial, we can find that the answer will be one of the three numbers: 0, min(u, v) and v + min(u, v). But considering the following data:
4 3 4
1 0 1000001 1000000
, we can find that we have to move two obstacles to make sure that we can reach (4, 10000001) from (1, 0). And in my opinion, the answer will be 2 * min(u, v).
If I'm wrong, I'll highly appreciate if you can tell me which condition I missed. Thanks.
Read the problem description carefully.
Oh, thanks. I find that where I'm wrong. The $$$a_i$$$ is not greater than $$$10^6$$$, so the situation I considered won't happen.
Thanks again.
My ugly
O(n^2\log n)solution for C passed...... My solution is simulate the jump, and use a balanced BST to find the next trampoline withS > 1inO(\log n)time. Number of total jumps isO(n^2)My submission for C got TLE even though i'm sure it's $$$O(N^2)$$$, can anyone help me? Probably a problem in the
whileloop but hard to tell for me. Submission LinkNaive simulation is actually $$$O(N^3)$$$. It hits that bound on test
5000 4999 4998 ... 2 1.I probably should make editorial more clear about how to simulate in $$$O(N^2)$$$.
Can anyone explain D to me
means what is the intuition behind this?
Let's take a binary string here as example, 1001100101. Notice that if we pick any number which has one set bit(i.e a power of two) whose set bit lines up with a set bit in the given binary string(for example binary string 100), then its bitwise and will be the string itself(1001100101 & 100 =100). Now when we add the two numbers, two cases might occur. If there are no consecutive set bits ahead of the set bit, then the set value shifts by one bit(1001100101+100=1001101001). If there are consecutive set bits ahead of the set bit, then the first set bit in the consecutive set bits shifts by 1 bit, and the other consecutive set bits disappear(1001100101+100000=1010000101). So if we can reach number v from number u by applying these two possible operations, then there is a path between them.
Can someone tell me what is wrong in my submission for problem E? I am getting WA on Test 14
1491E - Fib-tree — 108766255
Can anyone help me out why am i getting WA on test case 8 in E My submission — Your text to link here...
The problems had a lot of variety. I appreciate your hard work in setting such a nice contest and for such a quick editorial. Wish more such contests keep happening!
Can you explain D bit more ? Why exactly do we want v = 2^k ? And what does this line mean ?
the Python solution in this editorial for problem 1st gets TLE in both Python3 and PyPy 3. So heres my solution which got accepted 108784095
108805120 it doesnt tle?
No, i am talking about 1419A, Kth largest element problem , the solution given in the editorial Your solution is this [submission:108783813]it gets tle
alright ill add your solution into editorial :)
You are super nice. errorgorn orz
Why this number is so common among testers and random generators :XD
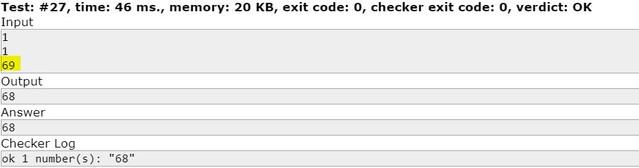
This is the 27th testcase of problem C
You go here.
In the question B, do we have to move the obstacles before starting our movement or can we move the obstacles while we are at some other node(instead of 1,0)? Because then the answer changes for this test case:- 2 100 1 1 2 If we move the obstacle 1 and move it to our current node then we cannot go pass through the obstacle and hence the answer is 2(by moving the second obstacle twice towards right) but if we can move the obstacles during the journey then the answer would be 1. According to the solution the answer should be 1 but according to the problem statement its not possible because then the obstacle is at the starting node.
Nvm I got it. We can move the second obstacle towards the right.
I have a doubt in B. What if the obstacle in last row is present on 10e6+1 and on all rows before that, its present on 10e6 then v is not a possible answer. Please enlighten me.
1<=ai<=1e6. So the obstacle will be never on the column 10e6 + 1.
Thanks I had missed that
Same bro i also missed the part that 1st and last columns are empty. You should try when there are no such restrictions. I submitted a general code assuming no restrictions in the placement of obstacles in column.
Your code doesn't even solve the general case and you have a couple of redundant if statements.
Tell me the test case. I will think about it.
errorgorn oolimry In C editorial's python code is giving tle.
108805120 it doesnt tle?
It gives tle verdict in python3 but not in pypy.
yea pypy3 is super fast compared to python3. you should select pypy2/3 when using python
Can you please tell the DP approach for problem C....I got stuck at it just because I kept thinking that it had to be done using DP
Can someone explain C to me?
Because of greedy works, we should reduce S (to 1) from left to right.
Use tmp(i) to present the numbers of jumping on the i-th Trampoline from Trampoline 1~i-1.
When we come to think about the i-th Trampoline, the first thing we need to do is to add ans with
max(0,S(i)-tmp(i)-1), because we can jump tmp(i) times for free.The next thing we should do is state transition, we should add the tmp(i+2,……,i+S(i)) with 1. tmp(i+1) should be specially handled---add it with
max(0ll,tmp[i]-(S[i]-1))The more detailful things are in my code
A nice contest.
Although it's the first global round I participte in, I perform as good as I expected before the contest.
The first four problems are a little harder than the first fours in the Div.2, and I had a difficult time trying to solve D. (I AC D before the contest ended by 5 mins)
This shows me I still have a long way to go, so I will continue to work hard and improve myself.
Hope everyone can enjoy the contest!
[problem:B] In the statement n is "<= 100", but I can't pass. After I set N as 1e7, I get AC. And in the Tutorial, N is 1e6. So I think the data is different with the statement.
Problem F : As all the previous answers are 0, it's easy to prove that the magnet we found is the second one we have selected.
Is there anyone who can proof it for me?
In problem D, I was not able to prove that if v has smaller or equal no of set bits than u where v>u then we can always reach to v. Can somebody help me in that?
What you are saying is necessary but not sufficient.
For example take (in binary) u = 001001001 and v = 010000011 , clearly v>u and number of bits in v is equal to number of bits in u , but you cannot reach v from u.
We can reach v only if number of bits occurred till position $$$i$$$ in v is less than or equal to number of bits occurred till position $$$i$$$ in u and v>=u (sufficient condition).
One of the way we can approach the proof is that we can shift the bits of u any distance toward left but above condition must hold because whenever we add the subset it increases the u and shifts it's bits toward left by one and may cause some of bits disappear because of adding (they become carry).
00001100011 + 00000000011 = 00001100110 . Here we can see first two bits shifted toward left by distance 1.
00001100011 + 00000000001 = 00001100100 , here we can see that second bit shifted toward 3rd position and first bit disappeared .
Thanks, it's a saviour
Pekora and Trampoline — O(n) Solution
Hi there,
Could I get some help with TLE for E?
108832717
It should have the same complexity as what the editorial says. Is it because I use recursion for my findSplit function?
Thanks!
.
Is there any proof for problem E that Fib-tree can be partitioned within at most 2 ways.
You can notice that parts of size $$$F_{n - 2}$$$ must be disjoint (otherwise it would imply $$$2F_{n-2} \geq F_{n}$$$, which is false). Therefore number of partitions is bounded by $$$\lfloor{\dfrac{F_{n}}{F_{n-2}}\rfloor}$$$.
I added some pictures to explain the proof of E. For a Fib-tree, there are two cases. In one case(see picture below, that's the case described in editorial), there are two ways to cut the tree, both ways are valid.
In another case(see picture below), there is exactly one way to cut the tree: cut "First Edge" first, then cut "Second Edge". In this case, "check $$$F_{n-1}$$$ or $$$F_{n-2}$$$" also works: if tree root is in left two parts, we will find a subtree consists of $$$F_{n-2}$$$ vertices; if tree root is in the right part, we will find a subtree consists of $$$F_{n-1}$$$ vertices.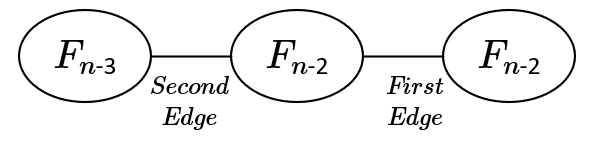
"exchange argument" .How it is used in C? please anyone explain the proof. I can't understand.
Exchange argument is a greedy proof technique that is to show that we can turn any optimal solution into one that our greedy algorithm will produce and it will do no worse. Here we want to show that it is optimal that for each pass, the trampoline that Pekora will start at is non-decreasing.
In the editorial, we have shown that swapping the sequence of any $$$2$$$ consecutive passes does not change the final outcome of the strengths of the trampolines. Therefore, by performing a series of swap, we can sort $$$P$$$ (or you can think of it as bubble sort) for any arbitrary optimal solution $$$P$$$.
For a concrete example, suppose an optimal solution is $$$P=\{3,1,4,1,5\}$$$. Using our proof, we can say that $$$\{3,1,1,4,5\}$$$,$$$\{1,3,1,4,5\}$$$,$$$\{1,1,3,4,5\}$$$ are all optimal solutions.
With respect to problem C: Pekora and Trampoline, I implemented the $$$O(N^2)$$$ solution. However, I still got TLE. In my opinion, an $$$O(N^2)$$$ algorithm would amount to elementary operations of the order of $$$10^8$$$, which should be executed in under $$$2$$$ seconds. I have attached my code below.
My code
If my code is inefficient, please do recommend suggestions. Also, I am aware of the $$$O(N)$$$ solution but I would like to first implement the $$$O(N^2)$$$ solution as it was explained in the editorial that such a solution should also pass the test cases.
Also, please do think before downvoting, and if you still decide to do so consider also informing me what was lacking or offensive in my comment. I have been given a contribution of $$$-1$$$ due to a post of mine but I'm still not able to figure out what was wrong. Due to my negative contribution, I have to face a lot of embarrassment. I hope you understand.
Why set your array size to $$$3000$$$ when $$$n$$$ can be up to $$$5000$$$?
After changing this it got AC.
I don't understand in problem D, why do we have to start checking from LSB instead of MSB ?
You can do both, implementation wise checking and matching from LSB is easier. Check out these submissions : LSB's : 109403908
MSB's : 109404715
Thanks unusual_wonder !
1491G — Switch and Flip
Code (C++)
//雪花飄飄北風嘯嘯
//天地一片蒼茫
(a Chinese song named "A Spray of Plum Blossoms")
I wonder how to construct test cases that need $$$O(n^3)$$$ moves to solve, in Ruler Of The Zoo.
BTW, here are two hacks.
This hacks rainboy :
and this hacks huzhaoyang:
I guess if if after $$$n-1$$$ moves all the reds move anticlockwise once, then you can probably do this for $$$O(n)$$$ times before an event occurs. This in total takes $$$O(n^2)$$$ time for an event to occur.
If we have a lot of REDs, we can make only the last one trigger at the last set of $$$n-1$$$ moves, this will take $$$O(n^2)$$$ moves to occur. Then, since we insert a new BLUE into the belt, we can use this new BLUE to trigger the 2nd last RED, which will require a total of $$$O(n^2)$$$ moves again. Doing this for all $$$O(n)$$$ REDs will require $$$O(n^3)$$$ moves.
Thank you for hack
To construct test cases that need $$$o(n^{3})$$$,I think we can make even positions RED, and then make them NONRED from right to left
More specifically,let Ai,Bi and Ci at odd position be large enough
For even positions,$$$A_{i}=10i$$$,$$$B_{i}=A_{i-2}-1$$$,$$$C_{i}=B_{i}+1$$$
(In particular, $B_{1}<A_{n}$)
I'm sorry for posting this late, but I really need help on problem D. I have a solution but it WAs on token 644 My approach is to try to add the powers of 2 in the binary representation of (v — u) to u from left to right If the bit in both u and v — u is 1 then I add that power of 2 to u and then move towards the left to see if a new bit has been set to 1 that wasn't able to be used before If that bit can be used, add the respective power of 2 and keep moving left The second case is if the bit in u is 0 and if the bit in v — u is 1 Then I used a set to store that that index hasn't been used, next time I reach case 1, I'll be able to use that information to see if I need to use a previous bit Here's my submission: https://codeforces.com/contest/1491/submission/154037118
Is my logic wrong or do I just suck at implementation?