Hi again, it is me. I want to preface this blog by saying that I am totally aware that it is not good netiquette to screenshot private messages and publish them publicly. But honestly, I can't care anymore now.
Below is an unorganized rant. Sorry, I'm too pissed to write the things below concisely. And here: I'm pinging him: wuhudsm.
In an ideal world, I could probably just tell him privately to stop doing it. But I already did. So I think I need to write this blog to either stop him from doing this again or just soft-ban him from authoring more rounds by telling everyone about it.
Let me just preface this blog with a fact of coordination -- it is very possible that problems from contest A will be used in contest B even after testers from contest A have seen those problems. So there are indeed (many) testers who could possibly be affected by this. Some examples of this happening (where I was involved):
- Contest problems based on on-site contests were quite common in the past. A recent example I can think of is 1965F - Conference, where the problem was originally used in Yandex Cup 2023, an entire 6 months ago.
- Contest A has finished, but the author still has quite a few problems. In that case, I would encourage them to set another contest. Some examples of this are CodeTON Round 7 (Div. 1 + Div. 2, Rated, Prizes!) being a descendant round of Hello 2024 (yes, Hello 2024 came first, long story) and Codeforces Round 934 (Div. 1) being a descendant of think-cell Round 1. In both cases, there do exist testers of the former contest who had seen problems that we plan to use in the newer contest. In particular, the last problems from Hello 2024 and round 934 were originally also the last problems of the two other respective contests. We will tell testers of those rounds that they are forced to test or are forced to ignore the problems they have seen before when participating (of course most people ignore d1Fs anyway). On a side note, there are also cases where a few testers have seen a problem before it is removed from testing, where they do indeed have a chance at solving them. An example is 1943D2 - Counting Is Fun (Hard Version). Unfortunately, sometimes for the sake of making a new contest, we just have to tell them "too bad".
Anyway, the point here is that in both scenarios, we make it super transparent to all parties involved that the problems they have seen before should be kept secret, and we intend to use them in a future round. For example, in Yandex Cup, they made it super clear to all participants that contest problems should be kept secret after the contest has ended. I am totally fine with authors proposing problems for multiple contests, just ensure that you explicitly tell the coordinator about it and the coordinator knows. I believe we wouldn't say "no" just to spite you.
Now, I will go into one of the main points. Coordinating rounds involves reviewing problem ideas proposed by authors and selecting some of them to compose a round. If I deem that a problem does not reach certain standards, I will not approve it to be used in a Codeforces round (the inverse is not true). It is sometimes the case where an author proposes many low-quality problems, resulting in most of the proposals getting rejected and increased workload for both the author and the coordinator. wuhudsm is one of them. He proposed many problems, but he doesn't seem to have much quality control over his problems. There was a period of about a week where he would send one or two problems every day (and clearly they were mostly getting rejected).
Now, what do you do when your problems get rejected by a coordinator?
- option 1: deal with it
- option 2 (wtf???): propose it to another publically rated round
Most sensible authors will probably choose option 1. I consider proposing it to local contest, which includes OCPC, is about the same as option 1. In fact, I even encouraged wuhudsm to send his problems to OCPC, and told adamant about inviting wuhudsm to problemset for OCPC.
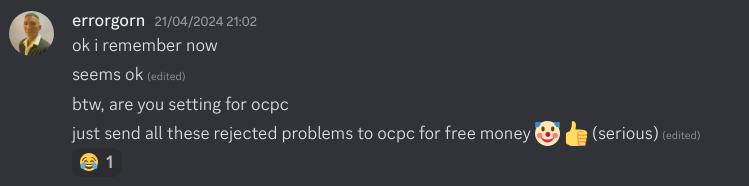

As a sidenote, I just want to make it clear that OCPC is not a place where you send bad problems. It is just that the problem styles of OCPC and codeforces are wildly different. Just like how IOI and CF are both well-respected for having enjoyable problems, but a good problem for CF may not be a very good problem for IOI and vice versa.
I wouldn't pay $1000 to go to Croatia onsite for OCPC Fall 2024 if I thought it was a joke, right?
The other thing about choosing option 2 is that it further reinforces the idea that you are problem-setting for the sake of it and don't really care about the quality of your problems and the contest. You don't care how your problem is in a contest, just that it appears in a contest; you are just hoping that some coordinator has a taste that accommodates your problem. Now, I want to point out here that if you think that your problem was wrongly rejected, you are free to argue with me. In fact, there are cases in the past where I asked another coordinator for a second opinion (with the author's permission, of course) because I understand that one's taste in problems can be very skewed.
Bad proposals are one thing. What truly enrages me is proposing the same problems to other contests without informing me. It was only recently that I learned that half the problems in wuhudsm's OCPC round were actually problems I had seen before. But oh well, whatever, I think my team is definitely strong enough to get a good ranking without me anyway. I don't really mind sitting out. The problems are actually fine, and OCPC is not a scam.
If this were only a one-off thing, I wouldn't bother to write this blog. Here are more examples of wuhudsm not informing coordinators that a problem he had proposed was already proposed to another contest.
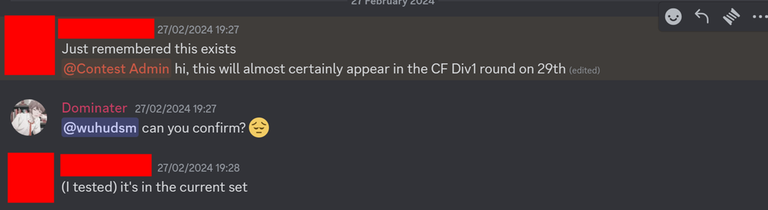
The first sign came back in March 2024, where max-average-path was a problem that was accepted in his proposal that I was coordinating.
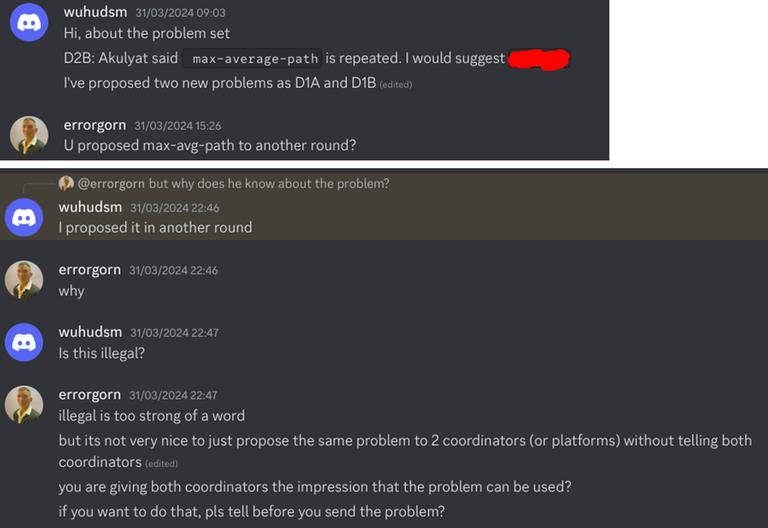
Note that his round with Akulyat was actually the recent round 1990. Now, note that the round I was coordinating and round 1990 only had a single author — wuhudsm. I was under the assumption that the round with Akulyat was proposed as a group of authors, so I did not think too much about it. And since this was the first incident, I just gave him the benefit of the doubt.
Then, after the OCPC incident, I was talking with TheScrasse about coordinating stuff, and wuhudsm's name popped up in the conversation. Then I realized wuhudsm has a round with me, Akulyat and TheScrasse all at the same time, which I presume are all set individually. From here, I had an instinct that wuhudsm probably had proposed a lot of problems I had seen to TheScrasse already. So, I asked TheScrasse if I could merge the rounds coordinated by me and him so that he would coordinate both rounds (the set of authors is exactly the same). It was then that TheScrasse said he had already seen half the problems already. This triggered a stupid amount of red flags for me.
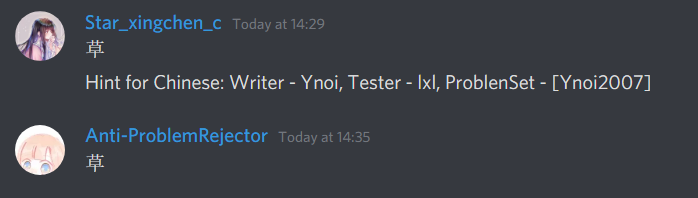
Then, yesterday, Codeforces Round 960 (Div. 2) was released. I realized that I had seen problems E and F before. Here is evidence that I have seen them before:
Note that these 2 problems are still marked as "accepted" in the proposal, indicating that they are potential candidate problems to be used in a contest. If they were rejected problems from my contest, I guess I could still close 1 eye about it.
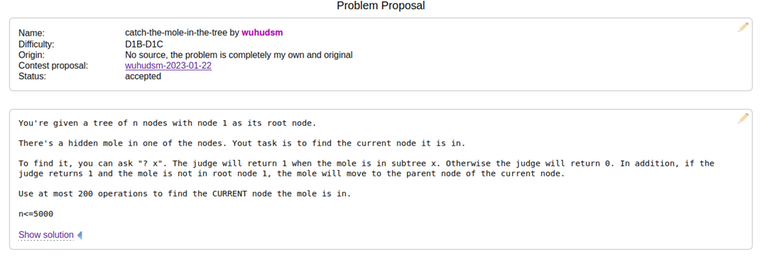


This was written on March 25

This gave a lot of red flags to me. I decided to check with CodeChef about this, and indeed the same thing happened in CodeChef. Thanks to Dominater069 who gave me this evidence.
The only way they got to know that some problem is going to be used is when they tried to use it themselves.
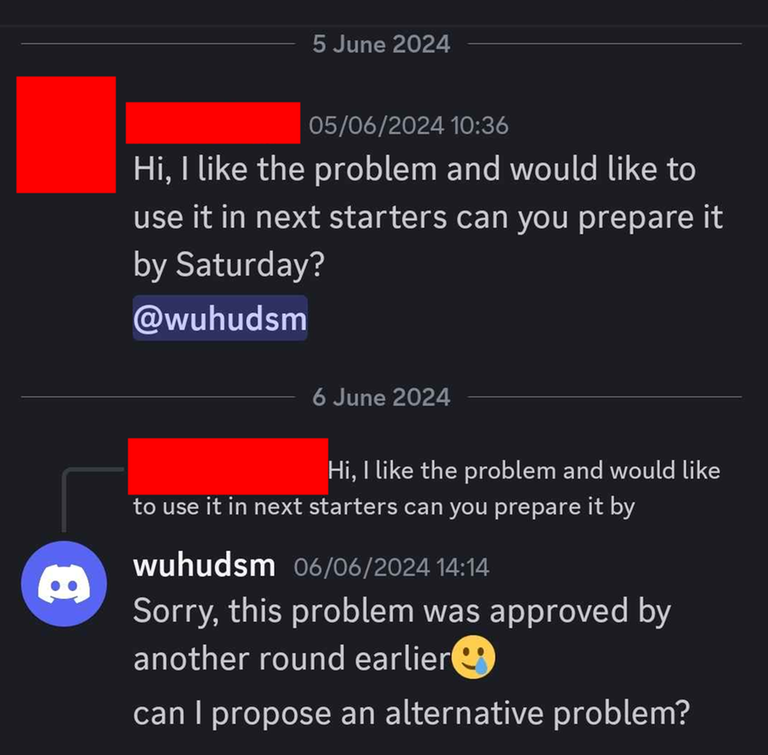
Another problem which CodeChef admin asked if he can use. This ended up being 1936E - Yet Yet Another Permutation Problem.
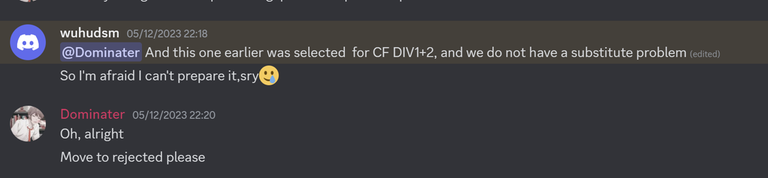
The same 1936E - Yet Yet Another Permutation Problem problem, but wuhudsm did not mention which contest the problem was going to be used, so it was only by chance that a CodeChef admin had tested the round in question and informed them (just a few days before the round).
Anyways, to the point of this blog is that if anyone wants to let wuhudsm be an author, they should be extremely cautious about it. The fact that this has happened so many times says a lot about it.
Well, to end this blog, I am going to announce my intention to quit coordinating, which I had decided quite a few months ago. I will officially retire after completing the coordination of rounds currently assigned to me (currently 5 div 1 rounds and 1 div 2 round). I joined Codeforces as a coordinator around December 2021 because I enjoyed helping talented authors bring their beautiful problems into a contests for people globally to enjoy. The journey has been amazing and I collaborated with many talented authors from all over the world. I still think fondly of the times where I would be talking nonsense with authors in their testing server or in voice channel.
However, I have probably burnt out a long time ago. Coordinating takes too much of a mental toll on me and I have to force myself to coordinate the remaining rounds. It is time for me to move on to other things in life. Furthermore, I don't think it is fair for me to continue coordination as I definitely would be not be able to maintain the standards of coordination I had in the distant past. I might write more personal thoughts in my own blog when I feel like it.
However, this is not a goodbye to Codeforces and competitive programming (I still have yet to participate in ICPC). I just wish to go back to being a humble competitor of competitive programming.
EDIT
I have asked Akulyat about his side of the story, for 1990E2 - Catch the Mole(Hard Version) and 1990F - Polygonal Segments. He has agreed to be quoted in this blog.
When I asked him about whether he knew wuhudsm had proposed problems in his proposal to other contest, he replied.
No, I didn't know about any of them being proposed to other contests. Seeing the amount of proposed problems I assumed that some of them were proposed to other contests but I thought that rather to those that had passed.
According to him, 1990E2 - Catch the Mole(Hard Version) was proposed on 24th of april, and an array version was proposed earlier. Looking at both timelines, this means that wuhudsm proposed this problems to the coordinators at the same date, most likely before anyone of us responded to it.
Then, 1990F - Polygonal Segments was proposed in Feburary. Where I assume Akulyat did not look at it until the proposal was assigned to him later. Akulyat responded to the problem on 2nd of April. For me, the problem was proposed to me on 23rd March. That means, the same thing happened again. wuhudsm proposed the same problem to 2 different coordinators before any of us responded to it.