So my O level Chinese exam is in 2 days so I decided to learn a data structure that I can only find resources for in Chinese. I thought I might as well write a tutorial in English.
This data structure is called 析合树, directly translated is cut join tree, but I think permutation tree is a better name. Honestly, after learning about it, it seems like a very niche data structure with very limited uses, but anyways here is the tutorial on it.
Thanks to dantoh and oolimry for helping me proofread.
Motivation
Consider this problem. We are given a permutation,$$$P$$$ of length $$$n$$$. A good range is a contiguous subsequence such that $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i = r-l$$$. This can be thought of the number of contiguous subsequence such that when we sort the numbers in this subsequence, we get contiguous values. Count the number of good ranges.
Example: $$$P=\{5,3,4,1,2\}$$$.
All good ranges are $$$[1,1], [2,2], [3,3], [4,4], [5,5], [2,3], [4,5], [1,3], [2,5], [1,5]$$$.
The $$$O(n^2)$$$ solution for this is using sparse table and checking every subsequence if it fits the given conditions. But it turns out we can speed this up using permutation tree to $$$O(n\log{n})$$$.
Definitions
A permutation $$$P$$$ of length $$$n$$$ is defined as:
- $$$|P|=n$$$
- $$$\forall i, P_i \in [1,n]$$$
- $$$\nexists i,j \in [1,n], P_i \ne P_j$$$
A good range is defined as a range, $$$[l,r]$$$ such that $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i = r-l$$$ or equivalently $$$\nexists x,z \in [l,r], y \notin [l,r], P_x<P_y<P_z$$$.
We denote a good range $$$[l,r]$$$ of $$$P$$$ as $$$(P, [l,r])$$$, and also denote the set of all good ranges as $$$I_g$$$.
Permutation Tree
So we want a structure that can store all good ranges efficiently.
Firstly, we can notice something about these good ranges. They are composed by the concatenation of other good ranges.
So the structure of the tree is that a node can have some children and the range of the parent is made up of the concatenation of the children's ranges.
Here is an example permutation. $$$P=\{9,1,10,3,2,5,7,6,8,4\}$$$.
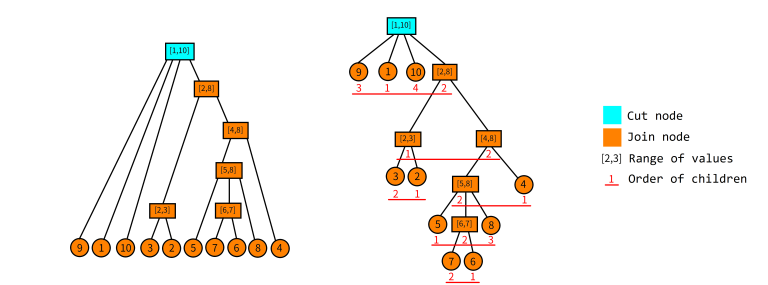
As we can see from the above image, every node represents a certain good range, where the values in the node represent the minimum and maximum values contains in this range.
Notice in this data structure, for any 2 nodes $$$[l_1,r_1]$$$ and $$$[l_2,r_2]$$$, WLOG $$$l_1 \leq l_2$$$, either $$$r_1<l_2$$$ or $$$r_2 \leq r_1$$$.
Definition of Cut Nodes and Join Nodes
We shall define some terms used in this data structure:
- Node range: For some node $$$u$$$, $$$[u_l,u_r]$$$ will describe the minimum and maximum value contained in the range the node represents
- Ranges of children: For some non-leaf node $$$u$$$, let the array $$$S_u$$$ denote the array of the ranges of its children. For example, the root node the above picture, $$$S_u$$$ is $$$\{[9,9],[1,1],[10,10],[2,8]\}$$$.
- Order of children: For some non-leaf node $$$u$$$, we can discretize the ranges in $$$S_u$$$. Again using the example of the root node, the order of its children is $$$\{3,1,4,2\}$$$, we will call this $$$D_u$$$.
- Join node: For some non-leaf node $$$u$$$, we call it a join node if $$$D_u=\{1,2,3,\cdots\}$$$ or $$$D_u=\{\cdots,3,2,1\}$$$. For simplicity we also consider all leaf nodes to be join nodes.
- Cut node: Any node that is not a join node.
Properties of Cut Nodes and Join Nodes
Firstly, we have this very trivial property. The union of all ranges of children is the node's range. Or in fancy math notation, $$$\bigcup_{i=1}^{|S_u|} S_u[i]=[u_l,u_r]$$$.
For a join node $$$u$$$, any contiguous subsequence of ranges of its children is a good range. Or, $$$\forall i,j,1 \leq i \leq j \leq |S_u|, \bigcup_{i=l}^{r} S_u[i]\in I_g$$$.
For a cut node $$$u$$$, the opposite is true. Any contiguous subsequence of ranges of its children larger than 1 is not a good range. Or, $$$\forall i,j,1 \leq i < j \leq |S_u|, \bigcup_{i=l}^{r} S_u[i]\notin I_g$$$.
The property of join nodes is not too hard to show by looking at the definition of what a join node is.
But the property of cut nodes is slightly harder to prove. A way to think about this is that for some cut node such that there is a subsequence of ranges bigger than 1 that form a good range, then that subsequence would have formed a range. This is a contradiction.
Construction of Permutation Tree
Now we will discuss a method to create the Permutation Tree in $$$O(n\log{n})$$$. According to a comment by CommonAnts, the creator of this data structure, a $$$O(n)$$$ algorithm exists, but I could not find any resources on it.
Brief overview of algorithm
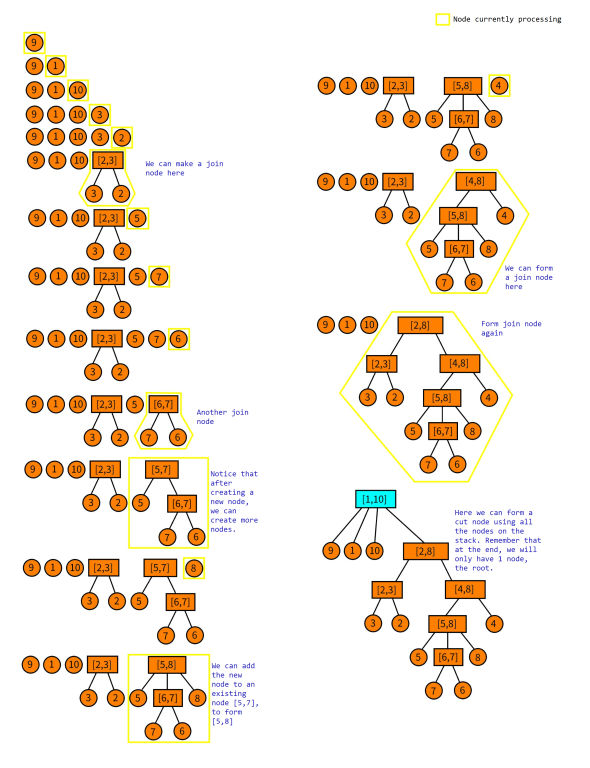
We process the permutation from left to right. We will also keep a stack of cut and join nodes that we have processed previously. Now let us consider adding $$$P_i$$$ to this stack. We firstly make a new node $$$[P_i,P_i]$$$ and call it the node we are currently processing.
- Check if we can add the currently processed as a child of the node on top of the stack.
- If we cannot, check if we can make a new parent node (this can either be a cut or join node) such that it contains some suffix of the stack and the current processed node as children.
- Repeat this process until we cannot do any more operations of type 1 or 2.
- Finally, push the currently processed node to the stack.
Notice that after processing all nodes, we will only have 1 node left on the stack, which is the root node.
Details of the algorithm
For operation 1, if we note that we can only do this if the node on top of the stack is a join node. Because if we can add this as a child to a cut node, then it contradicts the fact that no contiguous subsequence of ranges of children larger than 1 of a cut node can be a good range.
For operation 2, we need a fast way to find if there exists a good range such that we can make a new node from. There are 3 cases:
- We cannot make a new node.
- We can make a new join node. This new node has 2 children.
- We can make a new cut node.
Checking if there exists a good range
We have established for a good range $$$(P,[l,r])$$$ that $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i = r-l$$$.
Since $$$P$$$ is a permutation, we also have $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i \geq r-l$$$ for all ranges $$$[l,r]$$$.
Equivalently, we have $$$\max\limits_{l \leq i \leq r} P_i - \min\limits_{l \leq i \leq r} P_i - (r-l) \geq 0$$$, where we have equality only for good ranges.
Say that we are currently processing $$$P_i$$$. We define a value $$$Q$$$ for each range $$$[j,i], Q_j=\max\limits_{j \leq k \leq i} P_k - \min\limits_{j \leq k \leq i} P_k - (i-j),0< j \leq i$$$. Now we just need to check if there is some $$$Q_j=0$$$, where $$$j$$$ is not in the current node being processed.
Now we only need to know how to maintain this values of $$$Q_j$$$ quickly when we transition from $$$P_i$$$ to $$$P_{i+1}$$$. We can do this by updating the max and min values every time it changes. How can we do this?
Let's focus on updating the max values since updating the min values are similar. Let's consider when the max value will change. It changes every time $$$P_{i+1} > \max $$$. Let us maintain a stack of the values of $$$\max\limits_{j \leq k \leq i}P_k$$$, where we will store distinct values only. It can be seen that this stack is monotonically decreasing. When we add a new element to this stack, we will pop all elements in the stack which are smaller than it and update their maximum values using a segment tree range add update. This amortizes to $$$O(n)$$$ as each value is pushed into the stack once.
Do note to decrement all $$$Q_j$$$ by 1 since we are incrementing $$$i$$$ by 1.
Now that we can maintain all values of $$$Q_j$$$, we can simply check the minimum value of the range we are interested in using segment tree range minimum queries.
If we can make a new cut node, then we greedily try to make new cut node. We can do this by adding another node from our stack until our new cut node is valid.
Since the above may be confusing, here is a illustration of how the construction looks like.
Problems using Permutation Tree
Codeforces 526F – Pudding Monsters
CERC 17 Problem I – Instrinsic Interval
Codeforces 997E – Good Subsegments











Does anyone know any resources or the idea to speed up construction to $$$O(n)$$$?
I believe zscoder mentioned it in this comment. Don't understand Chinese however :(.
https://codeforces.com/blog/entry/70503#comment-549573
Ill try to translate what that blog says about the $$$O(n)$$$ part.
Ill just skip to the part about checking whether a good range exists. Suppose we have a range $$$[x,y]$$$, we want to find the smallest range $$$[l,r]$$$ such that $$$\forall k \in [\min\limits_{x \leq i \leq y} P_i,\max\limits_{x \leq i \leq y} P_i], k \in {P_l, P_{l+1}, \cdots , P_r}$$$.
Since we are fixing $$$y$$$, if $$$y<r$$$ then we cannot form a good range.
So every time we want to try to make a cut node, we traverse the stack using some failure function. What the failure function is that the first time we encounter $$$y<r$$$, we can set the failure function to point to $$$x$$$. So when we traverse the stack again later, we can skip a lot of nodes.
The blog says the correctness is trivial but I dont see how.
Anyways, you also need to find the range $$$[l,r]$$$ quickly. The blog says to use a RMQ which is usually have extra $$$O(n\log n)$$$ preprocessing, but apparently using something called 毛子算法 (I dont know what this is) the preprocessing can be $$$O(n)$$$.
But im not too sure about any of them... its 2 am right now and im really tired.
毛子 is a Chinese way to refer to Russians. I think 毛子算法 refers to the Four Russians algorithm.
As can be seen from this source, the Four Russians algorithm leads to an <O(N), O(1)> algorithm for the range minimum query problem.
Here is also a related problem https://www.codechef.com/problems/ARMYOFME
Thanks for this, I have tried to understand this before but couldn't as tutorial was Chinese and translation was not proper. Here, is similar problem https://www.codechef.com/MARCH20A/problems/GOODSEGS
I was waiting for posts about this topic. Thank you!
I posted this structure and mentioned the name “析合树” first in NOI Winter Camp 2019. :)
About $$$O(n)$$$ construction algorithm you can read the original slide(《刘承奥,简单的连续段数据结构,WC2019 营员交流》).
Hi !! Will u plz provide a hint for the problem https://codeforces.com/contest/997/problem/E using permutation tree .
Please help , I am unable to solve it
Use MO's algorithm. Now we need to solve problem of extending/shortening ranges. This can be done using 2k decomp+bsta on permutation tree.
Ive been quite busy these few days. Ill work out details later and update the blog then
Ok sir I will try .. But whenever u have time plz update this .. Its quite difficult topic . Thanks a lot
i finally ACed. Tried to do some MO's algorithm using the Q array but i think it constant time TLE. I couldn't make it pass so i just read benq's solution. he submitted 2 AC solutions
88692369 explictly uses permutation tree 88692987 involves a very clever use of the Q array
Sir , please explain ur solution a little bit . I saw it but could not understand it . I am able to think of only adding the elements when we move the curRight pointer but idk about the movement of left pointer and movement of right pointer to left . Please explain ur solution . Thanks a lot ....
Why downvotes ?? I was just asking for help ..
I believe benq's submit is O(nq) because he naively walks up from leaf to lca on each query.
his code runs in like 30s on my machine on the following case, (the permutation tree has height O(n) in this case)
I coded up the online O(n+q) to this problem 242495967 assuming I coded the linear build correctly. It uses brunomont's rmq https://codeforces.com/blog/entry/78931
solution outline: first count the good ranges in
lca(l,r)separatelythe main idea is consider the path from leaf
lto the node just beforelca(l,r)(found with https://codeforces.com/blog/entry/71567?#comment-559285)for each node
uon this path, we want to sum up the good ranges "to the right": e.g. if nodeuisi-th child ofpar[u], then for each subtree ofadj[par[u]][j]withj>iwe need sum up the good ranges in these subtreesthe trick is we can calculate
cnt_after[u]for each nodeu: as sum fromuto root of number of good ranges "to the right"Then for a query, we add to the answer
cnt_after[l] - cnt_after[child of lca(l,r), who is an ancestor of l]Sorry for the bothering 17 months later, but what exactly do you mean by 2k decomp, and bsta?
Couldn't find anything on those, unless BSTA is short for Augmented BST, and you mentioned the 2k decomp above as well as an LCA alternative so it got me curious :)
Thanks for posting the tutorial in english, it's been very useful!
From what I know, BSTA stands for Binary Search The Answer and 2k decomp is another name for binary lifting (as in you decompose the length in powers of 2).
i don't speak chinese
PQ tree
https://codeforces.com/blog/entry/69158?#comment-536295
seems like its different?
In the first problem, how are we counting number of zeros in a range using segment tree? Can anyone explain in details please? I am finding it difficult to understand that from the code.
U just need to count the number of minimums in the range as the minimum value will always be zero and this is a pretty standard problem . U can refer EDU section for this .
Thanks, that's what I needed to know.