| Codeforces Global Round 13 |
|---|
| Закончено |
Дан граф из $$$n$$$ строк и $$$10^6 + 2$$$ столбцов, где строки пронумерованы от $$$1$$$ до $$$n$$$, а столбцы от $$$0$$$ до $$$10^6 + 1$$$:
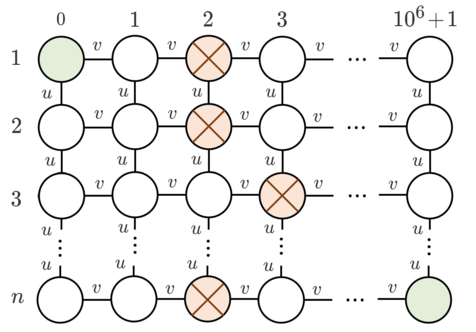
Обозначим вершину в строке $$$i$$$ и столбце $$$j$$$ как $$$(i, j)$$$.
Изначально для каждого $$$i$$$ строка $$$i$$$ содержит ровно одно препятствие — в вершине $$$(i, a_i)$$$. Вы хотите переместить несколько препятствий так, чтобы можно было достичь вершины $$$(n, 10^6+1)$$$, начав в вершине $$$(1, 0)$$$, перемещаясь по ребрам этого графа (нельзя проходить через вершины с препятствиями). Для перемещения одного препятствия на соседнюю по ребру свободную вершину нужны $$$u$$$ или $$$v$$$ монет:
- Если в вершине $$$(i, j)$$$ есть препятствие, можно использовать $$$u$$$ монет, чтобы переместить его в вершину $$$(i-1, j)$$$ или вершину $$$(i+1, j)$$$, если эта вершина существует, и в данный момент в ней нет препятствия.
- Если в вершине $$$(i, j)$$$ есть препятствие, то можно использовать $$$v$$$ монет, чтобы переместить его в вершину $$$(i, j-1)$$$ или вершину $$$(i, j+1)$$$, если эта вершина существует, и в данный момент в ней нет препятствия.
- Обратите внимание, что вы не можете перемещать препятствия за пределы сетки. Например, нельзя переместить препятствие с вершины $$$(1,1)$$$ в $$$(0,1)$$$.
Для лучшего понимания смотрите картинку выше.
Найдите минимальное количество монет, которое нужно потратить, чтобы можно было достичь вершины $$$(n, 10^6+1)$$$, начав в вершине $$$(1, 0)$$$, перемещаясь по ребрам этого графа, не проходя через вершины с препятствиями.
В первой строке содержится одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора входных данных содержит три целых числа $$$n$$$, $$$u$$$ и $$$v$$$ ($$$2 \le n \le 100$$$, $$$1 \le u, v \le 10^9$$$) — количество строк в графе и количества монет, необходимых для перемещения по вертикали и горизонтали соответственно.
Вторая строка каждого набора входных данных содержит $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^6$$$), где $$$a_i$$$ обозначает, что препятствие в $$$i$$$-й строке находится в вершине $$$(i, a_i)$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^4$$$.
Для каждого набора входных данных выведите единственное целое число — минимальное количество монет, которое нужно потратить, чтобы можно было достичь вершины $$$(n, 10^6+1)$$$, начав в вершине $$$(1, 0)$$$, перемещаясь по ребрам этого графа, не проходя через вершины с препятствиями.
Можно показать, что при ограничениях задачи всегда существует способ сделать такое путешествие возможным.
3 2 3 4 2 2 2 3 4 3 2 2 4 3 3 2
7 3 3
В первом примере два препятствия стоят в вершинах $$$(1, 2)$$$ и $$$(2,2)$$$. Вы можете передвинуть препятствие с $$$(2, 2)$$$ в $$$(2, 3)$$$, а затем в $$$(1, 3)$$$. Общая стоимость будет составлять $$$u+v = 7$$$ монет.
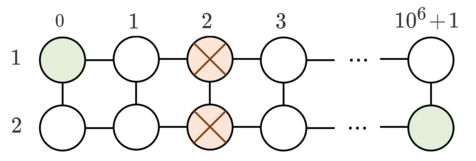
Во втором примере два препятствия стоят в $$$(1, 3)$$$ и $$$(2,2)$$$. Вы можете передвинуть препятствие с $$$(1, 3)$$$ в $$$(2, 3)$$$. Стоимость составляет $$$u = 3$$$ монеты.
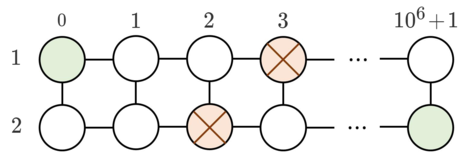
| Название |
|---|




