| Codeforces Round 865 (Div. 2) |
|---|
| Finished |
Ian and Mary are frogs living on lattice points of the Cartesian coordinate plane, with Ian living on $$$(0,0)$$$ and Mary living on $$$(a,b)$$$.
Ian would like to visit Mary by jumping around the Cartesian coordinate plane. Every second, he jumps from his current position $$$(x_p, y_p)$$$ to another lattice point $$$(x_q, y_q)$$$, such that no lattice point other than $$$(x_p, y_p)$$$ and $$$(x_q, y_q)$$$ lies on the segment between point $$$(x_p, y_p)$$$ and point $$$(x_q, y_q)$$$.
As Ian wants to meet Mary as soon as possible, he wants to jump towards point $$$(a,b)$$$ using at most $$$2$$$ jumps. Unfortunately, Ian is not good at maths. Can you help him?
A lattice point is defined as a point with both the $$$x$$$-coordinate and $$$y$$$-coordinate being integers.
The first line contains a single integer $$$t$$$ ($$$1 \le t \le 500$$$) — the number of test cases. The description of test cases follows.
The first and only line of each test case contains two integers $$$a$$$ and $$$b$$$ ($$$1\le a,b\le 10^9$$$) — the coordinates of the lattice point where Mary lives.
For each test case, print an integer $$$n$$$ ($$$1 \le n \le 2$$$) on the first line, denoting the number of jumps Ian uses in order to meet Mary. Note that you do not need to minimize the number of jumps.
On the $$$i$$$-th line of the next $$$n$$$ lines, print two integers $$$0 \le x_i,y_i \le 10^9$$$ separated by a space, denoting Ian's location $$$(x_i,y_i)$$$ after the $$$i$$$-th jump. $$$x_n = a$$$, $$$y_n = b$$$ must hold.
Ian's initial location and his locations after each of the $$$n$$$ jumps need not be distinct.
If there are multiple solutions, output any.
83 44 43 62 21 17 32022 20231000000000 1000000000
1 3 4 2 3 2 4 4 2 5 3 3 6 2 1 0 2 2 1 1 1 1 7 3 1 2022 2023 2 69420420 469696969 1000000000 1000000000
In the first test case:
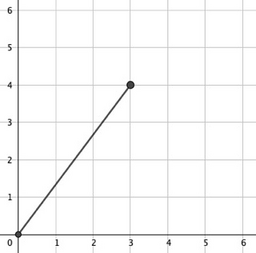
$$$(0,0) \to (3,4)$$$
In the second test case:
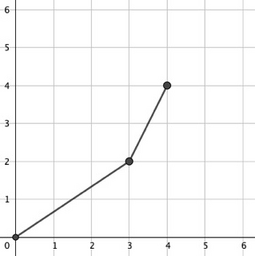
$$$(0,0) \to (3,2) \to (4,4)$$$
In the third test case:

$$$(0,0) \to (5,3) \to (3,6)$$$
| Name |
|---|




