Thanks for participating, and happy Easter!
1816A - Ian Visits Mary
Let us show that Ian can get to Mary within two moves. Indeed, consider $$$(x_1,y_1)$$$ and $$$(x_2,y_2)$$$ where $$$x_2-x_1=1$$$, since the value of the $$$x$$$-coordinates of a point lying on the segment joining $$$(x_1,y_1)$$$ and $$$(x_2,y_2)$$$, and is not at the endpoints, is strictly between $$$x_1$$$ and $$$x_2$$$, but there are no integers strictly between $$$x_1$$$ and $$$x_2$$$, the point must not be a lattice point. Similarly, no lattice points lie on the segment joining $$$(x_1,y_1)$$$ and $$$(x_2,y_2)$$$ with $$$y_2-y_1=1$$$ except for the endpoints. Therefore, Ian can jump from $$$(0,0)$$$ to $$$(x-1,1)$$$ to $$$(x,y)$$$.
#include<bits/stdc++.h>
using namespace std;
void solve(){
int a,b;
cin >> a >> b;
cout << 2 << "\n" << a-1 << ' ' << 1 << "\n" << a << ' ' << b << "\n";
}
int main(){
int t;
cin >> t;
while(t--){
solve();
}
}
Originally, the problem asks you for the minimal amount of steps, which requires gcd. Since it would be too hard, we had a quite last-minute change to the current statement.
1816B - Grid Reconstruction
Consider the parity (odd/even) of $$$i+j$$$. What do you observe?
Observe that $$$a_{i,j}$$$ will be added if $$$(i+j)$$$ is even, and will be subtracted otherwise. This forms a checkered pattern.
Obviously, it is optimal for all values that will be added to be strictly larger than all values that will be subtracted. Also, the difference between the value of adjacent grids should be almost equal (by some definition of almost).
We construct array $$$a$$$ as follows:
- $$$a_{1,1} = 2n-1$$$ and $$$a_{2,n} = 2n$$$
- For $$$2 \leq i \leq n$$$ and $$$i$$$ is even, $$$a_{1,i} = i$$$ and $$$a_{2,i-1} = i - 1$$$
- For $$$2 \leq i \leq n$$$ and $$$i$$$ is odd, $$$a_{1,i} = n + i - 1$$$ and $$$a_{2,i-1} = n + (i - 1) - 1$$$
For example, when $$$n=10$$$, the output will be
19 2 12 4 14 6 16 8 18 10
1 11 3 13 5 15 7 17 9 20
(This is a very informal proof. See "Proof" below for a formal proof.)
First of all, due to the checkered pattern, $$$a_{1,1}, a_{2,2}, a_{1,3}, \cdots, a_{2,n}$$$ should be filled with $$$n+1, n+2, n+3, \cdots, 2n$$$, and $$$a_{2,1}, a_{1,2}, a_{2,3}, \cdots, a_{1,n}$$$ should be filled with $$$1, 2, 3, \cdots, n$$$. In particular, $$$a_{1,1}$$$ and $$$a_{2,n}$$$ should be $$$2n-1$$$ and $$$2n$$$.
Next, as we are trying to maximise the minimum, the difference between paths shouldn't be large (since the minimum path will be smaller if the difference is larger). Notice that a path consists of a prefix of $$$a_1$$$ and a suffix of $$$a_2$$$, and the difference between $$$2$$$ adjacent paths is $$$\pm (a_{1,k} - a_{2,k-1})$$$ (depending on the parity of $$$k$$$). It is optimal for the difference to be as small as possible (which is $$$1$$$).
Finally, it is optimal that $$$a_{1,k} - a_{2,k-1}$$$ stays constant in the whole array. If they are different, the difference between $$$2$$$ paths (not adjacent) will be larger than $$$1$$$, which is suboptimal.
Consider the cost of the top right path and bottom left path.
The cost of the top right path is $$$a_{1,1} - a_{1,2} + a_{1,3} - \cdots - a_{1,n} + a_{2,n}$$$.
The cost of the bottom right path is $$$a_{1,1} - a_{2,1} + a_{2,2} - a_{2,3} + ... + a_{2,n}$$$.
Summing both values, we get
$$$a_{1,1} + a_{2,n} + ((a_{1,1} - a_{1,2} + a_{1,3} - a_{1,4} + ... - a_{1,n}) + (-a_{2,1} + a_{2,2} - a_{2,3} + ... + a_{2,n}))$$$
which is equal to
$$$a_{1,1} + a_{2,n} + ((a_{1,1} + a_{2,2} + a_{1,3} + a_{2,4} + \cdots + a_{2,n}) - (a_{2,1} + a_{1,2} + a_{2,3} + a_{1,4} + \cdots + a_{1,n}))$$$
This value attains maximum when $$$a_{1,1} = 2n$$$, $$$a_{2,n} = 2n-1$$$, $$$(a_{1,1} + a_{2,2} + a_{1,3} + a_{2,4} + \cdots + a_{2,n}) = ((n+1) + (n+2) + (n+3) + \cdots + 2n)$$$ and $$$(a_{2,1} + a_{1,2} + a_{2,3} + a_{1,4} + \cdots + a_{1,n}) = (1 + 2 + 3 + \cdots + n)$$$, which is $$$(2n + (2n - 1) + (\frac{(n)((n+1)+2n)}{2}) - (\frac{(n)(1+n)}{2})) = (n^2 + 4n - 1)$$$.
Therefore, the upper bound for the maximum cost is $$$\lfloor \frac{n^2 + 4n - 1}{2} \rfloor = \frac{1}{2}n^2 + 2n - 1$$$. We will now show that the construction above meets the upper bound.
Let $$$P_k$$$ be the cost of the path $$$a_{1,1}, a_{1,2}, a_{1,3}, \cdots, a_{1,k}, a_{2,k}, a_{2,k+1}, \cdots, a_{2,n}$$$.
Observe that $$$P_k - P_{k-1} = (-1)^k(a_{1,k} - a_{2,k-1}) = (-1)^k$$$, as the paths differ by exactly $$$2$$$ grids and $$$a_{1,k} - a_{2,k-1} = 1$$$ (from the above construction).
Calculating $$$P$$$,
$$$P_1 = (2n - 1) - 2 + (n + 2) - 4 + (n + 4) - \cdots - (n - 2) + 2n = (2n - 1) + (n)(\frac{n}{2} - 1) - n + 2n = \frac{1}{2}n^2 + 2n - 1$$$
$$$P_2 = P_1 + (-1)^2 = \frac{1}{2}n^2 + 2n$$$
$$$P_3 = P_2 + (-1)^3 = \frac{1}{2}n^2 + 2n - 1$$$
$$$\cdots$$$
Therefore, $$$min(P) = \frac{1}{2}n^2 + 2n - 1$$$, which achieves the upper bound.
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
int ans[3][n + 1];
ans[1][1] = 2 * n - 1;
ans[2][n] = 2 * n;
for (int i = 2; i <= n; i++) {
if (i % 2 == 0) {
ans[1][i] = i;
ans[2][i - 1] = i - 1;
} else {
ans[1][i] = n + (i - 1);
ans[2][i - 1] = n + (i - 1) - 1;
}
}
for (int i = 1; i <= 2; i++) {
for (int j = 1; j <= n; j++) {
cout << ans[i][j] << (j == n ? '\n' : ' ');
}
}
}
}
Can you find a construction for a $$$n \times n$$$ grid (and give a formal proof)? (We don't have a solution)
1815A - Ian and Array Sorting
Consider difference array $$$[a_2-a_1,a_3-a_2,...,a_n-a_{n-1}]$$$. If the original array is non-decreasing, what properties does the difference array have?
Operations to the original array correspond to what operations in the difference array?
We consider the difference array $$$b_i=a_{i+1}-a_i$$$ ($$$1\le i\le n-1$$$). Then the original array is non-decreasing if and only if all elements of the difference array is non-negative. We can see that either $$$b_i$$$ is increased by $$$1$$$ and $$$b_{i+2}$$$ is decreased by $$$1$$$ or vice versa for $$$1\le i\le n-3$$$, $$$b_2$$$ is increased or decreased by $$$1$$$ or $$$b_{n-2}$$$ is increased or decreased by $$$1$$$.
If $$$n$$$ is odd, then $$$n-2$$$ is odd. What we can do is to increase $$$b_2$$$ and $$$b_{n-2}$$$ enough number of times, and then do $$$b_i$$$ increase by $$$1$$$ and $$$b_{i+2}$$$ decrease by $$$1$$$ or vice versa enough times to distribute the values to other elements of $$$b$$$. Doing this, we can make all of the elements of $$$b$$$ non-negative, which is what we want. So we output 'YES' no matter what for odd $$$n$$$.
For even $$$n$$$, $$$n-2$$$ is even. So by increasing $$$b_2$$$ and $$$b_{n-2}$$$ enough number of times, then distributing, we can only ensure that the elements of $$$b$$$ with even indices are non-negative. Since the only operation that affects odd indices is increasing $$$b_i$$$ by $$$1$$$ and decreasing $$$b_{i+2}$$$ by $$$1$$$ or vice versa, we can see that the sum of the elements of $$$b$$$ with odd indices will not change. If the sum of the elements of $$$b$$$ with odd indices is at least $$$0$$$, we can distribute the values such that in the end, all of them are non-negative, so we should output 'YES'. But if the sum of elements of $$$b$$$ with odd indices is negative, there must exist a negative $$$b_i$$$ in the end, and we should output 'NO'.
#include<bits/stdc++.h>
using namespace std;
void solve(){
int n;
cin >> n;
int arr[n];
long long int altsum=0;
for(int i=0;i<n;i++){
cin >> arr[i];
if(i%2==0){
altsum-=arr[i];
}
else{
altsum+=arr[i];
}
}
if(n%2==1||altsum>=0){
cout << "YES\n";
}
else{
cout << "NO\n";
}
return;
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int t;
cin >> t;
while(t--){
solve();
}
}
1815B - Sum Graph
Consider using a type 1 operation on $$$x=n+1$$$ and $$$x=n+2$$$. What do you notice?
The resulting graph, after performing type 1 operations according to hint 1, will be a chain (e.g. when $$$n=6$$$, it should look like $$$1 - 6 - 2 - 5 - 3 - 4$$$). Now, try to figure out a position $$$k$$$ such that node $$$p_k$$$ is one of the endpoints of the chain. Once you figure that out, how can you make use of this to solve the full problem?
There are many ways to solve this problem. My original solution is rather difficult to implement correctly, and a bit complicated. During round testing, tester rsj found an alternative solution, which is, in my opinion, one that's a lot easier to understand and implement.
Firstly, use a type 1 operation on $$$x=n+1$$$ and $$$x=n+2$$$ (or you can do $$$x=n$$$ and $$$x=n+1$$$). Then, the graph should look like a chain (e.g. when $$$n=6$$$, it should look like $$$1 - 6 - 2 - 5 - 3 - 4$$$). Note that there are actually two edges between each pair of directly connected nodes, but it is irrelevant to the task.
Next, use a type 2 query on all pairs of $$$(1,i)$$$ where $$$2 \le i \le n$$$. Take the maximum of the query results. Let $$$k$$$ be one of the values such that the query result of $$$(1,k)$$$ is maximum among all $$$(1,i)$$$. It is easy to see that, node $$$p_k$$$ is one of the endpoints of the chain.
Afterwards, use a type 2 query on all pairs of $$$(k,i)$$$ where $$$1 \le i \le n$$$ and $$$i \ne k$$$. Since node $$$p_k$$$ is an endpoint of the chain, all the query results are distinct and you can recover the exact node that each query result corresponds to.
A problem arises that it is unclear about which endpoint node $$$p_k$$$ actually is. But this issue can be solved easily: since the problem allows outputting two permutations that can be $$$p$$$, just try both endpoints and output the corresponding permutations.
In total, $$$2$$$ type 1 operations and $$$2n-2$$$ type 2 operations are used, which sums up to $$$2n$$$ operations. As stated in the sample description, you don't even need any operations when $$$n=2$$$. It is also easy to see that the actual number of operations required is $$$2n-1$$$ since there is a pair of duplicate type 2 operations, but we allow duplicating the operation anyway.
#include <bits/stdc++.h>
using namespace std;
void solve(int tc) {
int n; cin >> n;
cout << "+ " << n+1 << endl;
cout << "+ " << n+2 << endl;
int l = 1, r = n;
int ord[n+1];
for(int i=1; i<=n; i++) {
if(i & 1) ord[i] = l++;
else ord[i] = r--;
}
int dist1[n+1];
dist1[1] = 0;
int ma = 0, id;
for(int i=2; i<=n; i++) {
cout << "? 1 " << i << endl;
cin >> dist1[i];
if(dist1[i] > ma) {
ma = dist1[i];
id= i;
}
}
int p[n+1], q[n+1];
p[id] = ord[1];
q[id] = ord[n];
for(int i=1; i<=n; i++) {
if(i != id) {
cout << "? " << id << " " << i << endl;
int x;
cin >> x;
p[i] = ord[x+1];
q[i] = ord[n-x];
}
}
cout << "!";
for(int i=1; i<=n; i++) cout << " " << p[i];
for(int i=1; i<=n; i++) cout << " " << q[i];
cout << endl;
}
int32_t main() {
int t = 1; cin >> t;
for(int i=1; i<=t; i++) solve(i);
}
Try to solve the problem using at most $$$n + \left \lfloor \frac{n}{2} \right \rfloor + 2$$$ queries.
Refer to this comment. Thanks to -1e11 and FatihSolak for the solution. (To pass this problem using this solution, optimizations for $$$n=2$$$ are needed, as mentioned in the editorial section.)
Another way of solving the harder version provided by sysia: refer to this comment.
1815C - Between
Construct a graph with $$$n$$$ vertices and add a directed edge $$$a \rightarrow b$$$ if between every two $$$a$$$ there must be a $$$b$$$.
Let $$$v_a$$$ be the number of occurrences of $$$a$$$. The key observation is that if $$$a \rightarrow b$$$, then $$$v_{a} \leq v_{b} + 1$$$.
Suppose $$$a_k \rightarrow a_{k-1} \rightarrow \cdots a_1$$$ is a directed path, where $$$a_1 = 1$$$. Then since $$$v_1 = 1$$$, we must have
Unable to parse markup [type=CF_MATHJAX]
. In other words, $$$v_s \leq d_s $$$. where $$$d_s$$$ is one plus the length of the shortest directed path from $$$s$$$ to $$$1$$$.Therefore, the total array length does not exceed $$$\sum_{i=1}^{n} d_i$$$. We claim that we can achieve this.
It is easy to calculate the $$$d_s$$$ by a BFS. Let $$$T_i$$$ consists of vertices $$$x$$$ such that $$$v_x = s$$$. Let $$$M$$$ the largest value of $$$d_i$$$ among all $$$i \in {1,2\cdots n}$$$. Consider
where for each $$$i$$$, vertices in various occurrences of $$$T_i$$$ must be arranged in the same order.
It is easy to check that this construction satisfies all the constraints and achieve the upper bound $$$\sum_{i=1}^{n} d_i$$$. Thus, this output is correct.
The sequence can be arbitrarily long if and only if there is some $$$v$$$ that does not have a path directed to $$$1$$$. To see this, let $$$S$$$ be the set of vertices that do not have path directed to $$$1$$$, then the following construction gives an arbitrarily long output that satisfy all constraints:
#include<bits/stdc++.h>
using namespace std;
void solve(){
int n,m;
cin >> n >> m;
vector <int> adj[n+1];
int occ[n+1];
occ[1]=1;
for(int i=0;i<m;i++){
int x,y;
cin >> x >> y;
adj[y].push_back(x);
}
for(int i=2;i<=n;i++){
occ[i]=0;
}
queue <int> bfs;
bfs.push(1);
while(bfs.size()>0){
int f=bfs.front();
bfs.pop();
for(int i=0;i<adj[f].size();i++){
if(occ[adj[f][i]]==0){
occ[adj[f][i]]=occ[f]+1;
bfs.push(adj[f][i]);
}
}
}
vector <int> v[n+1];
int ans=0;
for(int i=1;i<=n;i++){
if(occ[i]==0){
cout << "INFINITE\n";
return;
}
v[occ[i]].push_back(i);
ans+=occ[i];
}
cout << "FINITE\n" << ans << endl;
for(int i=n;i>=1;i--){
for(int j=n;j>=i;j--){
if(i%2!=j%2){
continue;
}
for(int k=0;k<v[j].size();k++){
cout << v[j][k] << ' ';
}
}
}
for(int i=2;i<=n;i++){
for(int j=n;j>=i;j--){
if(i%2!=j%2){
continue;
}
for(int k=0;k<v[j].size();k++){
cout << v[j][k] << ' ';
}
}
}
cout << endl;
return;
}
int main(){
int t;
cin >> t;
while(t--){
solve();
}
}
1815D - XOR Counting
The cases when $$$m=1$$$ and $$$m\ge3$$$ are relatively much easier than when $$$m=2$$$.
When $$$m=2$$$, perform an $$$O(\log n)$$$ DP on answer. Notice we have to DP another thing as well. What is it?
If $$$m=1$$$, it is clear that we only can have $$$a_1=n$$$ so the answer is $$$n$$$.
If $$$m\ge3$$$, $$$\left[x,\frac{n-x}2,\frac{n-x}2,0,0,...\right]$$$ gives a xor of $$$x$$$, so all $$$x$$$ with the same parity as $$$n$$$ and at most $$$n$$$ can be achieved. Notice xor and sum are identical in terms of parity, and $$$a\oplus b\le a+b$$$. So these restrict that only values of $$$x$$$ that has same parity with $$$n$$$ and is at most $$$n$$$ is possible as a result of the xor. Therefore, we can use $$$O(1)$$$ to calculate the sum of all non-negative integers at most $$$n$$$ and have same parity as $$$n$$$.
It remains to handle the case when $$$m=2$$$. We create the functions $$$f(n)$$$ and $$$g(n)$$$, where $$$f(n)$$$ is the sum of all possible values of the xor and $$$g(n)$$$ counts the number of all possible values of the xor. We then consider the following:
If $$$n$$$ is odd, then one of $$$a_1,a_2$$$ is even and the other is odd. WLOG assume $$$a_1$$$ is even and $$$a_2$$$ is odd. Then we let $$$a_1'=\frac{a_1}2$$$ and $$$a_2'=\frac{a_2-1}2$$$. We can see that $$$a_1'+a_2'=\frac{n-1}2$$$ and $$$a_1\oplus a_2=2(a_1'\oplus a_2')+1$$$. Hence we know that $$$g(n)=g\left(\frac{n-1}2\right)$$$, and $$$f(n)=2f\left(\frac{n-1}2\right)+g\left(\frac{n-1}2\right)$$$.
If $$$n$$$ is even, there are two cases. If $$$a_1$$$ and $$$a_2$$$ are both even, we let $$$a_1'=\frac{a_1}2$$$ and $$$a_2'=\frac{a_2}2$$$. We can see that $$$a_1'+a_2'=\frac{n}2$$$ and $$$a_1\oplus a_2=2(a_1'\oplus a_2')$$$. If $$$a_1$$$ and $$$a_2$$$ are both odd, we let $$$a_1'=\frac{a_1-1}2$$$ and $$$a_2'=\frac{a_2-1}2$$$. We can see that $$$a_1'+a_2'=\frac{n}2-1$$$ and $$$a_1\oplus a_2=2(a_1'\oplus a_2')$$$. Hence we know that $$$f(n)=2f\left(\frac{n}2\right)+2f\left(\frac{n}2-1\right)$$$, and $$$g(n)=g\left(\frac{n}2\right)+g\left(\frac{n}2-1\right)$$$.
So we can simply DP. It can be seen that the time complexity is $$$O(\log n)$$$ per test case, so we are done.
#include<bits/stdc++.h>
using namespace std;
unordered_map <long long int,long long int> npos,spos;
const int MOD=998244353;
long long int solve(long long int n){
if(npos[n]!=0){
return spos[n];
}
if(n%2==1){
solve(n/2);
npos[n]=npos[n/2];
spos[n]=spos[n/2]*2+npos[n/2];
spos[n]%=MOD;
}
else{
solve(n/2); solve(n/2-1);
npos[n]=npos[n/2]+npos[n/2-1];
spos[n]=(spos[n/2]+spos[n/2-1])*2;
spos[n]%=MOD;
}
return spos[n];
}
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
npos[0]=1;
spos[0]=0;
int t;
cin >> t;
while(t--){
long long int n,m;
cin >> n >> m;
if(m==2){
cout << solve(n) << endl;
}
else if(m==1){
cout << n%MOD << endl;
}
else if(n%2==0){
cout << (((n/2)%MOD)*((n/2+1)%MOD))%MOD << endl;
}
else{
cout << (((n/2+1)%MOD)*((n/2+1)%MOD))%MOD << endl;
}
}
}
1815E - Bosco and Particle
If the oscillator string is periodic, what should we do?
Use the case when $$$n=1$$$ to help you calculate the answer.
Observe that whole process is periodic.
Note that the process is reversible. If you are in some state $$$s$$$, consisting of position of the particle and the current state position of each oscillator, you can decide the next state and the previous state. This implies the state transition graph is a permutation, so it decomposes into cycles.
Firstly, we can easily see that removing cycles for the oscillator strings does not affect the answer. To help us calculating the answer easier, we have to remove cycle. You can remove cycle using any fast enough string algorithm such as KMP.
It is not difficult to see that if all strings are non-periodic, then being periodic with respect to the particle position $$$x$$$ is the same as being periodic with respect to both $$$x$$$ and all oscillator states.
Let $$$a_i$$$ be the number of times the particle hits oscillator $$$i$$$ when moving downwards and $$$b_i$$$ be the number of times the particle hits oscillator i when moving upwards in each cycle.
For each oscillator $$$i$$$, consider the case when $$$n=1$$$ and oscillator $$$i$$$ is the only oscillator. Let $$$a'_i$$$ be the number of times the particle hits oscillator $$$i$$$ when moving downwards and $$$b'_i$$$ be the number of times the particle hits the oscillator $$$i$$$ when moving upwards in each cycle.
Then we must have $$$a_i=ka'_i$$$ and $$$b_i=kb'_i$$$ for some positive integer k. Also, we must have $$$a_i=b_{i-1}$$$ as the number of times the particle goes from oscillator $$$i-1$$$ to oscillator $$$i$$$ is same as the number of times the particle goes from oscillator $$$i$$$ to oscillator $$$i-1$$$. It can be shown that the smallest integers $$$a_i$$$ and $$$b_i$$$ satisfying the above constraints must be the period.
We can calculate the the smallest such integers, by factoring each $$$k$$$ and maintain the primes. In other words, we can separately consider the $$$p$$$-adic valuation of the $$$a'_i$$$'s and $$$b'_i$$$'s to get the $$$p$$$-adic valuation of $$$a_i$$$'s and $$$b_i$$$'s for each prime. Below is a visualisation:
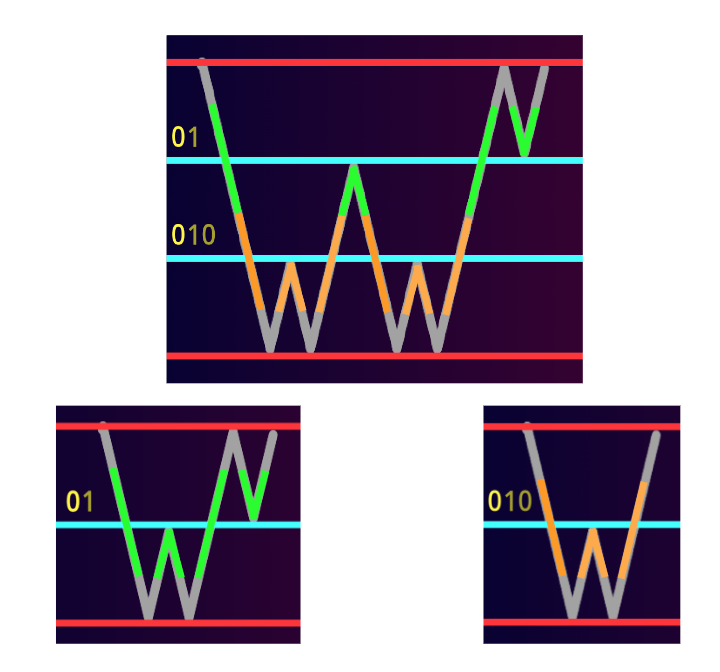
Notice the answer is $$$2(a_1+a_2+...+a_n+b_n)$$$, which can be easily calculated. So we are done.
#include<bits/stdc++.h>
using namespace std;
vector <int> prime;
bool p[1000001];
const long long int mod=998244353;
void init(){
p[1]=0;
for(int i=2;i<=1000000;i++){
p[i]=1;
}
for(int i=2;i<=1000000;i++){
if(p[i]){
prime.push_back(i);
}
for(int j=i;j<=1000000;j+=i){
p[j]=0;
}
}
return;
}
long long int bigmod(long long int n,long long int k){
long long int pown=n,ans=1;
while(k>0){
if(k%2){
ans*=pown;
ans%=mod;
}
pown*=pown;
pown%=mod;
k/=2;
}
return ans;
}
int vp(long long int n,int p){
int ans=0;
if(n==0){
return 10000000;
}
while(n%p==0){
n/=p;
ans++;
}
return ans;
}
string rpc(string str){
int i=0;
int len=str.length();
int j=-1;
int nextval[len];
nextval[i]=-1;
while (i<len){
if (j==-1||str[i]==str[j]){
i++;
j++;
nextval[i]=j;
}
else
j=nextval[j];
}
if ((len)%(len-nextval[len])==0) return str.substr(0,len-nextval[len]);
else return str;
}
int main(){
init();
int n;
cin >> n;
int lim=n;
pair<int,int> arr[n];
for(int i=0;i<n;i++){
string s;
cin >> s;
s=rpc(s);
int x=0,y=0,ptr=0;
bool b=true;
do{
if(b){
x++;
}
else{
y++;
}
if(s[ptr]=='0'){
b=1-b;
}
ptr++;
ptr%=s.length();
}while(!b||(ptr!=0));
arr[i]={x,y};
if(y==0&&lim==n){
lim=i;
}
}
long long int times[n+1];
for(int i=0;i<=n;i++){
times[i]=1;
}
for(int i=0;i<prime.size();i++){
int p=prime[i],curl=0,curr=0,difp[lim+1]={0};
for(int j=1;j<=lim;j++){
int l=vp(arr[j-1].first,p);
int r=vp(arr[j-1].second,p);
if(curr<l){
curl+=(l-curr);
curr=r;
}
else{
curr+=(r-l);
}
difp[j]=r-l;
}
int cur=curl;
for(int j=0;j<=lim;j++){
cur+=difp[j];
times[j]*=bigmod(p,cur);
times[j]%=mod;
}
}
long long int ans=0;
for(int i=0;i<=lim;i++){
ans+=times[i];
ans%=mod;
}
cout << (2*ans)%mod << endl;
}
1815F - OH NO1 (-2-3-4)
Go through from vertex $$$1$$$ through $$$n$$$ and decided their final weights in this order. When deciding the weights for $$$v$$$ , make sure it is different from $$$w$$$ if $$$w < v$$$ and $$$v$$$ is adjacent to $$$w$$$. Ignore vertices $$$x$$$ where $$$x$$$ is adjacent to $$$v$$$ but have $$$x > v$$$.
If there are at least $$$d+1$$$ options to take from, and $$$d$$$ of them are not available, then there is still some option to take.
Let's try to decide the final weights of $$$1$$$ through $$$n$$$ in this order. For a triangle $$$a<b<c$$$, we call $$$a$$$ the first vertex, $$$b$$$ the second vertex, $$$c$$$ the third vertex. Consider each triangle individually, if we can achieve the following task then we are done: By only adjusting edges of this triangle:
- There is at least one option for the first vertex
- After fixing a particular option for the first vertex, there are at least two options for the the second vertex
- After fixing particular options for the first two vertices, there are at least three options for the third vertex
To see this is enough: Suppose a vertex $$$v$$$ is in $$$A$$$ triangles as the first vertex, $$$B$$$ triangles as the second vertex, and $$$C$$$ triangles as the third vertex. It is not difficult to see $$$v$$$ have exactly $$$B + 2 \times C$$$ neighbours that are of smaller index, and there are at least $$$B+ 2\times C+ 1$$$ options.
Finally, by using the following specific edge weights, the goal can be achieved:
- $$$1,4,4$$$ gives weights $$$5,5,8$$$
- $$$2,3,3$$$ gives weights $$$5,5,6$$$
- $$$3,2,2$$$ gives weights $$$5,5,4$$$
- $$$1,4,3$$$ gives weights $$$5,4,7$$$
- $$$2,3,2$$$ gives weights $$$5,4,5$$$
- $$$3,2,1$$$ gives weights $$$5,4,3$$$
These numbers aren't exactly just completely random. You can see that they are composed of two components: A $$$(+1,-1,-1)$$$ part and a $$$(0,0,-1)$$$ part. Upto two copies of the first option and upto one copy of the second option have been used.
There is also a simple solution in this specific case where $$$G$$$ consists of triangles and use only weights 1,2,3.
This is a special case of 1-2-3 conjecture, which states that the above statement holds for arbitrary graph and using only the weights 1,2,3 (and no 4). Recently (March 2023) it has a claimed proof. The claimed algorithm is far from a linear time algorithm however.
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fi first
#define se second
const ll mod=998244353;
const int N=2e6+1;
ll n,m;
vector<pair<int,int> >adj[N];
array<int,3>e[N];
array<int,3>f[N];
ll a[N],b[N];
pair<int,int>vis[10000005];
void solve(){
cin >> n >> m;
for(int i=1; i<=n ;i++){
adj[i].clear();
}
for(int i=1; i<=n ;i++){
cin >> a[i];
}
for(int i=1; i<=m ;i++){
for(int j=0; j<3 ;j++){
cin >> e[i][j];
adj[e[i][j]].push_back({i,j});
}
f[i][0]=3;
f[i][1]=1;
f[i][2]=1;
a[e[i][0]]+=f[i][0]+f[i][2];
a[e[i][1]]+=f[i][1]+f[i][0];
a[e[i][2]]+=f[i][2]+f[i][1];
}
for(int i=1; i<=n ;i++){
for(auto c:adj[i]){
for(int d=0; d<c.se ;d++){
vis[a[e[c.fi][d]]]={c.fi,d};
}
}
while(vis[a[i]].fi!=0){
int ed=vis[a[i]].fi;
if(i==e[ed][1]){
a[i]++;
a[e[ed][2]]++;
f[ed][1]++;
}
else{
a[i]+=2;
f[ed][0]--;
f[ed][1]++;
f[ed][2]++;
}
}
for(auto c:adj[i]){
for(int d=0; d<c.se ;d++){
vis[a[e[c.fi][d]]]={0,0};
}
}
}
for(int i=1; i<=m ;i++){
cout << f[i][0] << ' ' << f[i][1] << ' ' << f[i][2] << '\n';
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int t;cin >> t;while(t--) solve();
}










In problem D2C / D1A's Editorial, please correct the following line
For even n, n−2 is odd...what;s s in Let Ti consists of vertices x such that vx=s .
I think it should be "Let T_i consists of vertices x such that v_x = i". In other words, T_i consists of all the vertices which shortest distance to 1 is (i-1). It is also true that such x will appear i number of times in the final sequence.
A slightly simpler solution of 1815A:
The answer is "NO" if and only if n is even and the alternating sum of the elements of A is positive. Obviously the alternating sum is constant and this linear condition is the only condition on elements of A (we can add n-1 linearly independent vectors to A any number of times each). So we can transform A into any other array with the same alternating sum. The only situation where such an array does not exist is when n is even and the alternating sum is strictly positive.
AC submission — Java — iterative
AC submission — Java — recursive
I posted this on the main blog but I realized that maybe its better to post it here.
Can someone please explain proof of B in editorial in more detail?
In particular, I would like to know what does it mean lowerbound for maximum cost and how do we, from the observations in proof before that, conclude that this is the value of the lowerbound.
In task we need to construct the grid such that minimum cost over all paths is maximized. So I think in order to prove that some construction satisfies the requirements we need to find value C(n) such that for every placement of integers on the grid minimum cost among all paths in the grid is <= C(n). Then we need to show that for our construction minimal cost equals C(n). Am I wrong?
Editorial contains the formal proof. My intuition for the problem using n = 12 as example is below. To place {1,2,3,4,5,6,7,8,9,10,11,12} into 12 spots, among which 6 has positive contribution to the alternating sums. It always makes sense to place {7,8,9,10,11,12} into the positive spots.
As v[1][1] and v[2][6] are both positive and always included, it always makes sense to place {12,11} into these two spots. A path would pass exactly one of v[1][3] or v[2][2], so it makes sense to place (10,9) into these two spots. I end up placing these 5 pairs (10,9)(8,7)(6,5)(4,3)(2,1) the way below with bigger value in second row. The intuition happens to be right.
Thanks for this I was struggling with how could this solution be thought of intuitively
I'm struggling to understand Div2D's example. How does
[1 2 3 4 5 6]comply with the query about $$$p_1$$$ and $$$p_3$$$? The distance between nodes 1 and 3 is 2 in the graph at that time.To be clear, the example's description does not mean that we have ruled out
[2 3 1 5 4 6]for instance?The example is correct by coincidence. It does not rule out other possibilities.
This is common for interactive problems. The example mostly boils down to randomly guessing to avoid hinting you about the solution.
You guess 2 permutations and only 1 of them needs to be correct. In this example the first one $$$(1,4,2,5,3,6)$$$ is correct, so it doesn't matter whether the second one $$$(1,2,3,4,5,6)$$$ is consistent with earlier queries.
I see, thanks! But the example's solution had not figured out the permutation with certainty, right?
I solved Div1D without noticing the pattern for $$$m\geq 3$$$. This DP is still $$$O(\log n)$$$ but works for all $$$m\geq 1$$$.
Let $$$s(l,r)$$$ be the sum of all possible XOR values, and $$$c(l,r)$$$ be the number of possible XOR values, when $$$l\leq a_1+\dots+a_m \leq r$$$. The answer to the original problem is $$$s(n,n)$$$.
If we additionally require the lowest bit of the XOR value must be 0, the set of possible sums are $$$2\lceil\frac{l}{2}\rceil,2(\lceil\frac{l}{2}\rceil+1),\dots,2\lfloor\frac{r}{2}\rfloor$$$, and the number of 1s in the lowest bits of $$$a_1,\dots,a_m$$$ can be $$$0,2,4,\dots,2\lfloor\frac{m}{2}\rfloor$$$. Notice that both of them are set of integers equally spaced by 2. Thus by right shifting all numbers by 1 (that is, removing their lowest bits), we obtain a subproblem where the set of possible sums is again a contiguous interval. More precisely $$$\lceil\frac{l}{2}\rceil-\lfloor\frac{m}{2}\rfloor\leq a_1+\dots+a_m \leq\lfloor\frac{r}{2}\rfloor$$$. The contribution of this subproblem is
Similarly for the case where the lowest bit of XOR value must be 1, we have
We can inductively show that all $$$l$$$'s and $$$r$$$'s for all states at the same depth of the recursion differs by at most 1 from each other. Thus the number of states at each level is bounded by a constant, and the recursion will only involve $$$O(\log n)$$$ distinct states.
For Div1B/Div2D I have a working algorithm working on my local computer, but the OJ is declining it for some reason. I've tried doing a custom test with what the input would have been and it worked just as intended, but it is still declining it for some reason.
It keeps giving me "wrong answer Wrong + operation format: x = 1 which is not between 2 and 2*n inclusive :( (test case 2)", but I am pretty sure my code doesn't print a "+ 1" unless n=1. Since the boundary for n is n>=2, it should never happen.
Could anyone help me out with what I messed up so I can avoid this on future interactive problems?
I'm dumb I wasn't getting input to see if my final guess was right.
For D1F we can solve it as follows:
Lemma:Consider a graph with arbitrary initial weights, and for each edge we can add $$$1$$$ to exactly one of its vertices, we can make the final weights different.
Construction:Start from the vertex with the smallest initial weight,and for each step,take an unpicked vertex with smallest initial weight,and for all the unassigned edges connected to it, add 1 to the other vertex. This works in $$$O(n+m)$$$ or $$$O((n+m)\log(n+m))$$$ with set.
For the original problem, we can just reduce it to the lemma by properly assigning values in each triangle. It is clear that we can achieve $$$(+4,+4,+4)$$$ and $$$(+3,+4,+5)$$$ by only using weights $$$1,2,3$$$,and this are enough to handle all the cases if we add $$$(3,3,3)$$$ to each triangle initially and use the lemma.
Submission:201599238.
for div2B did anyone have any other explanation? the editorial seems very involved for a div2B :O
We just put odd numbers in 1st row and even in other or vice versa. To maximise the answer we shud take the first and second maximum and put in the first row first element and 2nd row last element and greedily add the remaining elements. U can refer my submission below
https://codeforces.com/contest/1816/submission/201541528
thank you for the reply,
I was able to make some random stuff during the round to get AC, but I was scared coz I can't prove that my solution is the best. which makes me less confident to submit during contests.
and that is why I felt this is hard for div2B
Yeah even I took 20 min to figure out. I just randomly took cases for n=4,6 and figured out. Eventually it worked. Greedy solutions will be tough to prove sometimes. But yeah we hv to try grinding it out
when will we have delta for div2, I cant wait to be cyan for the first time :v
For problem D2B, we intended to make a task about parity (the checkered property). However, we noticed that many participants discovered the solution by looking at samples and "proved by AC". In fact, the proof of this solution is very hard considering its position. Sorry if this task wasn't enjoyable for you.
We added some insights on finding the optimal construction in the editorial and made some minor fixes; sorry for the confusion. Still, I hope you had fun participating in the round :)
Div1B is a bad problem.
As Rating of Div 1 is already updated but why there is delay in Div 2 rating update?
Can anyone help me with a testcase where my code-201678387 for problem -C will fail?
The output should be
YES.The harder version of D2D/D1B can be also solved by optimizing the editorial solution:)
It's sufficient to notice that distances from 1 to vertices to the left of 1 on the "chain" are pairwise different and form a contiguous segment [1, x] for some x (we assume that segment is empty when 1 is a leaf). Similar thing happens for vertices to the right of 1 (segment [1, y]). So for distances d, such that $$$1\leq d \leq min(x, y)$$$ there are two indices corresponding to that distance. We can iterate over the distances (first decreasing, later increasing) and maintain previous vertex on chain. Every time when there are two possible next vertices on path, we can simply ask a question whether previous and next candidate are directly connected (distance between them is 1). And since $$$x+y=n-1$$$, we know that $$$min(x, y) \leq \frac{n}{2}$$$ and achieve the desired amount of questions.
My accepted code: 201628377
The interactor of problem D(div2)/B(div1) can be made TLE. Select a case that n>800,add O(n) random x between n/2 and 3n/2, and query n random pairs of nodes.As there are O(n^2) edges in the graph, it takes O(n^3) time for the interactor to answer all the query.
Submission:https://codeforces.com/contest/1815/submission/201700734
I thought there was some genius algorithm to update the distances for each query
Unfortunately, no, it is just a simple BFS (I don't know any genius algorithm to update the distances). So indeed the interactor can be made TLE. However, as far as I know, all the correct solutions only use $$$O(1)$$$ type 1 queries, so this issue shouldn't prevent any correct solutions from getting accepted.
Why is the interactor in D1B space intolerant. I spent almost an hour upsolving this problem just because of that :(
I think it is because you outputted extra debug lines?
Yeah, I guess, thanks
C. Between
Some test cases that I got wrong while upsolving:
The div is unrated?
idk my rating isnt changed
UP
culver0412 Just found this Easter Egg!
can some one help me, why my solution 201888165 is giving i = -1 for the output? problem : 1815B - Sum Graph
What I see is you didn't input $$$1$$$ or $$$-2$$$ after outputting the answer.
I did not get solution at first after reading editorial but solved Div2C using following method.
As per Question there are two operations for any array
a1 a2 a3 a4 ...i.e.aiandai+1aiandai+1I define two more operation using above 2 i.e.
ai+1 andai+2-1 ( using first operation onaiandai+1then second operation onai+1andai+2) orai-1 andai+2+1 ( using second operation onaiandai+1then first operation onai+1andai+2)Now back to our Problem :-
Consider Odd Case first
a1 a2 a3 a4 a5we can see that
a1,a3anda5can share any number among themselves( How ? by using self defined operation
ai-1 andai+2+1 and so on )similarly
a2anda4can share any their value among themselvesso we can assume there are two groups that can share their values, one group on even indexes and other on odd.
If we try to use operation 1 or 2 present in problem (
+1 to ai and ai+1or-1 from ai and ai+1) values will be added in or substracted from both groups so we neither gain or loose values so it can't help us if sequence is not sorted.But we notice one thing if we can take as many value from first index ( odd group ) and distribute it in center and give largest values to right most element which will make array sorted no matter what is even group.
Consider Even Case Now
a1 a2 a3 a4 a5 a6we can see thata1,a3anda5can share any number among themselves ( How ? by using self defined operationai-1 andai+2+1 and so on )similarly
a2,a4anda6can share any their value among themselves there are two groups again that can share their values, one group on even indexes and other on odd.If we try to use operation 1 or 2 present in problem (
+1 to ai and ai+1or-1 from ai and ai+1) values will be added in or substracted from both groups so we neither gain or loose values so it can't help us if sequence is not sorted.Unlike previous case, here we don't have option that we used earlier ( take from left most index as many as we like , distribute need values it in center and give largest to right most index ).
Here we can't arbitrarily take values from first index so what can we do really ?
These are still groups so we can use it for sorting. share values among even groups and odd groups as well.
Now consider two example:-
2 1 4 3
Odd group values ( odd index values ) :- 2 4
Even group values ( even index values ) :- 1 3
in this case no matter what even group share it can't beat last index value i.e. if we do this
0 6 ( shared values to right most index )
0 4 ( shard values to right most index )
we cant make it sorted ever.
So we Got our condition for even case
Even group total >= Odd Group total( why not vice versa ? because right most element will always belong to Even group. and for every odd groupaithere need high or equalai+1to make it sorted )Anyone can tell me why my solution for Div1B/Div2D gives the wrong answer on OJ? Also, is there any way to find the code for the interactor for such problems?
Checker comment:
wrong answer Printed answer is not a permutation :( (test case 1)That means your code reported an answer that's not a permutation. Please take a look at your solution and see what has to be changed. If you have any doubts, you can read the tutorial.
Also, there is no way to find the code for the interactor, unless the authors want to make it public for some reasons.
I think the note for 1815F - OH NO1 (-2-3-4) has a wrong explanation for the first test case. According to the problem statement, the weights should be added to (1, 2), (2, 3) and (3, 1) respectively, making the final weights [5, 3, 4, 0].
https://codeforces.com/problemset/status?my=on why this code not working,I am unable to figure out after many WA attempts for Div.1 B
This is a high-quality contest!
Im just curious, how do you solve the minimum number of jumps problem for Div2A?
Seems like your official solution on div1 D got an TLE on test #94. I figured out that the problem is you haven't clear the two maps before each subtask XD.
I submitted the same code that you submitted, but using C++ 20, and got accepted in 717ms
I think there is issues on C++ 14?
Maybe I would stop using C++ 14 ...
Initializing the Grid:
Begin by setting up a 2D grid. Initially, assign values to specific positions within this grid:
a[0][1] is initialized as 2 * n a[1][n] is set to (2 * n) — 1 Filling the Grid:
Set cur = 1.
Iterate from 0 to n — 1:
Populate the grid in an alternating pattern across rows using the formula a[i % 2][i] = cur, incrementing cur by 1 after each assignment. Reset cur to (2 * n) — 2.
Iterate from 3 to n in steps of 2:
Fill the grid in an alternating column pattern: Set a[0][i] = cur Set a[1][i — 1] = cur — 1 Decrease cur by 2 after each assignment. Printing the Grid:
Visualize the resulting grid after following these instructions, showcasing the unique pattern formed based on the initializations and iterations explained above.