We hope you enjoyed our problems :) We're working on editorials now, other problems will be added as soon as possible =)
In this problem one need to check whether it's possible to choose k elements from array A and m elements from array B so that each of chosen element in A is less than each of chosen elements in B. If it's possible then it's possible to choose k smallest elements in A and m largest elements in B. That means that in particular, k-th smallest element of A is less than m-th largest element in B. So, if A[k] < B[n - m + 1] then the answer is "YES" and if not, then the answer is "NO".
Problem author: zeliboba.
Problem developers: riadwaw, Kostroma.
Coming soon.
Let's count the number of ways to form a triple which can't represent triangle sides, and then we subtract this value from 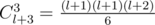 — the total number of ways to increase the sticks not more than l in total. This number is obtained from partition of l into 4 summands (la + lb + lc + unusedl = l), or can be counted using a
— the total number of ways to increase the sticks not more than l in total. This number is obtained from partition of l into 4 summands (la + lb + lc + unusedl = l), or can be counted using a for loop.
Now we consider triples a + la, b + lb, c + lc, where la + lb + lc ≤ l, la, lb, lc ≥ 0. Fix the maximal side, for example it would be a + la. We'll have to do the following algo for b + lb and c + lc in the same way. The triple is not a triangle with maximal side a + la if a + la ≥ b + lb + c + lc. If we iterate over la between 0 and l, we have the following conditions on lb, lc:
lb, lc ≥ 0. So, non-negative integers lb, lc should be such that lb + lc ≤ min(a - b - c + la, l - la). If we denote this minimum as x than we can choose lb, lc in 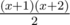 different ways (again we divide x into three summands: lb, lc and some unused volume). Also when we fix lb, there are x - lb + 1 ways to choose lc, so the overall number of pair lb, lc is
different ways (again we divide x into three summands: lb, lc and some unused volume). Also when we fix lb, there are x - lb + 1 ways to choose lc, so the overall number of pair lb, lc is
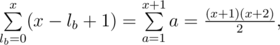
so we obtain the same formula.
To sum up, we need to iterate over the maximal side and over the addition to that side, then write these formulas, and subtract the result from the total number of different additions to the sides. The complexity of the solution is O(l).
Problem author: Kostroma.
Problem developers: Kostroma, riadwaw.
We can divide all indices [1;n] into groups by their remainder modulo k. While counting 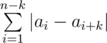 , we can consider each group separately and sum the distances between neighbouring numbers in each group.
, we can consider each group separately and sum the distances between neighbouring numbers in each group.
Consider one group, corresponding to some remainder i modulo k, i.e. containing aj for 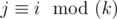 . Let's write down its numbers from left to right: b1, b2, ..., bm. Then this group adds to the overall sum the value
. Let's write down its numbers from left to right: b1, b2, ..., bm. Then this group adds to the overall sum the value
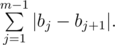
We can notice that if we sort b1, ..., bm in non-decreasing order, this sum will not increase. So, in the optimal answer we can consider that numbers in each group don't decrease. Furthermore, in that case this sum is equal to |bm - b1|.
Now consider two groups b1, ..., bm and c1, c2, ..., cl, both sorted in non-decreasing order. We claim that either b1 ≥ cl or bm ≤ c1, i.e. segments [b1, bm] and [c1, cl] can have common points only in their endpoints.
Why is this true? These groups add |bm - b1| + |cl - c1| to the overall sum. We consider the case c1 ≥ b1, the other is symmetric. If c1 < bm, then swapping c1 and bm will not increase the values these groups add to the answer, since the right border of b group moves to the left, and the left border of c group moves to the right. So, c1 ≥ bm in that case, and the assertion is proved.
Now we know that the values in each group should from a continuous segment of the sorted original array. In fact, we have 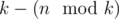 groups of size
groups of size 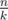 (so called small groups) and
(so called small groups) and 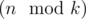 groups of size
groups of size 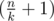 (so called large groups). Consider the following dynamic programming: dp[L][S] — the minimal sum of values added to the answer by L large groups and S small groups, if we choose the elements for them from the first
(so called large groups). Consider the following dynamic programming: dp[L][S] — the minimal sum of values added to the answer by L large groups and S small groups, if we choose the elements for them from the first 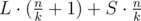 elements of the sorted array A. There are no more than O(k2) states, and each transition can be made in O(1): we choose large or small group to add and obtain the number it adds to the sum by subtracting two elements of the sorted array. The answer for the problem will be in
elements of the sorted array A. There are no more than O(k2) states, and each transition can be made in O(1): we choose large or small group to add and obtain the number it adds to the sum by subtracting two elements of the sorted array. The answer for the problem will be in 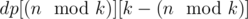 .
.
The overall complexity of the solution is 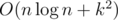 . We can note that in pretests
. We can note that in pretests 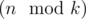 was quite small, and some slower solutions could pass, but they failed on final tests.
was quite small, and some slower solutions could pass, but they failed on final tests.
Problem author: zeliboba.
Problem developers: Kostroma, riadwaw.
Firstly let's assign values to variables occurring in our fomula only with negation or only without negation. After that we can throw away the disjuncts which contained them, since they are already true, and continue the process until it is possible. To make it run in time limit, one should use dfs or bfs algorithm to eliminate these variables and disjuncts.
So now we have only variables which have both types of occurrences in disjucnts. Let's build a graph with the vertices corresponding to disjuncts, and for each varible a make an edge between the disjuncts that contain a and !a. Now we should choose the directions of edges in this graph in such a way that every vertex has at least one incoming edge.
We can notice that if some connected component of this graph is a tree, the solution is not possible: on each step we can take some leaf of this tree, and we have to orient its only edge to it, and then erase the leaf. In the end we'll have only one vertex, and it'll not have any incoming edges.
Otherwise, take some cycle in the component and orient the edges between neighbouring vertices along it. Then run dfs from every vertex of the cycle and orient each visited edge in the direction we went along it. It is easy to easy that after this process every vertex will have at least one incoming edge.
So, we should consider cases with the variables which values can be assigned at once, than construct a graph from disjuncts and variables and find whether each connected component has a cycle. If so, we also should carefully construct the answer, assigning the remaining variables their values, looking at the directions of the edges in the graph. The overall complexity is O(n + m).
Problem author: zeliboba.
Problem developers: Kostroma, zeliboba, yarrr.
Coming tomorrow :)
571E - Геометрические прогрессии
Coming soon.






