I like the idea of Endagorion to supplement the problems analysis with small challenges, somehow related to the problem preparation, it's generalization, or more effective solution. Following this, some problems in this analysis are also complemented with this sort of tasks.
Div. 2A (Wizards' Duel)
Idea of the problem: Roman Gusarev, development: timgaripov.
Let's start with determining the position of the first collision. Two impulses converge with a speed p + q, so the first collision will occur after 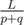 seconds. The coordinate of this collision is given by the formula
seconds. The coordinate of this collision is given by the formula 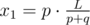 .
.
Note, that the distance one impulse passes while returning to it's caster is equal to the distance it has passed from the caster to the first collision. That means impulses will reach their casters simultaneously, and the situation will be identic to the beginning of the duel. Hence, the second collision (third, fourth, etc) will occur at exactly the same place as the first one.
Code example: 13836780.
Div. 2B (Rebranding)
Idea of the problem: glebushka98, development: thefacetakt.
Trivial solution will just emulate the work of all designers, every time considering all characters of the string one by one and replacing all xi with yi and vice versa. This will work in O(n·m) and get TL.
First one should note that same characters always end as a same characters, meaning the position of the letter doesn't affect the result in any way. One should only remember the mapping for all distinct characters. Let p(i, c) be the mapping of c after i designers already finished their job. Now:
- p(0, c) = c
- If p(i - 1, c) = xi, then p(i, c) = yi
- Same, if p(i - 1, c) = yi, then p(i, c) = xi
This solution complexity is O(|Σ|·m + n) and is enough to pass all the tests.
Challenge: improve the complexity to O(Σ + n + m).
Code examples: 13837577 implements O(|Σ|·m + n) and 13839154 stands for O(|Σ| + n + m).
Div. 2C\Div. 1A (Median Smoothing)
Problem idea and development: Sender.
We will call the element of a sequence stable, if it doesn't change after applying the algorithm of median smoothing for any number of times. Both ends are stable by the definition of the median smoothing. Also, it is easy to notice, that two equal consecutive elements are both stable.
Now we should take a look at how do stable elements affect their neighbors. Suppose ai - 1 = ai, meaning i - 1 and i are stable. Additionaly assume, that ai + 1 is not a stable element, hence ai + 1 ≠ ai and ai + 1 ≠ ai + 2. Keeping in mind that only 0 and 1 values are possible, we conclude that ai = ai + 2 and applying a median smoothing algorithm to this sequence will result in ai = ai + 1. That means, if there is a stable element in position i, both i + 1 and i - 1 are guaranteed to be stable after one application of median smoothing. Now we can conclude, that all sequences will turn to stable at some point.
Note, that if there are two stable elements i and j with no other stable elements located between them, the sequence of elements between them is alternating, i.e. ak = (ai + k - i)mod2, where 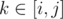 . One can check, that stable elements may occur only at the ends of the alternating sequence, meaning the sequence will remain alternating until it will be killed by effect spreading from ending stable elements.
. One can check, that stable elements may occur only at the ends of the alternating sequence, meaning the sequence will remain alternating until it will be killed by effect spreading from ending stable elements.
The solution is: calculate max(min(|i - sj|)), where sj are the initial stable elements. Time complexity is O(n).
Challenge 1: hack the solution that just applies median smoothing until something changes.
Challenge 2: think of how to speed up the algorithm from challenge 1 using bitmasks (still gets TL).
Code examples: 13838940 and 13838480.
Div. 2D\Div. 1B (Chip 'n Dale Rescue Rangers)
Problem idea and development: StopKran.
If the velocity of the dirigible relative to the air is given by the vector (ax, ay), while the velocity of the wind is (bx, by), the resulting velocity of the dirigible relative to the plane is (ax + bx, ay + by).
The main idea here is that the answer function is monotonous. If the dirigible is able to reach to target in  seconds, then it can do so in
seconds, then it can do so in 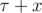 seconds, for any x ≥ 0. That is an obvious consequence from the fact the maximum self speed of the dirigible is strictly greater then the speed of the wind at any moment of time.
seconds, for any x ≥ 0. That is an obvious consequence from the fact the maximum self speed of the dirigible is strictly greater then the speed of the wind at any moment of time.
For any monotonous function we can use binary search. Now we only need to check, if for some given value  it's possible for the dirigible to reach the target in
it's possible for the dirigible to reach the target in  seconds. Let's separate the movement of the air and the movement of the dirigible in the air. The movement cause by the air is:
seconds. Let's separate the movement of the air and the movement of the dirigible in the air. The movement cause by the air is:
- (xn, yn) =
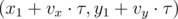 , if
, if 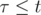 ;
; - (xn, yn) =
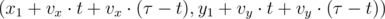 , for
, for 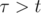 .
.
The only thing we need to check now is that the distance between the point (xn, yn) and the target coordinates (x2, y2) can be covered moving with the speed vmax in  seconds assuming there is no wind.
seconds assuming there is no wind.
Time complexity is 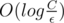 , where C stands for the maximum coordinate, аnd ε — desired accuracy.
, where C stands for the maximum coordinate, аnd ε — desired accuracy.
Challenge 1: think of the solution in case it's not guaranteed that the dirigible is faster than the wind.
Challenge 2: can you come up with O(1) solution?
Code examples: 13838659 and 13842505.
Div. 2E\Div. 1C (Three States)
Problem idea and development: haku.
Affirmation. Suppose we are given an undirected unweighted connected graph and three distinct chosen vertices u, v, w of this graph. We state that at least one minimum connecting network for these three vertices has the following form: some vertex c is chosen and the resulting network is obtained as a union of shortest paths from c to each of the chosen vertices.
Proof. One of the optimal subgraphs connecting these three vertices is always a tree. Really, we can take any connecting subgraph and while there are cycles remaining in it, take any cycle and throw away any edge of this cycle. Moreover, only vertices u, v and w are allowed to be leaves of this tree, as we can delete from the network any other leaves and the network will still be connected. If the tree has no more than three leaves, it has no more than one vertex with the degree greater than 2. This vertex is c from the statement above. Any path from c to the leaves may obviously be replaced with the shortest path. Special case is than there is no node with the degree greater than 2, meaning one of u, v or w lies on the shortest path connecting two other vertices.
The solution is: find the shortest path from each of the chosen vertices to all other vertices, and then try every vertex of the graph as c. Time complexity is O(|V| + |E|).
To apply this solution to the given problem we should first build a graph, where cells of the table stand for the vertices and two vertices are connected by an edge, if the corresponding cells were neighboring. Now we should merge all vertices of a single state in one in order to obtain a task described in the beginning. Time complexity is a linear function of the size of the table 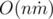 .
.
Code examples: 13843265 — the solution described above that uses 0-1 bfs instead of merging, 13840329 — another approach that tries to different cases.
Div. 1D (Top Secret Task)
Problem idea and development: glebushka98.
If 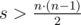 , than the sum of k minimums is obviously an answer.
, than the sum of k minimums is obviously an answer.
Let i1 < i2 < ... < ik be the indices of the elements that will form the answer. Note, that the relative order of the chosen subset will remain the same, as there is no reason to swap two elements that will both be included in the answer. The minimum number of operations required to place this k elements at the beginning is equal to 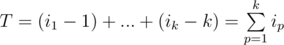 —
— 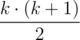 .
.
T ≤ S 
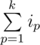 ≤
≤ 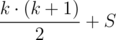 .
. 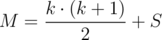 .
.
Calculate the dynamic programming d[i][j][p] &mdash minimum possible sum, if we chose j elements among first i with the total indices sum no greater than p. In order to optimize the memory consumption we will keep in memory only two latest layers of the dp.
Time complexity is O(n4), with O(n3) memory consumption.
Code examples: 13845513 and 13845571.
Div. 1E (Birthday)
Problem idea: meshanya, development: romanandreev.
The given problem actually consists of two separate problems: build the directed graph of substrings relation and find the maximum Задача естественно разбивается на две подзадачи: быстрое построение графа вложенности и нахождение максимального независимого множества в этом графе. Заметим сразу, что если строка s2 является подстрокой строки s1, а строка s3 является подстрокой строки s2, то s3 очевидно является подстрокой строки s1. Таким образом, граф вложений зададаёт частично упорядоченное множество.
Для быстрого построения графа воспользуемся алгоритмом Ахо-Корасик. С помощью данной структуры мы построим все существенные рёбра графа, то есть такие рёбра  , что не найдётся w, такого что
, что не найдётся w, такого что  и
и  . Одним из возможных способов является:
. Одним из возможных способов является:
- Построить структуру Ахо-Корасик;
- Для каждой вершины найти и запомнить ближайшую терминальную в суффиксном пути;
- Ещё раз скормить каждую строку автомату Ахо-Корасик, при этом каждый раз после добавления очередного символа требуется проводить ребро в ближайшую терминальную вершину в суффиксном пути;
- Кроме существенных рёбер, данный алгоритм возможно добавит ещё какие-то корректные рёбра, но это никак не влияет на результат работы следующего шага;
- Транзитивно замкнуть построенный граф.
Для решение второй части данной задачи требует применить теорему Дилворта. Восстановление ответа следует из конструктивного доказательства теоремы.
Получаем O(L + n3) на построение графа + O(n3) на нахождение максимальной антицепи, итоговая сложность решения: O(L + n3), где L — суммарная длина всех строк.
Поздравляем ikatanic — единственного человека сдавшего эту задачу во время тура. Для дальнейшего уточнения решения предлагается посмотреть 13851141.
Упражнение: научитесь решать задачу с сохранением асимптотики, при условии что требуется найти множество строк максимальное не по размеру, а по суммарной длине.






