I'm terribly sorry for the delay.
Please report any mistakes.
Author: Tigutor
You had to print all numbers of form kx for non-negative integers x that lie with the range [l;r]. A simple cycle works: start with 1 = k0, go over all powers that do not exceed r and print those which are at least l. One should be careful with 64-bit integer overflows: consider the test l = 1, r = 1018, k = 109, the powers will be 1, 109, 1018, and the next power is 1027, which does not fit in a standard integer type.
Author, developer: ch_egor
You were asked to print the product of n large numbers, but it was guaranteed that at least n - 1 are beautiful. It's not hard to see that beautiful numbers are 0 and all powers of 10 (that is, 1 followed by arbitrary number of zeros). If there is at least one zero among the given numbers, the product is 0. Otherwise, consider the only non-beautiful number x (if all numbers are beautiful, consider x = 1). Multiplying x by 10t appends t zeros to its decimal representation, so in this case we have to find the only non-beautiful number and print it with several additional zeros.
We tried to cut off all naive solutions that use built-in long numbers multiplication in Python or Java. However, with some additional tricks (e.g., ``divide-and-conquer'') this could pass all tests.
Author, developer: platypus179
Consider distances between the point P and all points of the polygon. Let R be the largest among all distances, and r be the smallest among all distances. The swept area is then a ring between circles of radii R and r, and the answer is equal to π (R2 - r2).
Clearly, R is the largest distance between P and vertices of the polygon. However, r can be the distance between P and some point lying on the side of the polygon, therefore, r is the smallest distance between P and all sides of the polygon.
To find the shortest distance between a point p and a segment s, consider a straight line l containing the segment s. Clearly, the shortest distance between p and l is the length of the perpendicular segment. One should consider two cases: when the end of the perpendicular segment lies on the segment s (then the answer is the length of the perpendicular segment), or when it lies out of s (then the answer is the shortest distance to the ends of s).
Author: cdkrot
Developers: cdkrot, galilei2000, ch_egor
Let's save the original positions of skills and then sort the skills in non-increasing order (almost decreasing) by current level. We can always restore original order after.
Imagine that we have decided that we want to use the minimum level X and now we're choosing which skills we should bring to the maximum.
At first, let's rise all skills below X to level X, this will set some tail of array to X. But the original array was sorted, and this new change will not break the sort! So our array is still sorted.
Obviously, the skills we want to take to the maximum are the ones with highest current level. They are in the prefix of array. It is easy to show that any other selection is no better than this greedy one.
Now we have shown that the optimal strategy is to max out the skills in some prefix. Now let's solve the problem.
Let's iterate over prefix to max out, now on each iteration we need to know the highest minimum we can achieve, let's store the index of the first element outside the prefix such that it is possible to reach the minimum level ≥ arrindex.
It is easy to recalc this index, it slightly moves forward each turn and, after precalcing the sum of all array's tails, you can update it easily (just move it forward until the invariant above holds). And knowing this index is enough to calc the current highest possible minimum level (min(A, arrindex + ⌊ sparemoney / (n - index)⌋).
How to restore the answer? Actually, all you need to know is the count of maximums to take and minimum level to reach.
Author: cdkrot
Developers: cdkrot, crossopt, ch_egor
Surprisingly, the nice cuts can't be put randomly. Let's take a look on the first picture above (red lines represent nice cut points). But since the necklace is symmetrical relative to nice cuts, the cut points are also symmetrical relative to nice cuts, so there is one more cut (see picture two). Repeating this process, we will split the whole necklace into parts of the same size (picture three).


If the number of parts is even, then each part can be taken arbitrarily, but the neighbouring parts must be reverses of each other (e.g. "abc" and "cba"). This is an implication of the cuts being nice.
If the number of parts is odd, then each part is equal to each other and is a palindrome, this is an implication of the cuts being nice too.
Anyway, the number of characters in each part is equal, so amount of parts can't be greater than 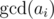 . Actually, it may be zero,
. Actually, it may be zero, 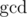 or its divisor.
or its divisor.
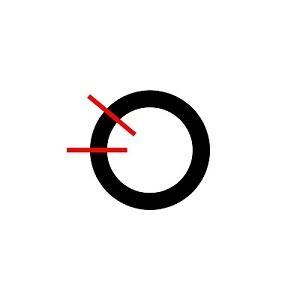
If the number of odd-sized colors is zero, then the sum is even and gcd is even, this way we can construct a building block containing exactly
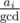 beads of i-th color, (gcd being gcd of all counts), then build beads of gcd parts, where each part equal to building block, with neighbouring parts being reverses. Since gcd is even, everything is ok.
beads of i-th color, (gcd being gcd of all counts), then build beads of gcd parts, where each part equal to building block, with neighbouring parts being reverses. Since gcd is even, everything is ok.If the number of odd-sized colors is one, then the sum is odd and gcd is odd. Building block have to be built as a palindrome containing
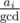 beads of i-th color, exactly n - 1 of colors will be even and one odd, put the odd one in center, others on sides (aabcbaa). Everything is ok.
beads of i-th color, exactly n - 1 of colors will be even and one odd, put the odd one in center, others on sides (aabcbaa). Everything is ok.If num of odd counts is geq2. Gcd is odd, all its divisors too, so our building block has to be palindrome. Let k denote the number of parts. A building block will contain
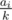 beads of color i, at least two of these numbers are odd, it is impossible to build such a palindrome. The answer is zero.
beads of color i, at least two of these numbers are odd, it is impossible to build such a palindrome. The answer is zero.
Complexity: O(sum), just to output answer.
Bonus. How to solve problem, if you are allowed to discard any subset of beads before constructing necklace?
Bonus. Given a necklace scheme (like one you were asked to output), how to determine number of nice cuts, O(sum), no suffix structures or hashes?
Authors: ch_egor and others
Developer: cdkrot
Obviously, the answer is -1 iff two important cities are adjacent.
If there was a single query, can we answer it in O(n) time? Let's choose a root arbitrarily. We can note there is an optimal answer that erases two types of vertices: vertices that lie on a vertical path between two important vertices, or LCA of some pair of important vertices.
Let's do a subtree DP that counts the answer for the subtree of v, as well as if there is any important vertex still connected to v in the answer. How do we count it? If v is important, then we should disconnect it from any still-connected vertices from below by erasing these children which contain them. If v is not important, then we erase it iff there are more than one still-connected important vertices below. All calculations are straightforward here.
How do we process many queries now? There are many possible approaches here (for reference, look at the accepted solutions). The author's solution was as follows: if we have a query with k important vertices, then we can actually build an auxiliary tree with O(k) vertices and apply the linear DP solution to it with minor modifications.
How to construct the auxiliary tree? We should remember the observation about LCAs. Before we start, let us DFS the initial tree and store the preorder of the tree (also known as "sort by tin"-order). A classical exercise: to generate all possible LCAs of all pairs among a subset of vertices, it suffices to consider LCAs of consecutive vertices in the preorder. After we find all the LCAs, it is fairly easy to construct the tree in O(k) time. Finally, apply the DP to the auxiliary tree. Note that important cities adjacent in the auxiliary tree are actually not adjacent (since we've handled that case before), so it is possible to disconnect them.
If we use the standard "binary shifts" approach to LCA, we answer the query in 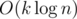 time, for a total complexity of
time, for a total complexity of  .
.
Author, developer: Endagorion
The key observation: any way to cross out the word w looks roughly as follows:
..v<1.>>v.2<...
..>>>>^.>>>^...
That is, there can be following parts:
go back a symbols in one row, then go forward a symbols in the other row (possibly a = 0)
go forward with arbitrarily up and down shifts in a snake-like manner
go forward b symbols in one row, then go back b in the other row (possibly b = 0)
Note that the "forward" direction can be either to the left or to the right. It is convenient that for almost any such way we can determine the "direction" as well as the places where different "parts" of the path (according to the above) start. To avoid ambiguity, we will forbid a = 1 or b = 1 (since such parts can be included into the "snake").
Fix the direction. We will count the DP dx, y, k for the number of ways to cross out first k letters of w and finished at the cell (x, y) while being inside the snake part of the way. The transitions are fairly clear (since the snake part only moves forward). However, we have to manually handle the first and the last part. For each cell and each value of k we can determine if the "go-back-then-go-forward" maneuver with parameter k can be performed with the chosen cell as finish; this can be reduced to comparing of some substrings of field of rows and the word w (and its reversed copy). In a similar way, for any state we can check if we can append the final "go-forward-then-go-back" part of the path to finally obtain a full-fledged path.
This DP has O(n2) states and transitions. However, there are still some questions left. How do we perform the substring comparisons? There is a whole arsenal of possible options: (carefully implemented) hashes, suffix structures, etc. Probably the simplest way is to use Z-function for a solution that does O(n2) precalc and answers each substring query in O(1) time (can you see how to do it?).
Also, there are paths that we can consider more than once. More precisely, a path that consists only of the "go-forward-the-go-back" part will be counted twice (for both directions), thus we have to subtract such paths explicitly. Every other path is counted only once, thus we are done. (Note: this does not exactly work when w is short, say, 4 symbols or less. The simplest way is to implement straightforward brute-force for such cases.)






