This is an article on how to compute the chromatic number of a graph effectively.
The original article was written in Japanese here.
http://www.learning-algorithms.com/entry/2018/01/27/235959
What is "chromatic number?"
Chromatic number is the minimum number of colors to color all the vertices, so that no two adjacent vertices have the same color.
If you look at a tree, for instance, you can obviously color it in two colors, but not in one color, which means a tree has the chromatic number 2.
Chromatic polynomial
In order to discuss the chromatic number, I introduce the chromatic polynomial first.
The chromatic polynomial P(K), is the number of ways to color a graph within K colors. Let's take a tree with n ( ≥ 2) vertices as an example. First of all, a tree has at least one leaf, so color it first with any color. After that, you can just color the rest with a different color from a previous color in order. This concludes the following chromatic polynomial for a tree.
P(K) = K(K - 1)n - 1 ... (1)
Now, we are ready to calculate the chromatic number.
Compute the chromatic number
Chromatic number is computed in the following way:
- Find the chromatic polynomial P(K)
- Evaluate the polynomial in the ascending order, K = 1, 2, ..., n
- When the value gets larger than 0 for the first time, the value of K is the chromatic number
Let's compute the chromatic number of a tree again now. Using (1), we can tell P(1) = 0, P(2) = 2 > 0 , and thus the chromatic number of a tree is 2.
I describe below how to compute the chromatic number of any given simple graph.
As I mentioned above, we need to know the chromatic polynomial first. If you can divide all the vertices into K independent sets, you can color them in K colors because no two adjacent vertices share the edge in an independent set.
Let V be the set of vertices of a graph. For any subsets 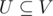 , let me define ind(U) as 'the number of subsets of U, which compose an independent set.'
, let me define ind(U) as 'the number of subsets of U, which compose an independent set.'
The number of ways to choose K sets from ind(U) is ind(U)K, therefore, Inclusion-exclusion principle allows you to calculate the chromatic number in the following way:
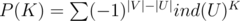
The implementation is really simple. ind(U) can be calculated by bitDP.
The time complexity is O(2n n).
int ChromaticNumber(const vector<int> &g) {
int n = g.size();
if (n == 0) return 0;
//randomly choose a large prime
const int modulo = 1077563119;
int all = 1 << n;
vector<int> ind(all), s(all);
for (int i = 0; i < all; i ++) s[i] = ((n - __builtin_popcount(i)) & 1 ? -1 : 1);
ind[0] = 1;
for (int i = 1; i < all; i ++) {
int ctz = __builtin_ctz(i);
ind[i] = ind[i - (1 << ctz)] + ind[(i - (1 << ctz)) & ~g[ctz]];
if (ind[i] >= modulo) ind[i] -= modulo;
}
//compute the chromatic number (= \sum (-1)^{n - |i|} * ind(i)^k)
for (int k = 1; k < n; k ++) {
long long sum = 0;
for (int i = 0; i < all; i ++) {
long long cur = ((s[i] * (long long) ind[i]) % modulo);
s[i] = cur;
sum += cur;
}
if (sum % modulo != 0) return k;
}
return n;
}
That's it! Thank you for reading.






