1575A. Another Sorting Problem
Author: hocky
Developer: richiesenlia
Editorialist: hocky
Observe that the even-indexed character of the string can be transformed from A-Z to Z-A. E.g. for the first example:
- AA → AZ
- AB → AY
- BB → BY
- BA → BZ
- AZ → AA
Now, you can use any known algorithms to sort the string as usual. You can sort it in linear time with trie, or std::sort in $$$O(nm \log n)$$$ time.
Time Complexity : $$$O(nm)$$$ or $$$O(nm \log n)$$$
1575B. Building an Amusement Park
Author: Panji
Developer: hocky, rama_pang
Editorialist: hocky, rama_pang
We can binary search the answer $$$r$$$ in this case. Here, bird's habitats are referred as points. First of all, define a function $$$c(x)$$$ as the maximum number of points that can be covered with a circle of radius $$$x$$$ through the origin.
Define the park as a circle with radius $$$x$$$ and $$$\theta$$$, in a polar coordinate representation. Observe that each points have a radial/angle segment of which the point $$$p_i$$$ will be inside the circle if and only if $$$\theta$$$ belongs to the radial segment of $$$[L_{p_{i}}, R_{p_{i}}]$$$, where $$$-\pi < L_{p_{i}}, R_{p_{i}} \leq \pi$$$.
E.g for $$$x = 4$$$, Observe the $$$L_{p_{3}}$$$ for the $$$p_3 = (1, 5)$$$.
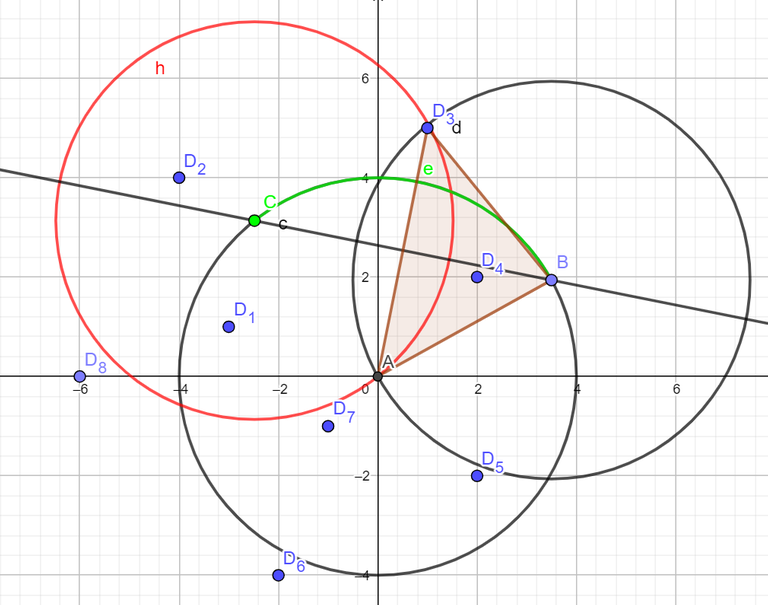
The green radial segment $$$e$$$ represents the $$$[L_{p_{3}}, R_{p_{3}}]$$$. Now, to find the two end points $$$B_i$$$ and $$$C_i$$$ of the arc for each point $$$p_i$$$. Because the triangle that is made by those 3 points are an isosceles triangle, simply find the angle where the distance of $$$p_i$$$ and $$$B_i$$$ equals to $$$x$$$, that is $$$\Delta = \cos^{-1}\dfrac{||p_i||}{2r}$$$. Now the segment can be found by calculating the angle of $$$\tan^{-1}p_i \pm \Delta$$$. Do a radial sweep to find the maximum number of points.
Time complexity is $$$O(n \log n \cdot \log(\text{MAX_R} \cdot \epsilon^{-1}))$$$.
We can optimize the binary search part further, since we only need $$$\log(\epsilon^{-1})$$$ most significant digits. We can binary search the position of the first non-zero digit in $$$O(\log\log(\text{MAX_R}))$$$, then use a normal binary search with $$$O(\log(\epsilon^{-1}))$$$ steps. In practice, this improves the time by around a factor of 2.
Time complexity: $$$O(n \log n \cdot \log(\text{MAX_R} \cdot \epsilon^{-1}))$$$ or $$$O(n \log n \cdot \log(\log(\text{MAX_R}) \cdot \epsilon^{-1}))$$$.
1575C. Cyclic Sum
Author: steven.novaryo
Developer: steven.novaryo
Editorialist: steven.novaryo
Let a valid segment $$$[l, r]$$$ be a segment in $$$b$$$ where the sum of elements in the segment is divisible by $$$k$$$.
We can try to solve a simpler problem: find the number of valid segments such that the right endpoint ends at $$$1$$$. That is, the valid segments $$$[l, 1]$$$ ($$$1 \leq l \leq n \cdot m$$$).
Let $$$prefix(p) = \sum_{i=1}^{p} {b[i]}$$$ and $$$cnt$$$ be an array where the $$$cnt[i]$$$ denote the number of $$$p$$$ ($$$1 \leq p \leq n \cdot m$$$) such that $$$i \equiv prefix(p) \mod k$$$.
Notice that the number of valid segment $$$[l, 1]$$$ is $$$cnt[prefix(n \cdot m) + b[1]]$$$. Furthermore, the number of valid segments $$$[l, 1 + x \cdot n]$$$ ($$$0 \leq x \leq m-1$$$) is the same as the number of valid segment $$$[l, 1]$$$.
Thus, we only need to calculate the number of valid segments for $$$[l, r]$$$ with $$$1 \leq l \leq n \cdot m$$$ and $$$1 \leq r \leq n$$$, then multiply the final result by $$$m$$$.
First we need to find the array $$$cnt$$$. Let $$$sum = prefix(n)$$$.
When $$$sum \equiv 0 \mod k$$$, we can find $$$cnt$$$ in a straightforward manner.
Now assume $$$sum \not\equiv 0 \mod k$$$. For a fixed $$$i$$$, let's try to find the contribution of $$$prefix(i + x \cdot n)$$$ for all $$$0 \leq x \leq m-1$$$ to $$$cnt$$$ at once. Observe that if one make a directed graph with $$$(i, \ (i + sum) \bmod k)$$$ for $$$0 \leq i < k$$$ as the edges, one will get a cycle of length $$$k$$$ (since $$$k$$$ is prime) as the result. To find the contribution of $$$prefix(i + x \cdot n)$$$, we can do a range add operation on this cycle. This can be done with offline prefix sums (prefix difference) in $$$O(k)$$$ total.
Now that we have the array $$$cnt$$$, we can find the number of valid segments that ends at $$$1$$$ easily. To find valid segment that ends at index $$$2$$$, we can modify $$$cnt$$$ by adding $$$prefix(n \cdot m) + b[1]$$$ to the counter and removing $$$b[1]$$$. We do this for all $$$1 \leq r \leq n$$$.
This solution is also applicable for arbitary $$$k$$$, albeit multiple cycles will be generated and must be handled separatedly.
Time complexity: $$$O(n + k)$$$
1575D. Divisible by Twenty-Five
Author: hocky
Developer: hocky
Editorialist: hocky
There are no dirty tricks to solve this problem. Brute force all possible number between $$$i \in [10^{|s| - 1}, 10^{|s|} - 1]$$$, with step $$$i := i + 25$$$. You might want to handle when $$$|s| = 1$$$, because $$$0$$$ is a valid $$$s$$$, if possible. For easier implementation, you can use the std::to_string(s) in C++.
It is also possible to solve it in $$$O(|s|)$$$ by case analysis.
Time complexity: $$$O(\frac{1}{25} \cdot |s| \cdot 10^{|s|})$$$ or $$$O(|s|)$$$.
#include <bits/stdc++.h>
using namespace std;
#define sz(x) (int)(x).size()
typedef long long LL;
LL expo(LL a, LL b){
// a %= MOD; // USE THIS WHEN N IS REALLY BIG!
LL ret = 1;
while(b > 0){
if(b&1) ret = (ret*a);
a = (a*a); b >>= 1;
}
return ret;
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
string s; cin >> s;
int low = expo(10, sz(s) - 1);
int high = expo(10, sz(s)) - 1;
if(low == 1) low--;
while(low%25) low++;
int ans = 0;
for(;low <= high;low += 25){
string current = to_string(low);
char xval = '-';
bool can = 1;
for(int i = 0;i < sz(s);i++){
if(s[i] == '_') continue;
if(s[i] == 'X'){
if(xval != '-' && xval != current[i]){
can = 0;
break;
}
xval = current[i];
}else if(s[i] != current[i]){
can = 0;
break;
}
}
ans += can;
}
cout << ans << endl;
}
1575E. Eye-Pleasing City Park Tour
Author: steven.novaryo
Developer: rama_pang, hocky, steven.novaryo
Editorialist: rama_pang, steven.novaryo
We can use centroid decomposition to solve this problem.
Suppose we find the centroid $$$cen$$$ of the tree, and root the tree at $$$cen$$$. We consider each subtree of the children of $$$cen$$$ as different groups of vertices. We want to find the sum of $$$f(u,v)$$$ for all valid tours, such that $$$u$$$ and $$$v$$$ are from different groups.
We can solve this with basic inclusion-exclusion. We count the sum of $$$f(u,v)$$$ where the path $$$u \to cen \to v$$$ uses less than $$$k$$$ tickets, without caring which group $$$u,v$$$ belongs to. Then, we can subtract it by only considering $$$u \to cen \to v$$$ where $$$u,v$$$ belongs from the same group.
Define $$$cost(u)$$$ as the number of tickets you need to go from $$$u$$$ to $$$cen$$$. For a fixed set of vertices $$$S$$$, you can count $$$f(u,v)$$$ where $$$cost(u) + cost(v) + z \leq k$$$ with prefix sums. Note that $$$z$$$ depends on whether the last edge of the path from $$$u \to cen$$$ and $$$v \to cen$$$ has different colors. We can do all of these in $$$O(|S|)$$$.
We use the solution above while setting $$$S$$$ as the set of all vertices in $$$cen$$$'s subtree, or the set of vertices with the same group.
Because the depth of a centroid tree is $$$O(\log n)$$$, the overall complexity of the solution is $$$O(n \log n)$$$.
1575F. Finding Expected Value
Author: rama_pang
Developer: rama_pang
Editorialist: rama_pang
We can use this trick, which is also explained below.
Suppose $$$a_i \neq -1$$$ for now. We want to find a function $$$F(a)$$$ such that $$$\mathbb{E}(F_{t + 1} - F_t | F_t) = -1$$$, where $$$F_t$$$ is the value of $$$F(a)$$$ at time $$$t$$$. If we can find such a function, then the expected stopping time is equal to $$$F(a_0) - F(a_T)$$$, where $$$a_0$$$ is the initial array before doing any operation, and $$$a_T$$$ is the final array where we don't do any more operation (that is, all elements of $$$a_T$$$ are equal).
Suppose $$$occ(x)$$$ is the number of occurrences of $$$x$$$ in the current array, for some $$$0 \leq x < k$$$. It turns out we can find such $$$F$$$ satisfying $$$F = \sum_{x = 0}^{k - 1} f(occ(x))$$$ for some function $$$f$$$. We now try to find $$$f$$$.
Suppose we currently have $$$a_t$$$, and we want to find the expected value of $$$F(a_{t + 1})$$$. There are two cases to consider:
- $$$\forall x, occ_{t + 1}(x) = occ_t(x)$$$ if $$$a_i$$$ doesn't change when doing the operation. This happens with probability $$$\frac{1}{k} \cdot \frac{occ_t(x)}{n}$$$ for each $$$x$$$.
- Otherwise, there exist some $$$x, y$$$ ($$$x \neq y$$$) such that $$$occ_{t + 1}(x) = occ_t(x) - 1$$$ and $$$occ_{t + 1}(y) = occ_t(y) + 1$$$. This happens if initially $$$a_i = x$$$, then by doing the operation we change it to $$$y$$$. This happens with probability $$$\frac{1}{k} \cdot \frac{occ_t(x)}{n}$$$ for each $$$x,y$$$.
Thus,
Suppose $$$a = occ_t(x)$$$. If we can find $$$f$$$ such that
then $$$f$$$ satisfies $$$F$$$.
So we can set $$$f$$$ to any function that satisfies the recursive formula above, and then derive $$$F$$$.
To handle $$$a_i = -1$$$, note that $$$F$$$ depends only on the occurrence of each value $$$x$$$ ($$$0 \leq x < k$$$), and each of them is independent. Therefore, we can count the contribution for each $$$x$$$ towards all possible final arrays separately. This is easy to do in $$$O(n)$$$.
Moreoever, there is only $$$O(\sqrt{n})$$$ values of $$$occ(x)$$$ in the initial array (before changing $$$a_i = -1$$$), and each $$$x$$$ with the same occurrences contribute the same amount. Therefore, we can solve the problem in $$$O(n \sqrt{n})$$$.
1575G. GCD Festival
Author: yz_
Developer: hocky, yz_
Editorialist: rama_pang
Define:
- $$$d(n)$$$ as the set of all divisors of $$$n$$$;
- $$$\phi(x)$$$ as the euler totient function of $$$x$$$; and
- $$$d(a, b)$$$ as the set of all divisors of both $$$a$$$ and $$$b$$$; or equivalently, $$$d(\gcd(a, b))$$$.
Observe that $$$\sum_{x \in d(n)}\phi(x) = n$$$. This implies $$$\sum_{x \in d(a, b)}\phi(x) = \gcd(a,b)$$$
If we only iterate $$$y$$$ where $$$y$$$ is a divisor of one of $$$a_{ix}$$$, we can compute the above summation in $$$O(n \log n \max_{i=1}^n(|d(a_i)|))$$$.
1575H. Holiday Wall Ornaments
Author: hocky
Developer: Sakamoto, hocky
Editorialist: hocky, rama_pang
Do a dynamic programming with three states:
- Position in $$$s$$$
- Position in $$$t$$$
- How many matches left.
define the dynamic programming of $$$dp[a][b][rem]$$$ as the minimum cost of having the string $$$p = s[1..a]$$$, $$$rem$$$ matches left, and the longest prefix match between $$$s$$$ and $$$t$$$ is at $$$b$$$. The answer will be at $$$dp[n][c][0]$$$ for any arbitrary $$$c$$$.
The transition can first be precomputed with brute force in $$$O(n^3)$$$ or with Aho-Corasick.
Time complexity: $$$O(n^3)$$$
Space complexity: $$$O(n^2)$$$
1575I. Illusions of the Desert
Author: JulianFernando
Developer: JulianFernando, hocky
Editorialist: hocky
Note that $$$\max(|a_x + a_y|, |a_x - a_y|) = |a_x| + |a_y|$$$.
Now the problem can be reduced to updating a vertex's value and querying the sum of values of vertices in a path.
This can be done in several ways. One can use euler tour tree flattening method, as described in Euler Tour Magic by brdy blog, or use heavy-light decomposition.
Time complexity : $$$O((q + n) \log^2 n)$$$ or $$$O((q + n) \log n)$$$
1575J. Jeopardy of Dropped Balls
Author: richiesenlia
Developer: richiesenlia
Editorialist: hocky
Naively simulating the ball's path is enough, and runs in $$$O(nm + nk)$$$. Note that if we visit a non-$$$2$$$ cell, then the path length of the current ball is increased by $$$1$$$, and then the cell turns into $$$2$$$. So the total length of all paths can be increased by at most $$$O(nm)$$$ times. In addition, each ball needs at least $$$O(n)$$$ moves to travel, so we get $$$O(nm + nk)$$$.
We can improve this further. You can speed up each drops by storing consecutive $$$2$$$-cell segments in the downwards direction for each column. Using a Disjoint-Set Union data structure, for each cell $$$a_{x,y} = 2$$$, join it with its bottom cell if $$$a_{x + 1, y} = 2$$$.
Time complexity: $$$O(k + rc\cdot\alpha(rc))$$$
1575K. Knitting Batik
Author: hocky
Developer: hocky
Editorialist: hocky
October the 2nd is the National Batik Day of Indonesia
Observe that only some several non-intersecting part of $$$nm - rc$$$ that is independent in the grid. Simple casework shows that the answer is $$$k^{nm}$$$ if $$$a = b$$$, and $$$k^{nm - rc}$$$ otherwise.
Time complexity: $$$O(\log nm)$$$
1575L. Longest Array Deconstruction
Author: yz_
Developer: steven.novaryo
Editorialist: steven.novaryo
Define $$$a'$$$ as the array we get after removing some elements in $$$a$$$ and valid element as $$$a'_i$$$ that satisfy $$$a'_i = i$$$.
We can try to find combination of indices $$${c_1, c_2, \dots c_m}$$$ such that $$$a_{c_i} = a'_{p_i} = p_i$$$ for a certain set $$${p_1, p_2, \dots p_m}$$$. In other words, we want to find all indices $$${c_1, c_2, \dots c_m}$$$ such that $$$a_{c_i}$$$ will be a valid element in the $$$a'$$$.
Observe that each element in $$$c$$$ and every pair $$$i$$$ and $$$j$$$ ($$$i < j$$$) must satisfy:
1. $$$c_i < c_j$$$
2. $$$a_{c_i} < a_{c_j}$$$
3. $$$c_i - a_{c_i} \leq c_j - a_{c_j}$$$, the element you need to remove to adjust $$$a_{c_i}$$$ to it's location is smaller than $$$a_{c_j}$$$.
Therefore, we can convert each index into $$$(c_i, a_{c_i}, c_i - a_{c_i})$$$ and find the longest sequence of those tuples that satisfy the conditions. This is sufficient with divide and conquer in $$$O(n\log n\log n)$$$.
But the solution can be improved further. Notice that if $$$(2) \land (3) \implies (1)$$$. Hence we can solve problem by finding the longest sequence of pairs ($$$a_{c_i}, c_i - a_{c_i}$$$) with any standard LIS algorithm.
Time complexity: $$$O(n\log n)$$$
1575M. Managing Telephone Poles
Author: yz_
Developer: steven.novaryo
Editorialist: steven.novaryo
Interestingly, if you generate the Voronoi Diagram and transcribe it to a grid, then the same connected area in the Voronoi Diagram is not necessarily in the same 8-connected component in the grid. This is why most Dijkstra solutions will get WA.
We can use convex hull trick to solve this problem.
Suppose that we only need to calculate $$$\sum_{x = 0}^{m} {S(x, y)}$$$ for a certain $$$y$$$. For a fixed $$$y$$$ axis and a pole located in point $$$(x_i, y_i)$$$, define $$$f(x) = (x - x_i)^2 + (y - y_i)^2 = - 2xx_i + x^2 - x_i^2 + (y - y_i)^2$$$, which is the euclidean distance of point $$$(x, y)$$$ and pole $$$(x_i, y_i)$$$.
Notice that, for a fixed pole $$$i$$$ and axis $$$y$$$, $$$f(x)$$$ is a line equation, thus we can maintain it with convex hull trick.
Additionally, for a certain $$$y$$$, there are only $$$m$$$ poles that we need to consider. More specifically, pole $$$(x_i, y_i)$$$ is called considerable if there is no other pole $$$(x_j, y_j)$$$ such that $$$x_i = x_j$$$ and $$$|y_i - y| < |y_j - y|$$$.
Hence we can find the $$$\sum_{x = 0}^{m} {S(x, y)}$$$ for a certain $$$y$$$ in $$$O(m)$$$ or $$$O(m \log m)$$$. Calculating $$$\sum_{x = 0}^{m} {S(x, y)}$$$ for all $$$y$$$ will result in $$$O(nm)$$$ or $$$O(nm \log m)$$$ time complexity.





