I wrote about the easy implementation of centroid decomposition on a tree.
Japanese here: http://www.learning-algorithms.com/entry/2018/01/20/031005
First of all, the implementation of centroid decomposition tends to be complicated, and you might have seen someone's code which has too many functions named 'dfs n' (n = 1, 2, 3, ...). I, for one, don't want to code something like that!
So, let me introduce my implementation of centroid decompositon. I hope you get something new from it.
Firstly, we need to know one of the centroids of the tree. Be careful not to forget that some vertices are going to die while repeating the decompositon.
The function which returns the centroid is easily implemented in the following way:
int OneCentroid(int root, const vector<vector<int>> &g, const vector<bool> &dead) {
static vector<int> sz(g.size());
function<void (int, int)> get_sz = [&](int u, int prev) {
sz[u] = 1;
for (auto v : g[u]) if (v != prev && !dead[v]) {
get_sz(v, u);
sz[u] += sz[v];
}
};
get_sz(root, -1);
int n = sz[root];
function<int (int, int)> dfs = [&](int u, int prev) {
for (auto v : g[u]) if (v != prev && !dead[v]) {
if (sz[v] > n / 2) {
return dfs(v, u);
}
}
return u;
};
return dfs(root, -1);
}
Then, using this centroid, you can implement centroid decomposition like this.
void CentroidDecomposition(const vector<vector<int>> &g) {
int n = (int) g.size();
vector<bool> dead(n, false);
function<void (int)> rec = [&](int start) {
int c = OneCentroid(start, g, dead); //2
dead[c] = true; //2
for (auto u : g[c]) if (!dead[u]) {
rec(u); //3
}
/*
compute something with the centroid //4
*/
dead[c] = false; //5
};
rec(0); //1
}
This works following way:
Calculate on the entire tree. All the vertices are alive now.
Find the centroid of the current tree, and make it die.
Calculate on the subtree which doesn't include the centroid. Go to 2 with this subtree.
Calculate something required which includes the centroid.
Make the centroid alive again, because this is DFS.
Simply enough, when you use this, you just need to change the part 4. All the other parts are the same, which means you can use it generally.
Let me show you an example.
https://beta.atcoder.jp/contests/yahoo-procon2018-final-open/tasks/yahoo_procon2018_final_c
(I guess this statement is available only in Japanese. Sorry for inconvenience!)
Summary: You are given a tree with N vertices. Answer the Q queries below.
Query v k : Find the number of the vertices, such that the distance from v is exactly k.
N, Q ≤ 105
The obvious solution to this problem is, for each query v, k, make v-rooted tree and count the number of the vertices whose depth is equal to k. This solution, however, requires time O(NQ).
When you want to count something on a tree, especially when it's related to a path, centroid decomposition is one of the good directions you are heading for.
First of all, let all the queries on the tree, and deal with them all at once. It's easy to see that these queries are actually asking the number of the paths whose length is k and the end point is v.
If you decompose the tree, as I mentioned above, you only need to count the paths which include the centroid.
More specifically, just calculate the the number of the distances from the centroid, and make the paths whose length is exacly k, and count them. Again, I didn't change almost anything but the part 4 of the implementation above.
#include <cstdio>
#include <vector>
#include <algorithm>
#include <functional>
#include <map>
#include <cassert>
#include <cmath>
using namespace std;
int OneCentroid(int root, const vector<vector<int>> &g, const vector<bool> &dead) {
static vector<int> sz(g.size());
function<void (int, int)> get_sz = [&](int u, int prev) {
sz[u] = 1;
for (auto v : g[u]) if (v != prev && !dead[v]) {
get_sz(v, u);
sz[u] += sz[v];
}
};
get_sz(root, -1);
int n = sz[root];
function<int (int, int)> dfs = [&](int u, int prev) {
for (auto v : g[u]) if (v != prev && !dead[v]) {
if (sz[v] > n / 2) {
return dfs(v, u);
}
}
return u;
};
return dfs(root, -1);
}
vector<int> CentroidDecomposition(const vector<vector<int>> &g, const vector<vector<pair<int, int>>> &l, int q) {
int n = (int) g.size();
vector<int> ans(q, 0);
vector<bool> dead(n, false);
function<void (int)> rec = [&](int start) {
int c = OneCentroid(start, g, dead);
dead[c] = true;
for (auto u : g[c]) if (!dead[u]) {
rec(u);
}
/*
changed from here
*/
map<int, int> cnt;
function<void (int, int, int, bool)> add_cnt = [&](int u, int prev, int d, bool add) {
cnt[d] += (add ? 1 : -1);
for (auto v : g[u]) if (v != prev && !dead[v]) {
add_cnt(v, u, d + 1, add);
}
};
function<void (int, int, int)> calc = [&](int u, int prev, int d) {
for (auto it : l[u]) {
int dd, idx;
tie(dd, idx) = it;
if (dd - d >= 0 && cnt.count(dd - d)) {
ans[idx] += cnt[dd - d];
}
}
for (auto v : g[u]) if (v != prev && !dead[v]) {
calc(v, u, d + 1);
}
};
add_cnt(c, -1, 0, true);
for (auto it : l[c]) {
int dd, idx;
tie(dd, idx) = it;
ans[idx] += cnt[dd];
}
for (auto u : g[c]) if (!dead[u]) {
add_cnt(u, c, 1, false);
calc(u, c, 1);
add_cnt(u, c, 1, true);
}
//
dead[c] = false;
};
rec(0);
return ans;
}
int main() {
int n, q;
scanf("%d %d", &n, &q);
vector<vector<int>> g(n);
for (int i = 0; i < n - 1; i ++) {
int a, b;
scanf("%d %d", &a, &b);
a --, b --;
g[a].push_back(b);
g[b].push_back(a);
}
vector<vector<pair<int, int>>> l(n); //dist, query idx
for (int i = 0; i < q; i ++) {
int v, k;
scanf("%d %d", &v, &k);
v --;
l[v].emplace_back(k, i);
}
auto ans = CentroidDecomposition(g, l, q);
for (int i = 0; i < q; i ++) {
printf("%d\n", ans[i]);
}
return 0;
}
You can practice centroid decomposition on these problems too! Try them if you would like!
http://codeforces.com/contest/914/problem/E
https://csacademy.com/contest/round-58/task/path-inversions
These problems ask you to count the number of the specific paths too.
Thank you for your reading!









 part of the entire grid.
part of the entire grid.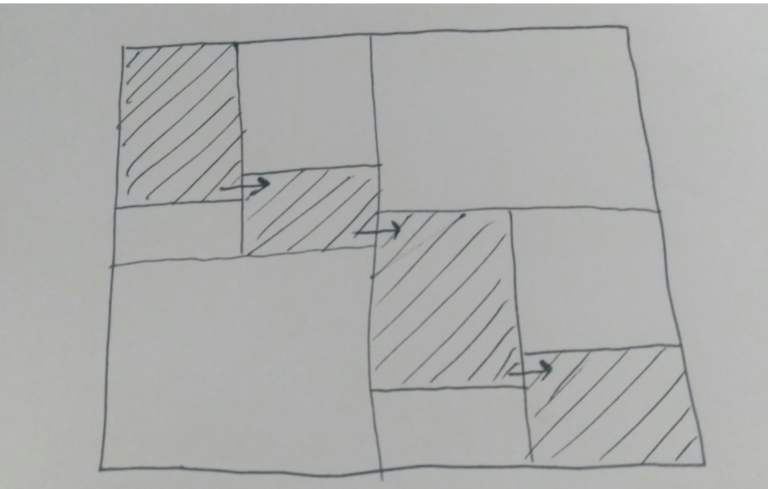
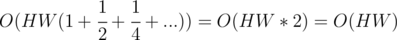
 , let me define
, let me define