UPD Editorial of problem E was added, I apologize for the delay. Hope you found it interesting.
A. Face Detection
Author: Monyura
One should iterate through each 2x2 square and check if it is possible to rearrange letters in such way they they form the word "face". It could be done i.e. by sorting all letters from the square in alphabetic order and comparing the result with the word "acef"(sorted letters of word "face").
B. Looksery Party
Author: Igor_Kudryashov
In any cases there is such set of people that if they come on party and send messages to their contacts then each employee receives the number of messages that is different from what Igor pointed. Let's show how to build such set. There are 2 cases.
There are no zeros among Igor's numbers. So if nobody comes on party then each employee receives 0 messages and, therefore, the desired set is empty.
There is at least one zero. Suppose Igor thinks that i-th employee will receive 0 messages. Then we should add i-th employee in the desired set. He will send messages to his contacts and will receive 1 message from himself. If we add other employees in the desired set then the number of messages that i-th employee will receive will not decrease so we can remove him from considering. Igor pointed some numbers for people from contact list of i-th employee and because they have already received one message we need to decrease these numbers by one. After that we can consider the same problem but with number of employees equals to n - 1. If the remaining number of employees is equal to 0 then the desired set is built.
C. The Game Of Parity
Author: olpetOdessaONU
If n = k no moves may be done. The winner is determined with starting parity of citizens' number. Otherwise let's see that the player making the last move may guarantee his victory, if there are both odd and even cities when he makes the move. He just selects the city of which parity he should burn to obtain required parity. So, his enemy's target is to destroy all the cities of some one type. Sometimes the type does matter, sometimes doesn't. It depends on the player's name and the parity of k. So the problem's solution consists in checking if "non-last" player's moves number (n - k) / 2 is enough to destroy all the odd or even cities. If Stannis makes the last move and k is even, Daenerys should burn all the odd or all the even cities. If k is odd, Daenerys should burn all the odd cities. If Daenerys makes the last move and k is even, Stannis has no chance to win. If k is odd, Stannis should burn all the even cities.
D. Haar Features
Author: Monyura
This problem had a complicated statement but it is very similar to the real description of the features. Assume that we have a solution. It means we have a sequence of prefix-rectangles and coefficients to multiply. We can sort that sequence by the bottom-right corner of the rectangle and feature's value wouldn't be changed. Now we could apply our operations from the last one to the first. To calculate the minimum number of operations we will iterate through each pixel starting from the bottom-right in any of the column-major or raw-major order. For each pixel we will maintain the coefficient with which it appears in the feature's value. Initially it is 0 for all. If the coefficient of the current cell is not equal to + 1 for W and - 1 for B we increment the required amount of operations. Now we should make coefficient to have a proper value. Assume that it has to be X( - 1 or + 1 depends on the color) but current coefficient of this pixel is C. Then we should anyway add this pixel's value to the feature's value with the coefficient X - C. But the only way to add this pixel's value now(after skipping all pixels that have not smaller index of both row and column) is to get sum on the prefix rectangle with the bottom-left corner in this pixel. Doing this addition we also add X - C to the coefficient of all pixels in prefix-rectangle. This solution could be implemented as I describe above in O(n2m2) or O(nm).
Also I want to notice that in real Haar-like features one applies them not to the whole image but to the part of the image. Anyway, the minimum amount of operations could be calculated in the same way.
E. Sasha Circle
Authors: Krasnokutskiy, 2222
Author's solution has complexity  , where C is a maximum absolute value of the coordinates of all given points.
, where C is a maximum absolute value of the coordinates of all given points.
Let’s call a set of points A and B separable if there’s a circle inside or on the boundary of which lie all the points of one set. When there’re no points neither inside nor on the boundary of the circle we call this circle separating. Let points of the set A lie inside or on the boundary of the circle and points of the set B lie outside the circle. Points from set A are allowed to be on the boundary of the separative circle as after increasing radius a little we’re getting set A strictly inside and set B strictly outside the circle.
Let A contain at least two points. Separating circle can be compressed in such a way that it’ll pass at least through two points of the set A. It’s possible to look over all the pairs of points  and try to pass each pair through the separating circle. The centre of the desired circle lies on the medial perpendicular of the segment pq. Let’s designate the points of the medial perpendicular as l(t) where
and try to pass each pair through the separating circle. The centre of the desired circle lies on the medial perpendicular of the segment pq. Let’s designate the points of the medial perpendicular as l(t) where 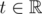 is a parameter. All the points that don’t lie on the straight line pq make parameter t bounded above or below. All the points that lie on the straight line pq have to lie outside the limits of the segment pq. E.g. a picture below displays a blue point which bounds the centre of separating circle from the left side and red points – from the right side. That’s why the centre has to lie inside a segment cd.
is a parameter. All the points that don’t lie on the straight line pq make parameter t bounded above or below. All the points that lie on the straight line pq have to lie outside the limits of the segment pq. E.g. a picture below displays a blue point which bounds the centre of separating circle from the left side and red points – from the right side. That’s why the centre has to lie inside a segment cd.
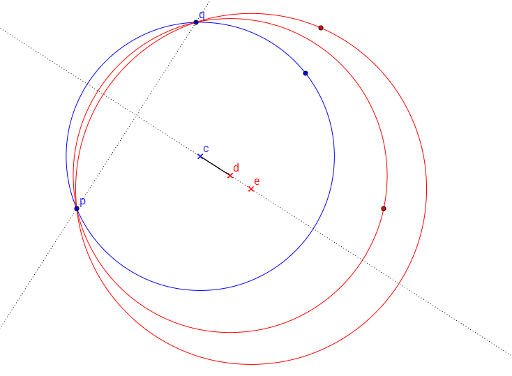
Let’s look over all the points to make sure that a value t which satisfies all the bounds exists. This provides us with the problem solving for O((|A|2 + |B|2)(|A| + |B|)).
Let’s examine paraboloid z = x2 + y2 and draw arbitrary non-vertical plane ax + by + z = c. The intersection of the paraboloid and the plane satysfies the equation ax + by + x2 + y2 = c, or 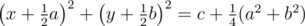 . If project points of the paraboloid (x, y, x2 + y2) onto the plane
. If project points of the paraboloid (x, y, x2 + y2) onto the plane 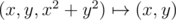 the cross-section of the paraboloid formed by the plane projects onto a circle, the paraboloid points below the plane projects onto internal points of the circle, those above the plane projects onto points outside the circle. As
the cross-section of the paraboloid formed by the plane projects onto a circle, the paraboloid points below the plane projects onto internal points of the circle, those above the plane projects onto points outside the circle. As  is one-to-one correspondence the opposite is also true: when points of the plane project onto the paraboloid
is one-to-one correspondence the opposite is also true: when points of the plane project onto the paraboloid 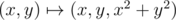 the plane projects onto the cross-section of the paraboloid formed by the plane, the internal points – onto the paraboloid below the cross-section and external points – above the cross-section.
the plane projects onto the cross-section of the paraboloid formed by the plane, the internal points – onto the paraboloid below the cross-section and external points – above the cross-section.
So, projection of points onto paraboloid assigns one-to-one correspondence between circles and planes (non-vertical). partitioning of sets of points A and B of plane by circle can be done by means of partitioning of their three-dimensional projections into paraboloid A′ and B′ by non-vertical plane. Let’s call such a plane separating (like separating circle, separating plane can include points from A′).
By analogy with separating, circle separating plane can be passed through two points of set A′. All the other points of A′ will lie below or on the plane. In other words separating plane will pass through the edge of the upper convex hull of the set A′. The projection of edges of the upper convex hull A′ onto the plane xOy will produce some sort of a set flat convex hull partitioning into A by non-intersecting edges. In this case separating plane corresponds separating circle passing through the edge partition. Let’s designate the convex hull A as coA. In case when none of 4 vertices coA lies within one circle all the edges of the upper convex hull are triangles and the derived partitioning is triangulation. Otherwise the derived partitioning should be completed to be triangulation.

To construct a separating circle look over triangulation edges and check the possibility of drawing a circle though an edge as it is described above.
The derived triangulation has the following feature: circle drawn around any triangle contains the whole polygon coA as the corresponding bound of three-dimensional convex hull is higher than all three-dimensional points A′. The described triangulation is “opposite” to the Delaunay triangulation according to which circle drawn around any triangle doesn’t contain any points of the original set. This triangulation is commonly known as the Anti-Delaunay triangulation.
Using the characterizing feature the Anti-Delaunay triangulation can be constructed by means of the method “divide and conquer” without transferring into three-dimensional space and working with points of plane and circles only. Let us triangulate polygon created by the vertices coA when moving counter-clock-wise from i to j. Let us find the third point of triangle, that will contain edge (i, j). I.e such point k, that circumscribed circle over triangle (i, j, k) contains the whole current polygon. For this purpose let’s iterate through all polygon’s vertices and select the one, that gives the extreme position of the center of the circumscribed circle lied on the mid-perpendicular of (i, j). The circle will contain the whole polygon coA as the edge (i, j) is included in the Anti-Delaunay triangulation. Recursively triangulate polygons with vertices from i to k and from k to j. The base of recursion is a segment, that shouldn't be triangulated.
To solve the original problem one should swap A and B and perform the above procedure once more. Complexity of the algorithm is O(|A|log|A| + |coA|(|coA| + |B|) + |B|log|B| + |coB|(|coB| + |A|)= , where C is a maximum absolute value of the coordinates of all given points. Actually, O(C3 / 2) is an estimation of the number of points at a convex hull with no three points in a line.
, where C is a maximum absolute value of the coordinates of all given points. Actually, O(C3 / 2) is an estimation of the number of points at a convex hull with no three points in a line.
F. Yura and Developers
Authors: Rubanenko
Let's consider following solution:
Let f(l, r) be the solution for [l, r] subarray. It's easy to see that f(1, n) is the answer for the given problem. How should one count f(l, r)? Let m be an index of the maximum value over subarray [l, r]. All the good segments can be divided into two non-intersecting sets: those that contain m and those that don't. To count the latter we can call f(l, m - 1) and f(m + 1, r). We are left with counting the number of subarrays that contain m, i.e. the number of pairs (i, j) such that l ≤ i < m < j ≤ r and g(i, m - 1) + g(m + 1, j)%k = 0 (g(s, t) defines as + as + 1 + ... + at). Let s be the sequence of partial sums of the given array, i.e. si = a1 + a2 + ... + ai. For every j we are interested in the number of such i that sj - si - am%k = 0, so if we iterate over every possible j, then we are interested in number of i that si = sj - am(modk) and l ≤ i < m. So we are left with simple query over the segment problem of form "how many numbers equal to x and belong to a given segment (l, r)". It can be done in O(q + k) time and memory, where q is the number of generated queries. Model solution processes all the queries in offline mode, using frequency array.
One can notice that in the worst case we can generate O(n2) queries which doesn't fit into TL or ML. However, we can choose which is faster: iterate over all possible j or i. In both cases we get an easy congruence which ends up as a query described above. If we iterate only over the smaller segment, every time we "look at" the element w it moves to a smaller segment which is at least two times smaller than the previous one. So, every element will end up in 1-element length segment where recursion will meet it's base in O(log(n)) "looking at" this element.
The overall complexity is O(n × log(n) + k).
G. Happy Line
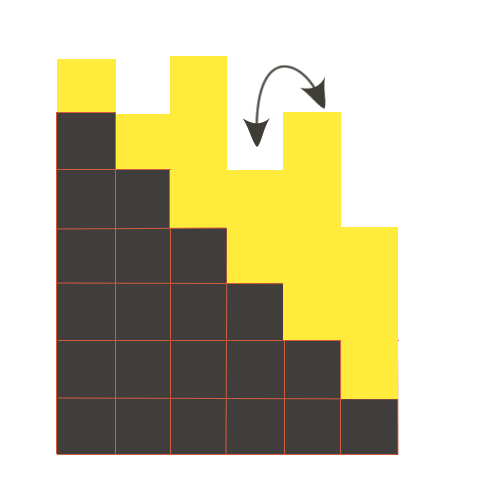
Let's reformulate the condition in terms of a certain height the towers, which will be on the stairs. Then an appropriate amount of money of a person in the queue is equal to the height of the tower with the height of the step at which the tower stands. And the process of moving in the queue will be equivalent to raising a tower on the top step, and the one in whose place it came up — down. As shown in the illustrations. Then, it becomes apparent that to make all of the tower on the steps to be sorted, it is enough to sort the tower without the height of step it stays. Total complexity of sorting is O(nlog(n)).

H. Degenerate Matrix
Author: Igor_Kudryashov
The rows of degenerate matrix are linear dependent so the matrix B can be written in the following way:
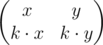
Suppose

Let's assume that elements of the first row of matrix A are coordinates of point a0 on two-dimensional plane and the elements of the second row are coordinates of point a1. Assume that the rows of matrix B are also coordinates of points b0 and b1. Let's note that in this case the line that is passing through points b0 and b1 is also passing through point (0, 0).
Let's find the answer — the number d — by using binary search. Suppose we are considering some number d0. We need to check if there is such matrix B that

In geometric interpretation it means that point b0 are inside the square which center is point a0 and length of side is 2·d0. In the same way the point b1 are inside the square which center is point a1 and length of side is 2·d0. So we need to check if there is a line that is passing through point (0, 0) and is crossing these squares. In order to do this we should consider every vertex of the first square, build the line that is passing through the chosen vertex and the center of coordinate plane and check if it cross any side of the other square. Afterwards we should swap the squares and check again. Finally if there is a desired line we need to reduce the search area and to expand otherwise.








 I am glad to announce Looksery Cup 2015, that is prepared by our developers, each one of them has made a great impact:
I am glad to announce Looksery Cup 2015, that is prepared by our developers, each one of them has made a great impact: 


