The Benelux Algorithm Programming Contest 2020 takes place December 12th. This is a subregional contest for teams from Belgium, the Netherlands and Luxembourg, which feeds into NWERC.
More info can be found here. There is an online mirror open to all here. The online mirror contest starts 12:30 CET. The whole contest is in English. Sorry for the short notice!









 time? (or optionally with some extra
time? (or optionally with some extra 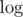 -factors) In particular,
-factors) In particular, 
