Hi!
For this problem for each light j you could just iterate over all pressed buttons and find the first button bi that bi < j. Then you could output bi and move to next light.
For this problem you can find the number of tokens you can save if you initally have k tokens in O(1). Then you can calculate the answer for all of numbers in O(n).
Suppose 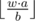 by p. then p * b ≤ w * a. then
by p. then p * b ≤ w * a. then 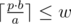 .
.
Suppose initially we have k tokens. Let  then we need to find such maximum k0 that
then we need to find such maximum k0 that 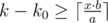 .
.
So k0 will be equal to 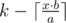 . so we can calculate k0 in O(1).
. so we can calculate k0 in O(1).
In each turn Bimokh will at least get one point so the result is at lease  . So if
. So if 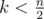 the answer is -1.
the answer is -1.
Let's denote 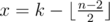 . Then you could output x and 2x as the first two integers in the sequence then output
. Then you could output x and 2x as the first two integers in the sequence then output 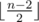 consecutive integers and also one random integer(distinct from the others) if n is odd. Based on the following fact, Bimokh's point will equal to
consecutive integers and also one random integer(distinct from the others) if n is odd. Based on the following fact, Bimokh's point will equal to 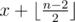 which is equal to k.
which is equal to k.
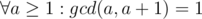 .
.
Also you must consider some corner cases such as when n = 1.
Lets define dp[i][j] as number of good sequences of length i that ends in j.
Let's denote divisors of j by x1, x2, ..., xl. Then 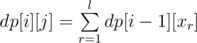
This yields O(nk sqrt(n)) solution which is not fast enough. But one could use the fact that the following loops run in O(n log(n)) in order to achieve O(nk log(n)) which is fast enough to pass the tests.
for (i = 1; i <= n; i++) //loop from 1 to n
for (int j = i; j <= n; j += i) //iterating through all multiples of i that are at most n
414C - Mashmokh and Reverse Operation
Build a complete binary tree with height n. So its i-th leaf corresponds to i-th element of the initial array. For each vertex v lets define its subarray as the subarray containing the elements that have a leaf corresponding to them in subtree rooted at v.
For each non-leaf vertex v, suppose its left child's subarray contains elements [a..b] of the array and its right child contains elements [b + 1..c] of the array. We'll calculate two numbers for this vertex. number of pairs (i, j)(a ≤ i ≤ b ≤ j ≤ c) that ai > bj and number of pairs (i, j)(a ≤ i ≤ b ≤ j ≤ c) that ai < bj. We'll call the first calculated number, normal number and the other one reverse number. Calculating these numbers can be done using merge-sort algorithm in O(n * 2n). We'll
Initially write normal number for each vertex on it. We'll define a vertex's type as type of the number that is written on them. Let's define height of a vertex v equal to its distnace to the nearest leaf. Also let's define switching a vertex as switching the number written on it with the other type number(if normal number is written on it change it to reverse number and vise-versa).
Initially sum of writed numbers is equal to number of inversions in the initial array. Now when query h is given, by switching all vertices with height at most h, the sum of writed numbers will become equal to the number of inversions in the new array. The only question is how to perform such query fast? One can notice that in a height h, always all of the vertices has the same type. So we can calculate two numbers for each height h. The sum of normal numbers of vertices with height h and the sum of their reverse numbers. Then instead of switching vertices in a height one by one each time, one can just switch the number for that height. The sum of numbers of heights after each query will be the answer for that query. since there are n height each query can be performed in O(n) so the total running time will be O(nq + n * 2n).
414D - Mashmokh and Water Tanks
Let's suppose instead of a tank there is a pile at each vertex and instead of water the game is played on tiles.
Let's denote distance of each vertex q from the root by depth(q). Also Let's label each tile with number of the vertex it was initially put on. Suppose initially there was a tile at each of vertices v and u and after some move tile u and v are in the same vertex's pile. Then one can prove that there were exactly |depth(v) - depth(u)| moves at which vertex containing the tile at vertex with less depth was closed and the vertex containing the other tile wasn't.
Suppose after i-th move, there was xi tiles inside the root's pile and xj is the maximum among these numbers. Suppose tiles a1, a2, ...axj were on the root after j-th move. Then the other tiles that we put inside the tree at the beginning have no effect in the final result. Then we can suppose that only these tiles were initially put on tree.
So we can assume that all tiles we place at the beginning will reach to the root together. Suppose hi of these tiles were put at a vertex with depth i and d1 is the maximum depth that there is at least a tile in that depth. So as to these tiles reach to the root together we must pay 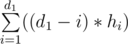 . Then we want to minimize the number of needed coins so at the beginning there must not be two consecutive depth i and i + 1 that i + 1 ≤ d and there is a tile at depth i and an empty vertex at depth i + 1. In other words if we denote the minimum depth that initially there is a tile inside it as d0 then there must be a tile at each vertex with depth more than d0 and less than or equal to d1.
. Then we want to minimize the number of needed coins so at the beginning there must not be two consecutive depth i and i + 1 that i + 1 ≤ d and there is a tile at depth i and an empty vertex at depth i + 1. In other words if we denote the minimum depth that initially there is a tile inside it as d0 then there must be a tile at each vertex with depth more than d0 and less than or equal to d1.
Let's iterate over d1. Then for each d1 we can calculate d2, the minimum depth that we can pay the needed price if we put a tile at each vertex with depth at least d2 and at most d1. Let's denote this needed price as p0. Then we can also put 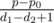 at depth d2 - 1. So we can calculate maximum number of tiles that we can put on the tree so that they all reach to root together for a fixed d1. So the maximum of these numbers for all possible d1 will be the answer.
at depth d2 - 1. So we can calculate maximum number of tiles that we can put on the tree so that they all reach to root together for a fixed d1. So the maximum of these numbers for all possible d1 will be the answer.
Since by increasing d1, d2 won't decrease one can use two-pointers to update d2 while iterating over d1. Let's denote number of the vertices with depth i as cnti. Then we can save and update the following values.
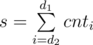

Then the needed price is equal to (d1 * s) - t. So as long as (d1 * s) - t > p we must increase d2. This yields an O(n) solution.
414E - Mashmokh's Designed Problem
Let's define the dfs-order of a tree as the sequence created by calling function dfs(root). We'll build another sequence from a dfs-order by replacing each vertex in dfs-order by '+1' and inserting a '-1' after the last vertex of its subtree. Note that all vertices of a particular subtree are a continuous part of dfs-order of that tree. Also note that for each vertex v if the +1 corresponding to it is the i-th element of sequence, then v's distance from root(which we'll denote by height of v) is equal to sum of elements 1..i.
Suppose we can perform the following operations on such sequence:
For each i, find sum of the elements 1..i.
For each i find the biggest j(j < i) so that sum of elements 1..j of the sequence equals p.
Using these two operations we can find LCA of two vertices v and u, so since distance of u and v equals to height(u) + height(v) - 2 * height(LCA(u, v)) we can answer the second query. Also the third query can be answered using the second operation described above.
As for the first query it cuts a continuous part of sequence and insert it in another place. This operation can be done using implicit treap. Also we can use the treap as a segment tree to store the following values for each vertex v. Then using these values the operations described above can be done. All of these operation can be done in O(logn).
Sum of the elements in its subtree(each vertex in the treap has a value equal to +1 or -1 since it corresponds to an element of the sequence.)
Let's write the values of each vertex in the subtree of v in the order they appear in the sequence. Then lets denote sum of the first i numbers we wrote as ps[i] and call elements of ps, prefix sums of the subtree of v. Then we store the maximum number amongst the prefix sums.
Also we'll store the minimum number amongst prefix sums.










I can't wait this editorial more~ great pleased for its coming... And thanks for such nice contest. Waiting for div1C and E~
for problem C: consider the segment tree(the tree itself) of the array.let I be the interval of this node Ir the interval of it's right child and Il the interval of it's left child.let d be the number of inversions such that first element belongs to Il and the other belongs to Ir(d = |{(x,y):x < y,x E Il, y E Ir}| ), and let p = |{(x,y):x < y,x E Ir,y E Il}| (E stands for belonging). let D[i] = sum of nodes from the ith level's d and P[i] = sum of nodes from the ith level's p(root is in the first level). obviously when we do the operations if we update the D[i]s then we can print the sum of them as the answer.when an operation happens whit input q the D[1] -> D[n — q] remain the same while you can understand D[n — q + 1] -> D[n + 1] are swapped with P[n — q + 1] -> P[n + 1] (swap(D[n — q + 1], P[n — q + 1]),... , swap(D[n + 1],P[n + 1])). because the number of D[i]s is at most 20 so each step can be done with 40(at most) operations. you can use merge sort algorithm to find d, p.
you can find an implementation of this here.
great explanation, thanks.
nice algorithm! thx~
414B i use prime factorization and combinatorics, it works quite good :)
That is a lot of code. DP is shorter. 6279086
What are you doing with the mods here?
It just takes mod
MOD. I was trying to make it faster I guess. I'm not even sure if integer-dividing then multipling is faster than just taking mod using%.Does anyone know?
please tell me know if you know that now.
Here's my DP solution. It takes O(n*k). 6294472
That's O(n*k*ln n)
Sieve of Eratosthenes is not needed in div. 1 B after all. Precalc of divisors of each number from range [1..2001] could be done simply in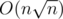 or in
or in 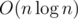 . But also there is a following fact:
. But also there is a following fact:
This loop will work for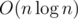 , because it is the sum of the harmonic series. So we could simply solve this problem even without precalc of divisors in
, because it is the sum of the harmonic series. So we could simply solve this problem even without precalc of divisors in 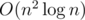 . Like in this submission: 6274315
. Like in this submission: 6274315
This is what I meant actually.
I updated the post. Sorry for the misunderstanding caused.
I cannot understand how did you find factors of i in logn . I am a beginner , can you explain this more clearly?
B can be easily solved in O(n log^2(n)) if we notice that the sequence can't have more than O(log n) distinct elements, do a DP for strictly increasing sequences and then use simple combinatorics to get the answer.
The constraints are a little weird: I wasn't sure if an O(n^2 log n) solution was supposed to fit or if O(n log^2 n) solution was intended. I don't like this kind of constraints that make the contestant decide between taking risk implementing the simple solution or wasting time implementing the fast one. Well, in this case the fast solution was almost no harder than the simple one, so I have nothing to complain about :)
А почему различных элементов в последовательности не может быть более logN ?
because i-th number in "good" sequence is at least (i-1)-th number * 2.So sequence can't have more than O(log n) distinct elements.
thanks.
Is combinatorics necessary for solving this problem ? I'm a beginner in DP so I just wanted to know whether I should learn combinatorics and come back to solve this problem or it can be solved without combinatorics .
i am the god of combinatorics
if u want to learn come to me
Sorry for necroposting. Can you please explain your O(n*log^2(n)) dp approach? I could understand the intended solution and am curious to know the faster approach as well.
Let's call a sequence excellent if it's both good and strictly increasing. Each good sequence can be seen as an excellent sequence with some duplicates added, e.g. [1, 3, 6, 12] -> [1, 1, 3, 6, 6, 6, 12, 12]. We can count excellent sequences of each length i <= k, then multiply it by the number of ways to add duplicates to reach length k.
How many ways are there to extend an excellent sequence of length i to a good sequence of length k? Consider the positions of first occurrence of each unique number in the new sequence. The first number is always at the first position. The others can be in any i-1 out of k-1 positions. These positions uniquely determine the good sequence. E.g. ([1, 3, 6, 12], [*, -, *, *, -, -, *, -]) <-> [1, 1, 3, 6, 6, 6, 12, 12]. So the answer is the binomial coefficient $$${k-1}\choose{i-1}$$$.
Number of excellent sequences of each length can be calculated using the same dp as in the OP, but "int j = i" is replaced with "int j = i*2", and i only goes up to log_2(n)+1 because there are no excellent sequences longer than that (because each element is at least 2x the previous one).
Thanks a lot. Got the idea, implemented it and ACed as well.
please could you write the solution of last three problems quickly as possible ?
For Div 2 B I used
((a*x) % b) / a. Can someone tell why this is wrong?because you used
intfor your variables. Change them tolong longand you'll get accepted.God dammit :( :(
Superty, rather than ask to forum you can see at your submission history.
it's very clearly on the test 4 that you're answer is negative, it's indicating that int can take it up.
:D
BTW, i don't understand why the formula is (((x * A) % B) / A ) in my opinion it should be ((x * A) % B). could you tell me about that. :D
(x*a)%bgives the maximum amount by which x*a can be reduced. So the maximum amount by which we can reduce x is given by((x*a)%b)/a(x*a)%bgives the maximum amount by which x*a can be reduced. If we reduce by more than that then we won't get maximum value of money. So the maximum amount by which we can reduce x is given by((x*a)%b)/aI still confuse.`
Can you give TC that will show the fact up?
:D
Try
1 2 9 5
the answer should be 0. But your formula
((x * A) % B)return 11 2 9 5?
what is the A and B?
1 2 9
5
with N=1, A=2, B=9, and x1=5
see (2*5)%9 = 1
For Ediv2 / Cdiv1 i come up with the fact that
number of inversion after reverse = N(N-1)/2 - number of inversion before reverse - number of pair of same elementBut still dunno how to make efficient solution with this. Can someone help me?
Actually this fact won't help you in this concrete problem. Because it wasn't mention in problem's statment about equal numbers in input. So for array [1, 1, 1, 1] you can't use it.
My accepted solution has the same idea. See code here.
About problem B (div 1), I had a different approach. Unfortunately, I missed the easier solution which costed me more time to implement.
The idea is the following DP: If N is the largest number in the sequence of length n and N = p1^a1 * p2^a2 * ... *pk^ak is it's prime factorization, then the answer depends on just a1, a2, ..., ak, n. So let's have a dynamic programming state (a1, a2, ..., ak, n). As n<=2000, n will have at most 4 prime divisors and it's easy to note that the total number of states is too small.
Finally, we have this formula: dp(a1, a2, a3, a4, n) = SUM_ALL( dp(b1, b2, b3, b4, n-1) : b1<=a1, b2<=a2, b3<=a3, b4<=a4).
The rest is too simple. This approach would work for even bigger constraints, for 20,000 and probably even more.
just remind that with n=2,000 you use more than 50% of the memory limit
Let me clarify: If we consider a1,a2,a3,a4 in decreasing order, then for n=2,000 we have a1<=10, a2<=5, a3<=3, a4<=1. So the memory will be the size of the array [11][6][4][2][2000]. I don't think that it's more than 50% of a memory limit.
Actually A(a1, a2, a3, ..., a_k) = A(a1) * A(a2) * ... * A(a_k).
6306167 Could someone point the bug in my code. I used binary search (from 1 to w) finding the smallest number which maximises money and saves tokens. I seem to be getting WA on 4th case. Can someone help me out here. Thanks.
You can try comparing with 6273974.
The condition for ansr[i] = 0 is ((num[i]*a)%b) < a. This gets you till test case 24, but your binary search is still wrong somewhere
Actually ansr[i] = ((num[i]*a)%b)/a is a valid solution.
i have a solution for B that is O(n*log n* log n* log(10^9+7)). the time of this algorithm is independent of l and my solution solves problem for n=10^4 and l=10^18 in less than a second : 6306952
i fix ln in O(n) then calculate answer in O(log n* log (n)* log(10^9+7)): if (ln = p1^a1 * p2^a2 p3^a3 .... pk^ak) the answer is c(a1+l-1,a1)...*c(ak+l-1,ak). k is in O(log n) and the amount of each ai is from range [1 to log n]. we can calculate c(a,b) modulo x in O(b)*log(x) and i do it in my functions. this algorithm is in O( n long n log n *log (10^9+7)) but it is optimized and works less than a sec for n=10^4 and k=10^18.
waiting for the E...
Can someone explain please, why is the "tokens" problem (problem B, division 2) supposed to be resolved using binary search (its even tagged with "binary search", also some high standing people submitted solutions based on binary search).
I understand the solution based on formula: ((x*a)%b)/a works too, if proper attention is applied to data types to avoid overflow.
I guess its too late reply to your post, but yes the problem can be solved using binary search. Suppose available tokens = x Now we know maximum money,we can make is v = floor((x*a)/b). Now we can do a binary search with low =0 and high =x such that lowest token value,say 'y' which can give value of 'v'. Hence remaining tokens = x-y
Hope it makes sense. My solution
So I guess we'll never get the tutorial for E?
Sorry for the delay. I added some hints about the solution.
I don't understand the problem statement for Div2 B. The formula is floor((w-a)/b). For the first test case, you have 12 tokens on the 1st day and you have a=1 and b=4. The answer for 1st day should be 0, but if you don't save any tokens you get floor((12-1)/4) = 2 which is the same of floor((9-1)/4), so, as far as I could understand, you could actually save 3 tokens on the 1st day.
I know this is probably a silly interpretation mistake. But could anyone please clarify the statement for me? (for example: how is 1st day on 1st test case supposed to be 0?)
Thanks in advance!
I think you have the same initial issue as I did, and I guess its a font issue. The formula is to multiply by 'a', not to subtract it.
That's it, thanks.
Problem B DIV.2 could any one explain why this works: ((x * a) % b) / a and this don't!: (x * a) % b
Let's take the first sample test case to understand this in a better way:
On the second day, worker has only 6 tokens and can get maximum (6*1)/4 = 1 dollar for that day and thus he can save 2 tokens. (since he initially had 6 of them and he saves 2 by the end of the day, the formula (x*a)%b is valid in this case). Similarly on the other days, the number of tokens he save is always less than or equal to those he had.
Let's take another tricky case:
Now the worker has got just 1 token at the start of the day, and he can at max earn 2 dollar (since (x*a)/b = (1*8)/3)) and he can save 2 tokens((x*a)%b = (1*8)%3) also at the end of the day which contradicts the fact that he actually had just 1 token at the start of the day.
So if we divide ((x*a)%b) by a, we actually reduce the number of tokens by a factor of a which we have earlier multiplied and thus giving the correct answer which is ((1*8)%3)/8 = 0 tokens left at the end of the day.
Hope that helps :)
Is there any proof for " But one could use the fact that the following loops run in O(n log(n)) "
Take a look at the pattern, were going to count the iterations of each inner loop and then sum them all
First inner iteration => n iterations
Second inner iteration (i = 2) => n / 2 iterations because we are taking 'steps' of size 2
...
nth iterations (i = n) => 1 iteration
That gives
n + n/2 + n/3 + ... + 1
Then we can use integral calculus to show that this sum is never greater than n*log(n)
Hi guys, my code here work locally on my codeblock with gnu g++11 complier, but when i try to submit my code to CodeForces, it show run time error on test 1. This is link to my submission http://codeforces.com/contest/414/submission/23796769. Can you help me ? Thanks a lot !
that what i could find
for (int i=1; i<=2000; ++i)
vector size is 2000
so there is no index of 2000 it's just from 0 to 1999
How to solve 414B using factorization in O(nklong(n))?