miaowtin's blog

Stirling Transformations
By miaowtin, history, 10 months ago, In English

Hello, Codeforces!

1. Recently, adamant published an excellent blog Stirling numbers with fixed n and k. There he described an approach to them via generating functions.

In this (messy) blog, I want to share one useful technique on the example of Stirling numbers of the first kind.

2. We start with the definition of the Stirling transformation of a sequence $$$(x_n)$$$ is the following mapping

$$$\displaystyle \{x_n\} \xrightarrow{\quad Stirling\quad} \left\{ \sum_{k=0}^{n} s(n,k) x_k \right\}, $$$

where $$$s(n,k)$$$ is a first-kind Stirling number. Here we have a place of flexibility for our technique: we can choose any other function $$$f(n,k)$$$ instead of Stirling numbers, though it only sometimes turns out to be useful.

3. The essence of this method is to find the transition formulae between Stirling transformations of a sequence $$$(x_n)$$$ and the sequence of its finite differences (one can think of it as a discrete analogue of derivative) $$$(y_n)$$$ defined by

$$$\displaystyle \{x_n\} \xrightarrow{\quad \Delta\quad} \{x_{n+1}-x_n\}. $$$

The acquaintance with finite differences is highly recommended for the readers of this blog.

Theorem 1 (Transition formulae). In fact, the following transition formulae hold:

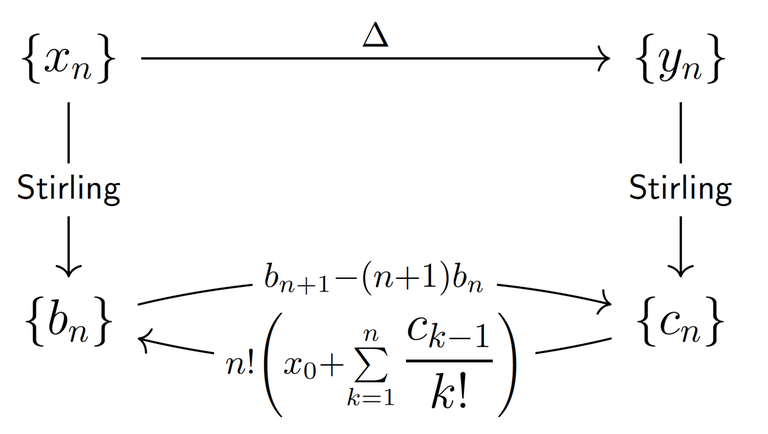
drawing

Step 1. How to work with finite differences?

Theorem 2 (solving first-order linear difference equation). Let $$$(y_k)$$$ be a recurrence relation that satisfies

$$$\displaystyle y_{k+1} = p_k y_{k} + q_k, $$$

where $$$(p_k), (q_k)$$$ are given sequences and there is no $$$i$$$ such that $$$p_i=0$$$, then the solution to this equation is given by

$$$\displaystyle y_k = \prod_{j=0}^{k-1} p_j \left( \sum_{j=0}^{k-1} \frac{q_j}{\prod_{\ell=0}^{j} p_\ell } + C\right) $$$
Proof

Step 2. Proof of the Theorem 1.

Proof

4. Using these transition formulae we can derive countless identities with Stirling numbers of the first kind (as well as identities involving binomial coefficients and other interesting combinatorial functions, as pointed out in 2). For example, taking $$$x_n = 1$$$, we obtain the following nice identity

$$$\displaystyle \sum_{k=0}^{n} s(n,k) = n! $$$

visualised by the diagram

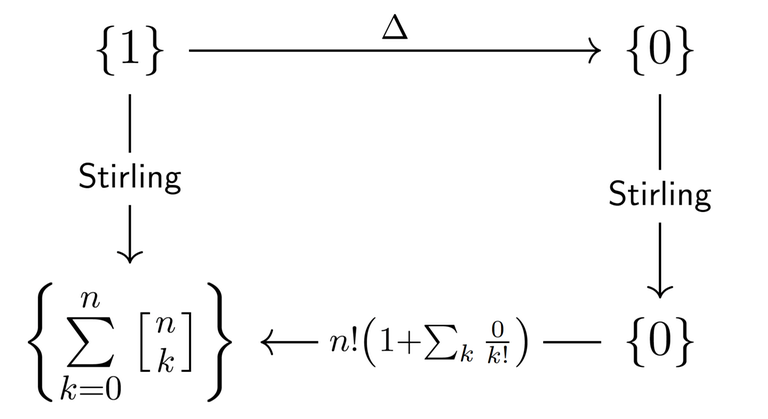
drawing

5. A nontrivial and interesting example. We exploit the combinatorial nature of $$$s(n,k)$$$ to write down the average number of cycles in a random permutation.

$$$\displaystyle \mathbf{E}[cycles] = \sum_{k=0}^{n} k \frac{s(n,k)}{n!} = \frac{\sum\limits_{k=0}^{n} k s(n,k)}{n!}. $$$

We can easily find the sum in the numerator by applying theorem 1 to the sequence $$$x_n = n$$$.

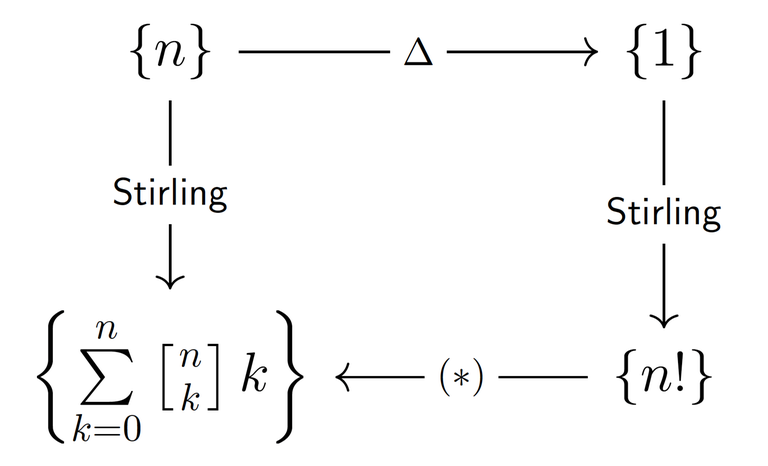
drawing
where the ($$$\ast$$$) is given by the following formula
$$$\displaystyle \sum\limits_{k=0}^{n} k s(n,k) = n!\sum_{k=1}^{n} \frac{(k-1)!}{k!} = n!H_n, $$$

where $$$H_n = 1 + 1/2 + \dots + 1/n$$$ is $$$n$$$-th Harmonic number. Hence $$$\mathbf{E}[cycles]=H_n=O(\log n)$$$, a very nice result!

Exercise

6. We generalise 5 and 6 by consider the sequence $$$x_n = n^k$$$ for a fixed $$$k$$$. From adamant's blog (highly connected with this section), we know that first-kind Stirling numbers behave much better with falling factorials. So, in order to find a good formula for the Stirling transformation of $$$n^k$$$, we first find it for $$$(n)_k$$$ and then apply

$$$\displaystyle n^k = \sum_{j=0}^{k} S(n,j) (n)_j. $$$

and derive the desired formula.

The details are left for the reader, here is the outline.

Step 1. Prove the identity $$$\sum_{j=0}^{N} s(j,k)/j! = 1/N! s(N+1,k+1)$$$ by double induction and Pascal-like identity (lemma 1).

Step 2. Apply Theorem 1 to $$$x_n=(n)_k$$$ (fix $$$k$$$) and using 1 prove that

$$$\displaystyle \sum_{n=0}^{N} s(N,n) (n)_k = k! s(N+1, k+1). $$$

Step 3. Finally, prove that

$$$\displaystyle \sum_{j=0}^{N} s(N,n) n^k = \sum_{j=1}^{k} S(k,j) s(N+1, j+1) j!. $$$

The last formula is obviously practical.

7 (Bonus).

Theorem 3 (transition between two kinds of Stirling numbers). Let $$$(a_n)$$$ be a sequence and

$$$\displaystyle b_n = \sum_{k=1}^{n} S(n,k) a_k $$$

be is second-kind Stirling transform. Then

$$$\displaystyle a_n = \sum_{k=1}^{n} (-1)^{n-k} s(n,k) b_k. $$$
Proof

8 (Remark). I mentioned twice that this method can be generalised. For example, for the binomial transformation

$$$\displaystyle \{x_n\} \xrightarrow{\quad Binom\quad} \left\{ \sum_{k=0}^{n} \binom{n}{k} x_k \right\}, $$$

the main theorem will be the following

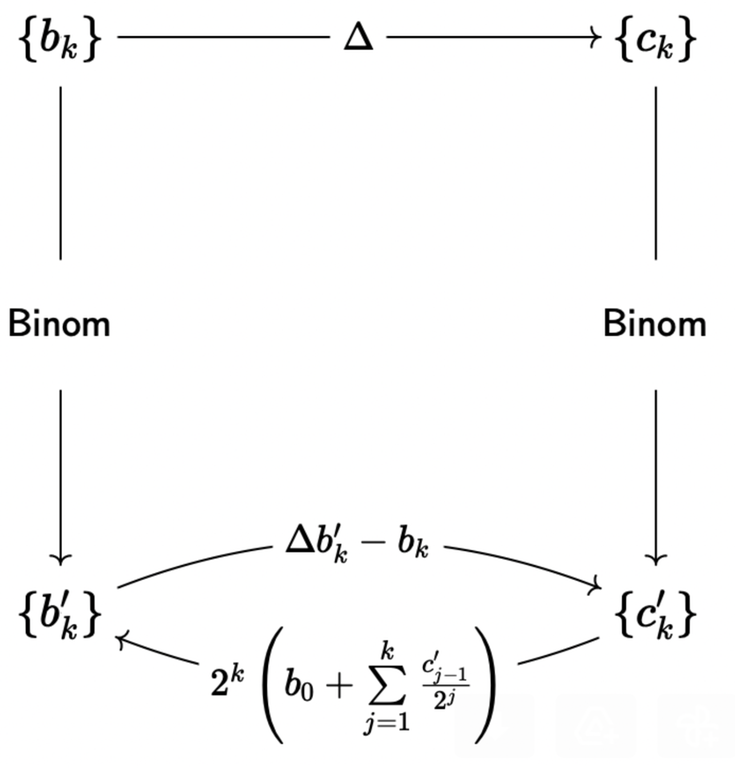
drawing

Using a similar strategy as in 6, we can prove that

$$$\displaystyle \sum_{n=0}^{N} \binom{N}{n} n^k = \sum_{j=0}^{k} S(k,j) \binom{n}{j} j! 2^{N-j}. $$$
  • Vote: I like it
  • +85
  • Vote: I do not like it

»
10 months ago, # |
  Vote: I like it +3 Vote: I do not like it

Is this based on this article? Quite nice presentation! Yet, I generally don't like direct work with coefficients, so I tried to understand e.g. what formulas for binomial transformation and finite differences mean in terms of EGF.

So, the binomial transformation is equivalent to multiplying EGF $$$A(x)$$$ with $$$e^x$$$:

$$$ A \mapsto e^x A. $$$

And finite differences, defined as $$$a_n \mapsto a_{n+1} - a_n$$$, correspond to the transform on EGF:

$$$ A \mapsto A' - A. $$$

So, the binomial transform of finite differences is $$$e^x( A' - A)$$$, while the binomial transform of the initial sequence is $$$e^x A$$$.

To express the binomial transform of finite differences through the binomial transform of original sequence, we notice

$$$ e^x(A' - A) = ((e^x A)' - e^x A) - e^x A, $$$

Meaning that the transform from $$$b_k'$$$ to $$$c_k'$$$ should, indeed, be $$$\Delta b_k' - b_k'$$$ (I assume, $$$\Delta b_k' - b_k$$$ is a typo).

Unfortunately, I don't have any clear ideas right now on how to do something similar with Stirling numbers, or even how to derive the inverse formulas or interpret them in terms of genfuncs...

→ Reply
  • »
    »
    10 months ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    Ok, I see why the inverse transform is messy. So, we know that

    $$$ F(x) = G'(x) - 2G(x). $$$

    How to get $$$G(x)$$$ from known $$$F(x)$$$? Well, it's just a linear diffeq, so there is a formula:

    $$$ G(x) = e^{2x} \int\limits e^{-2t} F(t) dt, $$$

    It probably yields the same result, but an easier way to solve it is, let $$$A(x)$$$ and $$$B(x)$$$ be the ordinary genfuncs of sequences, for which $$$F(x)$$$ and $$$G(x)$$$ are exponential genfuncs. Differentiation in EGFs translates to OGFs as

    $$$ G'(x) \mapsto \frac{B(x) - B(0)}{x}, $$$

    so we have

    $$$ B(x) = \frac{xA(x) + B(0)}{1-2x}, $$$

    which gives the same conversion formula between $$$b'_k$$$ and $$$c'_k$$$.

    → Reply
  • »
    »
    10 months ago, # ^ |
    ← Rev. 5   Vote: I like it +3 Vote: I do not like it

    Now, for Stirling transform, Wikipedia suggests that a proper representation, in terms of EGFs is

    $$$ A(x) \mapsto A(\log(1+x)). $$$

    I guess, it makes sense, as

    $$$ \sum\limits_{k=0}^\infty a_k \frac{x^k}{k!} \mapsto \sum\limits_{k=0}^\infty a_k \frac{\log(1+x)^k}{k!} = \sum\limits_{k=0}^\infty a_k \sum\limits_{n=k}^\infty s(n, k) \frac{x^n}{n!}, $$$

    given that $$$\frac{\log(1+x)^k}{k!}$$$ is the EGF for $$$s(n, k)$$$ with fixed $$$k$$$. So, the Stirling transform of finite differences is

    $$$ A'(\log(1+x)) - A(\log(1+x)). $$$

    Using $$$[A(\log(1+x))]' = \frac{A'(\log(1+x))}{1+x}$$$, we can re-express it as a function of $$$A(\log(1+x))$$$ as

    $$$ (1+x)[A(\log(1+x))]' - A(\log(1+x)) $$$

    Note that it corresponds to transition formula $$$c_n = b_{n+1} + (n-1) b_n$$$ instead of $$$c_n = b_{n+1} - (n+1) b_n$$$.

    This is because for signed Stirling numbers $$$s(n, k)$$$ the transition formula is

    $$$ s(n+1, k) = s(n, k-1) - n s(n, k) $$$

    instead of

    $$$ s(n+1, k) = s(n, k-1) + n s(n, k) $$$

    which was used in the blog.

    → Reply