The problem is to find the number of standing hamsters. If it is less than half, we should make the required number of hamsters standing. Otherwise we should make some hamsters sitting.
We can sort all the cities by their distance to the Tomsk city di. After that we are to find the smallest index t for which the total population p0 + p1 + ... + pt > = 106. In such case the answer is dt. We can sort all cities in O(NlogN) and find the value of t in O(N). Limits for N allow O(N2) sorting or any other O(N2) solution.
Consider the following formulas:
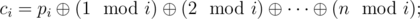
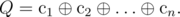
Let 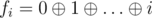 . Lets compute the following function for each i (0 ≤ i ≤ n). One can do it in O(n) using
. Lets compute the following function for each i (0 ≤ i ≤ n). One can do it in O(n) using 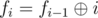 .
.
Lets transform ci:
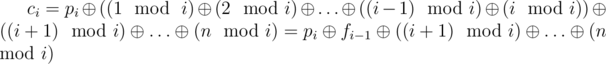
Also:
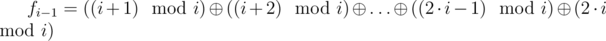
Thus:

That means, if n / i is odd, 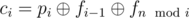 , otherwise —
, otherwise —  . ci can be computed in O(1), that's why the complexity of the whole solution — O(n).
. ci can be computed in O(1), that's why the complexity of the whole solution — O(n).
Due to the time limit for Java some of O(N4) solution got Accepted. The authors solution has complexity O(N3·logN). The main idea is to fix the top-border and bottom-border. Then, using some abstract data type, for each right-border we can find the most suitable left-border in O(logN) time. For example we can use set in C++ and its method lower_bound. For better understanding lets have a look at the following figure:
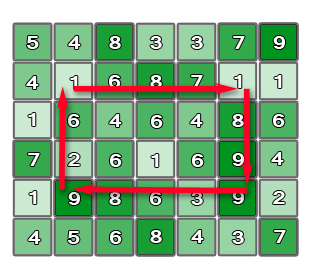
For such rectangle we fix the upper-border as row number 2 and bottom-border as row number 5. Also, we fix right-border as column number 6, and now we are to find some left-border. Now we can split the time value for any rectangle for two summands. One of them depends only on left-border and another one — on the right-border.

With the blue color the summand that depends only on the right-border is highlighted. With the red and yellow color — the other summand is highlighted. The red-colored value should be subtracted and the yellow-colored should be added. For any blue right-border's value we are to find the closest red-yellow left-border. That is the problem to be solved with the help of STL Set or any other similar abstract data type.
A classical DP-problem on finding expected number.
Lets define some function F(S) for some state — the expected number of minutes to finish the game from this state. For each color we can compute the probability of showing this color by the simple formula  , where c — the number of dice's faces of this color. Now we are to find the probability PL to stay in this state for the next minutes. That is the probabilty of showing black color plus the probabilities of showing colors with no blocks of that color to be removed from the tower. Now we can find the value via the following formula:
, where c — the number of dice's faces of this color. Now we are to find the probability PL to stay in this state for the next minutes. That is the probabilty of showing black color plus the probabilities of showing colors with no blocks of that color to be removed from the tower. Now we can find the value via the following formula:

The only problem is to find how to encode the state. To reduce the number of states we can assume that there is only 18 different type of levels, but not 27. For better time-performance it is better to use hashing. The solution for this problem requires good understanding of DP and quite good implementing skills.











i have a different approach for problem B.
binary search on (square of) the radius. and for a given radius, check if sum of all "neighbours" the circle encloses satisfies sum + s ≥ 106 or not.
my AC solution: 6470353
EDIT: my solution is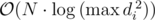 , slightly more complex than author's
, slightly more complex than author's  . ;)
. ;)
duplicate post
Nice approach
Problem A: "In one minute, Pasha can make some hamster ether sit down or stand up." I think in place of some you should use one. It cost me wrong answer during contest. Please look into the language ambiguities.
Thanks!
Sometimes it's better to look at samples first, especially for A div2. As I see, you was debugging it for ~30 minutes — don't do it with A div2) Start reading B after first two failed attempts. I did the same today, just because of stupid mistakes. After 20-minutes delay you will defenetly get accepted, even if statement will be written on esperanto.
Can someone explain the logic behind 424C — Magic formulas?
In my method, you can think about the associative property of xor and the cycle of modulo by some number~ ;)
In my solution, I first xor all pi as P = p1^...^pn, and precompute a xor array X[1...n], where X[i] = 1^...^i. Next, for each k=1,...,n, compute Tk = (1%k)^...^(n%k). Note that if n = k*t + r, where 0 ≤ r ≤ k - 1, then in Tk, each value in {1,..,r} appears t+1 times, and each value in {r+1,...k-1} appears t times. That means we can compute Tk in O(1) time given precomputed Xs above. For odd t, Tk = (r + 1)^...^(k - 1) = X[r]^X[k - 1], and for even t, Tk = X[r]. And finally we can compute the ans in O(n) time. You can see my solution for details: http://codeforces.com/contest/424/submission/6466539
Thanks a lot :D BTW you made a typo there X[r]^X[n] should be X[r]^X[k-1]. Really awesome explanation thanks!! :D
Thank for pointing out the typo. Fixed!
6476840
424D — Biathlon Track Do you mean you can do binary search to find the most suitable left border? Do you assume the perimeter will monotonically grow as you increase any given side?
He means you can use some data structure (e.g. set in C++) to find left border, which gives closest to given perimeter.
...
Never mind, I got it. Thanks.
can you tell me what you know ? i have the same problem. :)
Can you speak Russian?
I can, but I don't have Russian keyboard
I have the same problem, please help me out. Or give me a link of a proper soln which uses set for finding the closest left-border.
Your data in 424D is not strong enough. There is some Wrong Code also get an Accept, such as 6472530. There are 2 data I highly recommend to add. 6 3 0 0 10 10 1 1 1 1 1 1 1 3 1 1 3 1 1 3 1 1 1 1 should output:1 1 6 3. 3 6 0 0 10 10 1 1 1 1 1 1 1 1 3 3 3 1 1 1 1 1 1 1 should output:1 1 3 6.
can not agree more! the algorithm of binary search for this problem is wrong, but it can still get an accept.
Can someone please help me with Div2 Problem B.
The judge shows WA for the sample test case while it runs fine on my computer.
NOTE:
Why is this so? Here are my 2 submissions 9374428 and 9374522 Also it shows WA for my implementation using setprecision also.
Shouldn't the time complexity be mentioned in the Editorial? -_- i found the same solution for E but i couldn't calculate the complexity + i couldn't write a hash function for the grid which is TOTALLY missed in the editorial....... you didn't even explain the optimum way of playing which i assumed right without proof and came here looking for answers, some of these editorials need to be re-written by top competitors .....