sping128's blog

Looping through all subsets of a set of N elements
By sping128, 10 years ago, In English

This can be easily done by:

for (i = 0; i < 1<<N; i++) {
   ...
}

It will give us: 000, 001, 010, 011, 100, 101, 110, 111 in binary if N = 3

What if I want to loop in ascending order of the number of each subset's elements? For example, when N = 3, the order can be 000, 001, 010, 100, 011, 101, 110, 111 or 000, 001, 010, 100, 011, 110, 101, 111. Anyone knows the best way to do this?

  • Vote: I like it
  • +13
  • Vote: I do not like it

»
10 years ago, # |
← Rev. 2   Vote: I like it +19 Vote: I do not like it

Nice trick: it's likely that inside your loop you will do something with bits of the number in O(n) time. If so, you do not need to create bits-ascending order of the masks. You can just use following code with the same asymptotic:


for (int k = 0; k <= n; k++)
{
    for (int msk = 0; msk < (1 << n); msk++)
    {
        if (__builtin_popcount(msk) != k)
            continue;
        // Do whatever you want in O(n) time.
    }
}

Where __builtin_popcount(msk) is built-in function returning number of set bits in mask.

One can think that this code runs in O(n22n) time. But in fact all the skips will be made in O(n2n) time as well as the logic of your code.

But if your code inside loop works in constant time (using bit magic, or something else), it's there is no way to avoid masks splitting by their popcount using count sort.

→ Reply
»
10 years ago, # |
← Rev. 3   Vote: I like it +14 Vote: I do not like it

There's a neat little trick to find the lexicographically next bit mask with the same number of bits as a given one, which you can use here:

    inline int next_bit_perm(int v) {
        int t = v | (v - 1);
        return (t + 1) | (((~t & -~t) - 1) >> (__builtin_ctz(v) + 1));
    }
    // ...
    // handle 0 bits separately
    for (int k = 1; k <= n; ++k) {
        for (int w = (1<<k)-1; w < (1<<n); w = next_bit_perm(w)) {
            // do whatever you want with w
        }
    }

In each iteration, this will enumerate the masks with k bits in increasing order, in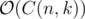 . Be warned though: I have no idea if this is actually fast in practice or just looks cool.

→ Reply